對角互補模型探究
摘要:本文中以2024年江蘇中招數學真題中的對角互補模型問題為例,深入探討對角互補模型相關問題,旨在為學生提供一種有效的解題路徑和策略,幫助學生提高解決此類問題的能力.
關鍵詞:對角互補模型;解題策略;初中數學
對角互補模型是初中數學幾何部分的重要內容之一,它基于角的互補性質,通過構造輔助線、利用相似三角形和全等三角形等方法來解決與補角相關的角度計算和證明問題.這類題目不僅考查學生對角的互補性質的理解,還考查學生的空間想象能力和邏輯推理能力.
1 真題
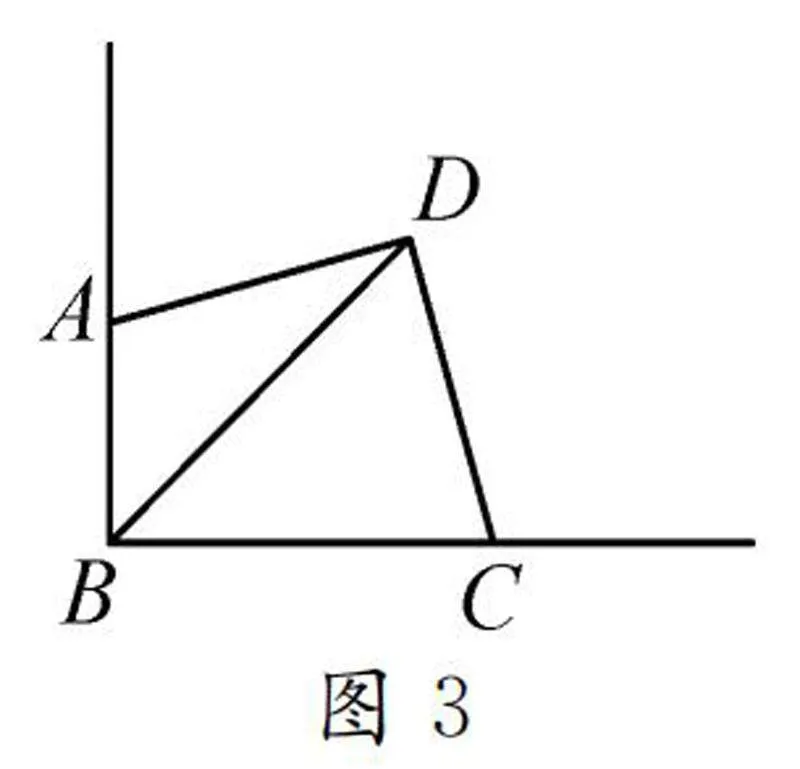
真題1(2024年江蘇鹽城中考數學第16題)如圖1,在△ABC中,∠ACB=90°,AC=BC=22,點D是AC的中點,連接BD,將△BCD繞點B旋轉,得到△BEF.連接CF,當CF∥AB時,CF=______.
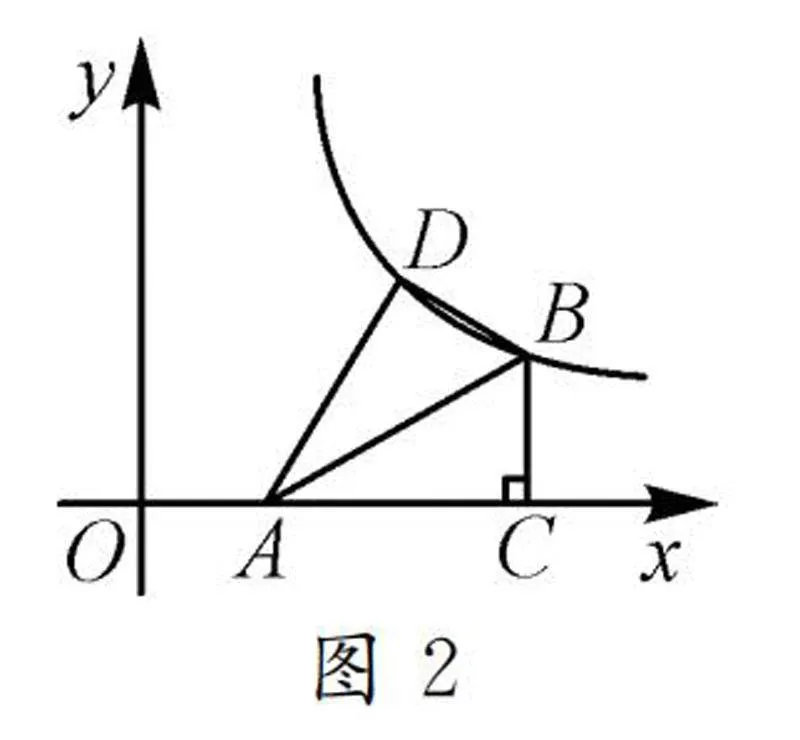
真題2(2024年江蘇揚州中考數學第17題)如圖2,在平面直角坐標系中,點A的坐標為(1,0),點B在反比例函數y=k/x(x>0)的圖象上,BC⊥x軸于點C,∠BAC=30°,將△ABC沿AB翻折,若點C的對應點D落在該反比例函數的圖象上,則k的值為______.
2 對角互補模型的概念、性質及解題策略
對角互補模型特指四邊形內存在一組對角角度之和為180°,同時滿足至少一組鄰邊長度相等的特定幾何形態.此類模型依據角度的特性,主要細分為含有90°和120°角的兩種類型.在解決這類問題時,我們通常會采用兩種主要的輔助線構造方法:一種是通過頂點作雙重垂直線來形成全等的三角形,另一種則是通過圖形的旋轉操作來構建全等的三角形.這兩種方法都能有效地幫助我們理解和解答涉及對角互補模型的問題.
2.1 含90°對角互補模型
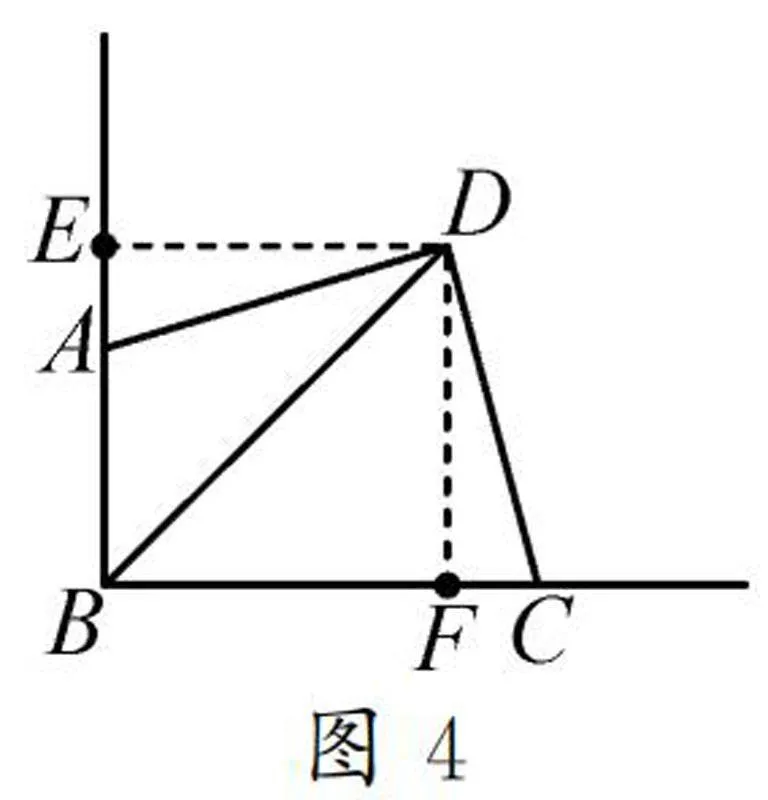
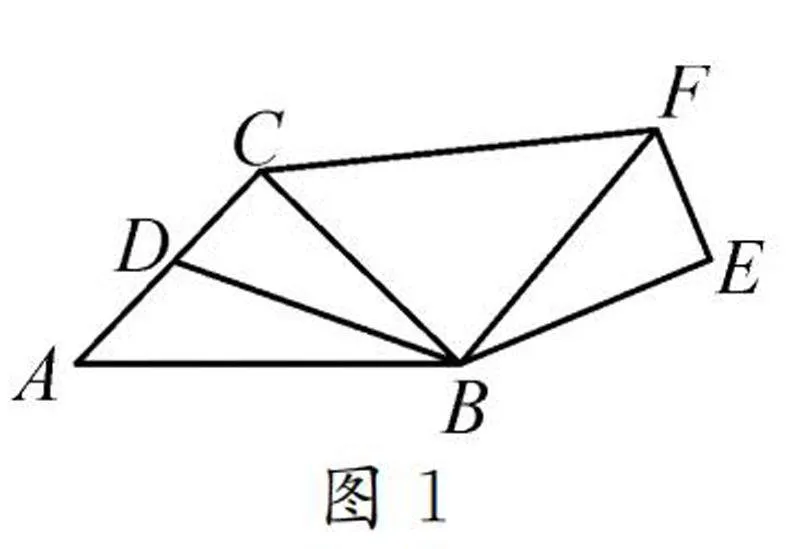
如圖3,已知∠ABC=∠ADC=90°,AD=DC,則可得:①BD平分∠ABC;②AB+BC=2BD;③S=S+S=1/2BD2.
證法一:過頂點作雙垂線證明.
①如圖4所示,過點D作DE⊥EB,DF⊥BC,垂足分別為E,F.
∴∠DEA=∠DFC.
∵∠ABC=∠ADC=90°,
∴∠DAB+∠DCB=180°.
∵∠DAB+∠DAE=180°,
∴∠DCB=∠DAE.
∵AD=DC,
∴△DEA≌△DFC.
∴DE=DF.
∴四邊形DEBF為正方形.
∴∠ABD=∠DBC.
∴BD平分∠ABC.
②∵四邊形DEBF為正方形,
∴BD=2EB=2BF.
③∵△DEA≌△DFC,
∴S=S+S=S+S+S=S=1/2BD2.
證法二:旋轉法證明.
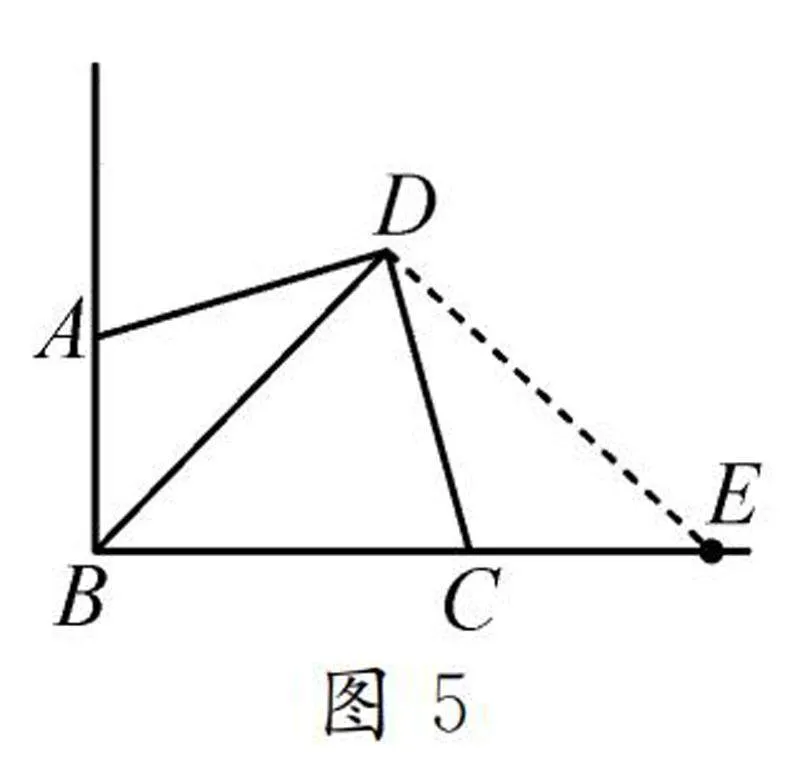
圖5①如圖5,將△DAB繞點D逆時針旋轉,當AD與DC重合時,點B落在射線BC上的點E處.
∴△DAB≌△DCE.
∴∠ADB=∠CDE.
∵∠ADB+∠BDC=90°,
∴∠BDC+∠CDE=90°.
∴∠BDE=90°.
∵DB=DE,
∴△BDE為等腰直角三角形.
∴∠DBC=45°.
∴BD平分∠ABC.
②∵AB=CE,
∴BC+CE=BC+AB=2BD.
③∵△DAB≌△DCE,
∴S=S+S=S+S=S=1/2BD2.
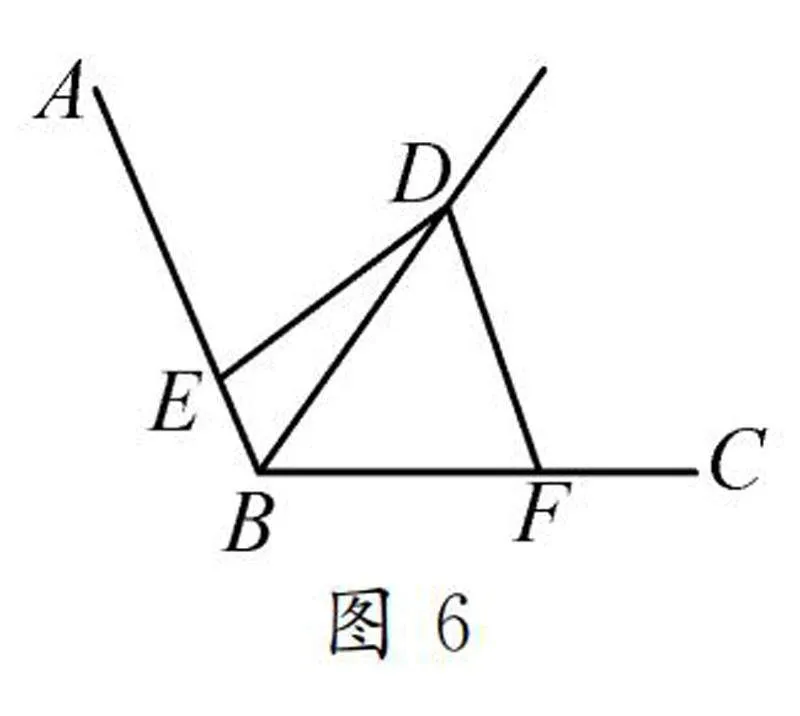
2.2 含120°對角互補模型
如圖6所示,已知∠ABC=2∠EDF=120°,DE=DF.
結論:①BD平分∠ABC;②EB+BF=BD;③S+S=34BD2.
3 對角互補模型復習策略
3.1 基礎知識梳理
為了更有效地復習、掌握對角互補模型,學生需要對相關的基礎知識進行梳理和強化.首先,學生需要深入理解角的互補性質,這是對角互補模型的基本前提.其次,學生應熟練掌握平行線的性質,如平行線間的同旁內角互補、內錯角相等、同位角相等,因為這些性質與對角互補模型有著密切的關系[1].此外,相似三角形和全等三角形判定條件也是復習的要點.因為在對角互補模型的解題過程中,經常需要利用這些判定條件來證明三角形的相似或全等,從而找到解題的突破口.為了更有效地復習這些基礎知識,學生還可以采取制作思維導圖、編寫知識卡片等方式,將知識系統化、條理化,便于記憶和回顧.除了上述的基本知識點,學生還需要對與對角互補模型相關的定理、公式進行系統回顧和整理.例如,勾股定理、三角函數等,這些定理和公式在解決對角互補模型問題時經常會被用到.通過復習這些定理和公式,學生可以更好地理解和應用對角互補模型.
3.2 模型思維訓練
在掌握了基礎知識后,學生應當進行深入的模型思維訓練.這不僅意味著要識別出題目中蘊含的對角互補模型,更要深入理解模型的本質及其所蘊含的幾何規律.通過大量的練習和模擬,學生能夠在腦海中建立起對角互補模型的清晰圖象,提高對這種模型的敏感度.當遇到相關題目時,學生能夠迅速形成條件反射,聯想到對應的模型和解題策略,從而高效、準確地解答問題.這種訓練不僅有助于提高學生的解題速度,還能幫助他們形成更為系統的幾何思維模式[2].
3.3 解題思路內化
解題思路的內化對于提高解題能力至關重要.學生首先需要深入理解并掌握對角互補模型的解題思路和方法,如巧妙地構造輔助線,準確地運用相似三角形和全等三角形的性質等.在解題的過程中,學生應當注重思路的連貫性、條理性,確保每一步都有充分的依據和明確的目的.為了加深理解,學生應不斷進行練習和反思.通過反復實踐、思考,學生可以將這些解題思路、方法逐步內化為自己的思維習慣.這樣,在面對類似的問題時,學生便能迅速并準確地找到解題的切入點,從而提高解題的效率和準確性.這一過程不僅有助于提升學生的數學能力,更能培養學生嚴謹的邏輯思維和自主學習能力[3].
3.4 練習與反饋
練習是提高解題能力的重要途徑.在復習對角互補模型的過程中,學生需要通過大量的練習來加深理解.同時,學生應注重練習的質量和效果,選擇具有代表性的題目進行練習,并及時反饋練習情況.通過練習,學生可以了解自己的不足和需要改進的地方.這時,學生可以向老師請教或與同學交流討論,以獲得更好的指導和建議.在練習過程中,學生還應注重錯題的總結和歸納.通過整理和分析錯題,學生可以找出自己的薄弱環節和易錯點,并制定相應的改進措施.這樣可以幫助學生更好地鞏固知識點和提高解題能力[4].
4 結論
對角互補模型是初中數學幾何部分的重要知識點之一,它涉及角的互補性質、相似三角形、全等三角形的判定條件等多個方面.通過掌握相關的解題方法和策略,學生可以有效地提高解決此類問題的能力.因此,在復習過程中,學生應重視對角互補模型的學習和練習,加強基礎知識的掌握,通過不斷練習提升自己的思維能力和應用能力.
參考文獻:
[1]蘇錫永.淺談數學教學與高階思維能力培養[J].考試周刊,2023(12):69-72.
[2]劉海燕.初中數學建模思想初探[J].現代教育科學,2011(4):126-128.
[3]張細婷.關于中考數學復習方法與策略的探索[J].學周刊,2015(20):198.
[4]呂鳳艷.基于中考導向的初三數學復習課教學探究[J].遼寧教育,2022(1):89-92.

