挖題根尋變式
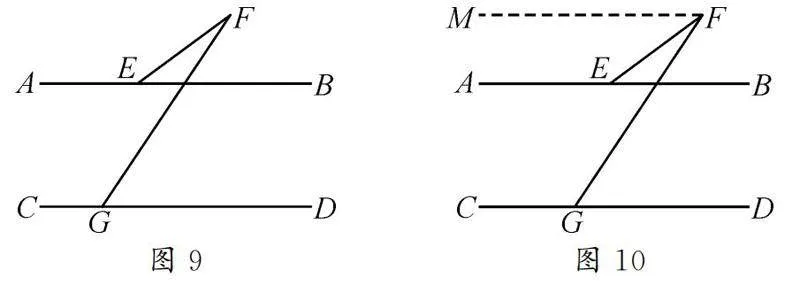
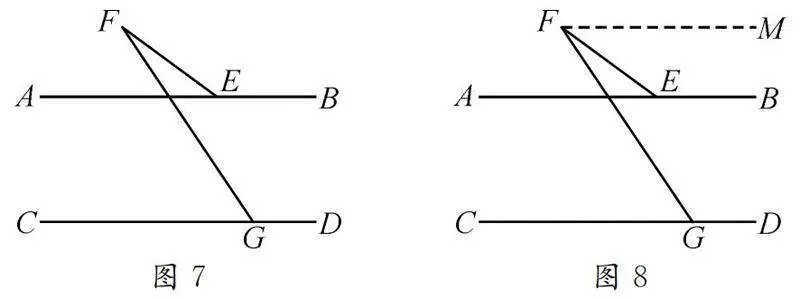

摘要:教師在課堂教學中一定不能就題講題,可適當根據題目的特點進行變式教學,這是新課改實行一段時間后初中數學教師形成的普遍認識.本文中以折線截平行線中角的關系為例,一方面探討教師在課堂實踐中開展變式教學時需遵循的原則及方法,另一方面探究如何從題根出發實現變式.
關鍵詞:題根;變式;折線;平行線
在平行線這一部分內容中,學生時常會遇見折線截平行線的問題,且這類問題的變式特別多.從學生的解決情況來看,教師應對學生加強這方面的訓練.筆者建議使用變式教學法,以不斷激發學生的數學思維.為此,本文中以折線截平行線為例,對如何變式及解題進行研究與分析.
1 變式教學法與變式
變式教學法是一種以變式為主的教學方法,是教師不就題講題、不斷拓展學生思維的重要體現.這需要教師不斷挖題根,然后在題根的基礎上進行變式.
從心理學的角度來看,變式就是將感性的材料通過不同的材料和方法重新進行組織,從而讓學生對概念、方法等產生更深刻的理解[1].在初中數學中,題目的變化形式非常多,可從情境出發,也可從思維出發,還可從知識點出發,總之本質不變而形式與方法多變.另外,在變式時應遵循一定的原則,如導向性原則、啟發性原則、探究性原則和創新性原則.
首先,導向性原則.教學是一種雙向活動,主要參與者是學生和教師,二者圍繞著教學目標開展活動[2].變式是作用于師生活動的方法,對教學目標的完成具有導向性作用,所以,變式需遵循導向性原則.
其次,啟發性原則.教學是教師不斷啟發學生思維的過程.因此,教師在開展變式教學時,一定要精心設計問題情境,讓問題不斷啟發學生的思維,從而幫助學生分析和解決問題.
最后,創新性原則.變式雖然是將題根進行變化,但每個變式都不同于題根,是一種創新.不僅如此,題根在變,解題方法也在變,所以變式也是方法的創新.
2 題根及解法示例
為了說明變式在課堂教學中的實踐,本文中以折線截平行線為例,并將題根示例如下:
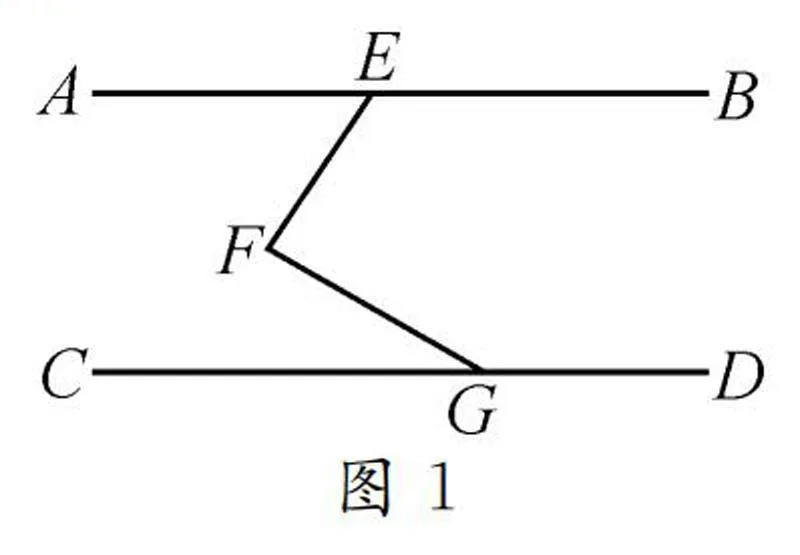
如圖1,AB∥CD,試確定∠DGF,∠EFG,∠FEB之間的數量關系,并說明理由.
分析:由于三個角∠DGF,∠EFG,∠FEB無法構造在一個三角形中,因此應充分發揮AB∥CD這個重要條件的作用.此時,可作兩種輔助線.一是過點F作AB的平行線,二是連接EG.
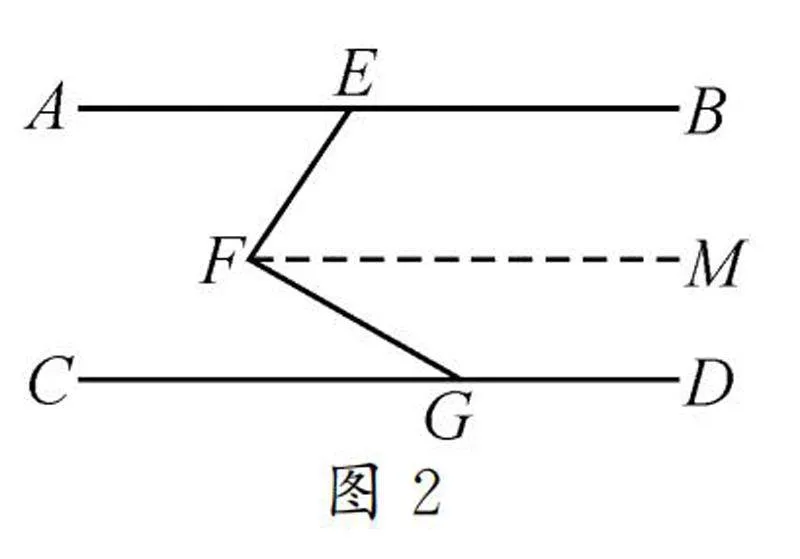
解析:如圖2,過點F作AB的平行線FM.因為AB∥CD,FM∥AB,所以AB∥CD∥FM.由平行線的性質,可得∠BEF+∠EFM=180°,∠MFG+∠DGF=180°.而∠EFG=∠EFM+∠MFG,所以∠DGF+∠EFG+∠FEB=360°.
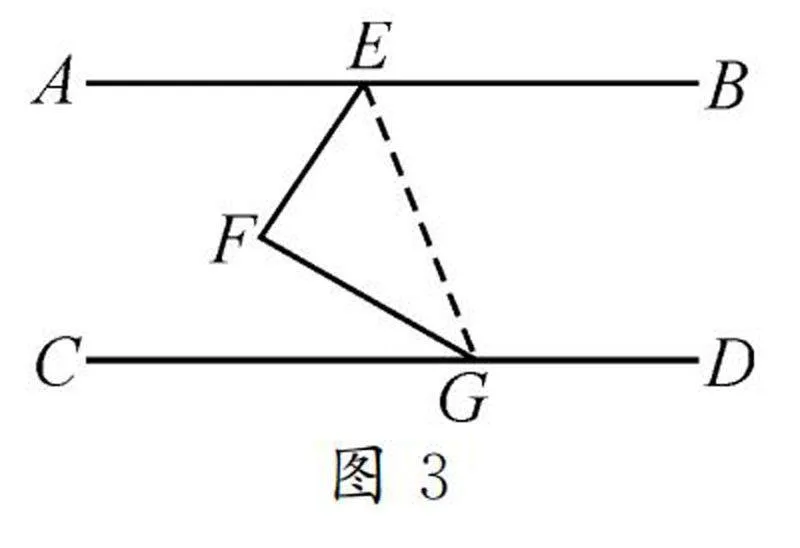
如圖3所示,連接EG.因為AB∥CD,所以∠BEG+∠DGE=180°.因為△EFG內角和是180°,∠BEG+∠FEG=∠FEB,∠EGD+∠EGF=∠DGF,所以∠DGF+∠EFG+∠FEB=360°.
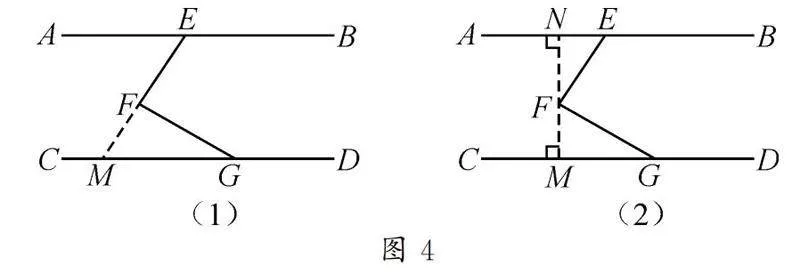
受圖1、圖2兩種作輔助線的方法及兩種不同解題思路的啟發,本題還可作如圖4所示的輔助線,同樣可得到“∠DGF+∠EFG+∠FEB=360°”的結果.
3 根題挖掘
通過分析后發現,上述問題的題根是“給出平行線和折線的位置關系求角之間的數量關系”.于是,在這個題根基礎上,就給出了兩個對象,即兩條互相平行的直線和一條折線,同時給出了一個問題,即求三個角之間的數量關系,考查了平行線的性質、判定等知識.同時,從圖2、圖3兩種不同的解法也可看出,解決這類問題可構造平行線,也可構造三角形.甚至,由此拓展出來的圖4對應的兩種不同解法中,每種方法都綜合了前兩種方法,同樣可達到解題的目的.
由此可得到變式思路,即題根變化、解法變化.首先,變化題根可改變折線的方向,還可將折線的位置由兩平行線中間改為外面.其次,在解法上要求學生盡量一題多解.
4 變式呈現及解析
(1)折線在中間且向右
如圖5所示,AB∥CD,試確定∠DGF,∠EFG,∠FEB之間的數量關系,并說明理由.
解析:如圖6,過點F作AB的平行線,那么AB∥CD∥MF.由平行線的性質,可得∠BEF=∠EFM,∠MFG=∠DGF.而∠EFG=∠EFM+∠MFG,所以∠EFG=∠BEF+∠DGF.
(2)折線在外面且向左
如圖7所示,AB∥CD,試確定∠DGF,∠EFG,∠FEB之間的數量關系,并說明理由.
解析:如圖8,過點F作AB的平行線,那么AB∥CD∥MF.由平行線的性質,可得∠BEF+∠EFM=180°,∠MFG+∠DGF=180°.而∠EFG=∠MFG-∠EFM,所以∠EFG=∠BEF-∠DGF.
(3)折線在外面且向右
如圖9所示,AB∥CD,試確定∠DGF,∠EFG,∠FEB之間的數量關系,并說明理由.
解析:如圖10,過點F作AB的平行線.那么AB∥CD∥MF.由平行線的性質,可得∠BEF=∠EFM,∠MFG=∠DGF.而∠EFG=∠MFG-∠EFM,所以∠EFG=∠DGF-∠BEF.
5 反思與總結
課堂是師生不斷互動的舞臺,所以變式也應該體現出師生互動的過程.為此,筆者認為教師在進行變式或開展變式教學時,應注意以下幾個方面:
首先,課堂活動中的變式教學是師生的雙向活動,教師在變式時一定要圍繞著教學目標進行,應考慮變式是否能幫助教師達到教學目標,是否能幫助學生彌補不足等.
其次,變式教學是為了更加激發學生的思維,讓學生得到更深刻的啟發.因此,在課堂實踐過程中,可讓更多的學生參與到變式討論中.同時在學生討論的過程,教師可收集相關意見,為接下來的變式提供內驅基礎.
最后,變式就是創新,這種創新是否體現在題目改變或解法改變上,都需要教師深刻思考.例如,本文中的三種變式雖然圖形發生了改變,但題目沒有發生改變,方法也沒有發生改變.因此,筆者建議教師應和學生一起就本文中的變式進行更深入的探討或研究.
綜上所述,變式不應局限于條件改變、要求改變,而應深入到解法改變等.只有這樣,變式教學發揮的作用才會愈加明顯,學生的思維才會被更有效、更徹底地激發,對學生的發展才會更有利.
參考文獻:
[1]何珊.變式教學在初中數學“圖形與幾何”教學中的應用研究——以平行線為例[J].數學學習與研究,2022(16):146-148.
[2]莘義成.數學試卷評講課教學策略——以“相交線與平行線”試卷評講課為例[J].中小學數學(初中版),2020(10):56-59.

