以數學背景透視“有理數的乘方”的教學

摘要：利用代數結構的理論和運算間的關系依據，結合指數冪符號發(fā)明的歷史，透視有理數乘方的教學要創(chuàng)設針對性問題情境、規(guī)范概念形成教學、設置創(chuàng)造性練習并將運算納入系統(tǒng)，以達成多元教學目標.

關鍵詞：代數運算；乘方（冪）；教學啟示

教師通過努力，可以實現“要給學生一碗水，自己要有一桶水”.有一分證據說一分話，教師知道的東西越多，上課時的語言就會越運用自如，學生感知信息就不會太費力.一些優(yōu)秀教師教育技巧的提高，正是得益于他們持之以恒的學習，不斷地補充他們“知識的大海”.如果我們依據代數系統(tǒng)的運算和指數冪發(fā)展背景的知識來理解“有理數的乘方”，教學應該更有底氣.

1 代數運算的含義

1.1 加法

1.2 乘法

1.3 乘方、開方的定義

2 乘方（冪）運算及指數冪符號的歷史

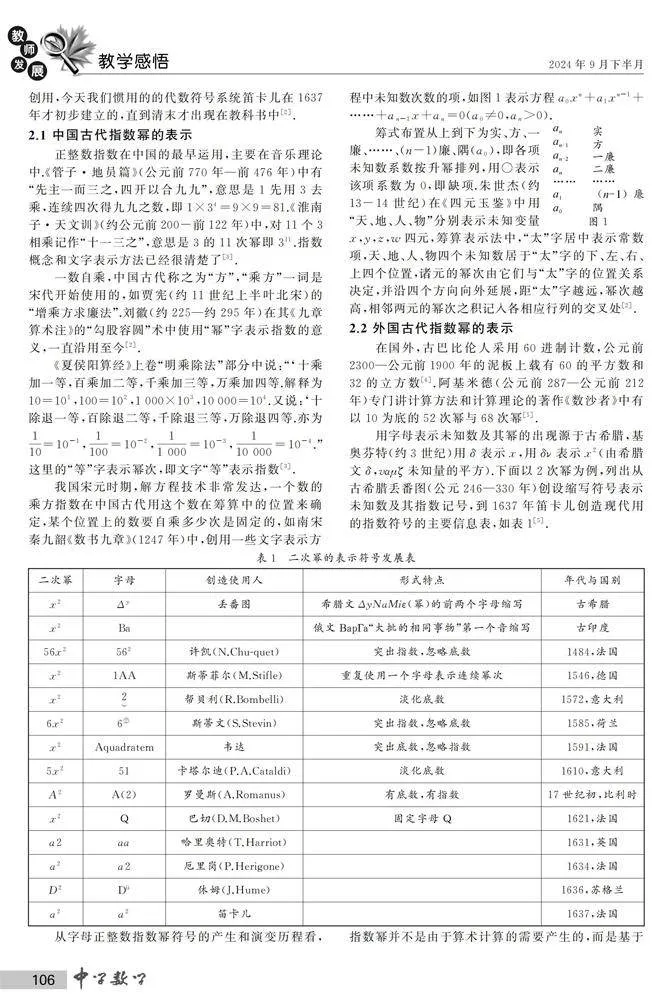
2.1 中國古代指數冪的表示

2.2 外國古代指數冪的表示

3 對“有理數的乘方”教學的啟示

3.1 教學目標宜多元

從代數運算的定義和符號的產生過程來看，本課時教學的基本目標是了解乘方（冪）運算的由來，理解乘方的意義，學習數學思維方法，感受冪表示符號的簡單美，正確計算有理數的乘方.

鑒于《義務教育數學課程標準（2022年版）》在本節(jié)后安排冪的性質及用科學記數法表示數的內容，科學記數法需要10的冪的性質的支撐，而冪的性質是實驗、觀察與思考的產物，是學生數學計算活動的經驗.因本節(jié)課的教學目標不應局限于對乘方意義的理解和運算熟練的“常規(guī)動作”，學生合作探究活動不能“缺席”，對冪的性質的發(fā)現活動應是“自選動作”.唯有這樣才能充分挖掘出這節(jié)課的育人價值，達成課程之效.

3.2 情境與問題要有針對性

3.3 概念的形成需規(guī)范

3.4 乘方練習多創(chuàng)造

運算的定義和具體的計算在數學中一般是兩回事，不管是初等數學還是高等數學都是如此.直接根據定義進行的計算都是基本的，只需達成理解算理的目的.“運算能力主要是指根據法則和運算律進行運算的能力.”[7]為了算得又快又好，計算主要是利用運算法則或性質展開，乘方用乘法來算很簡單，所以教學中不要在此花費太長時間，運算在理解好算理之后為止，過多地強化計算，容易給學生造成乘方運算還是要寫出乘法形式后再計算，乘方沒有什么意義的印象.要盡快地通過運算發(fā)現運算規(guī)律，這是運算的重點.乘方運算的關鍵不在計算上，而是運算性質及作為一個整體的冪在字母底數、字母指數時的運用，以及其能拓展出好的數學知識和方法.

依據代數結構理論，有理數集中有一些特殊元素：0元、單位元1、其負元-1、十進制記數法的10.以這些特殊元素為底數的冪是經常遇到的，2，3的值比較小，以它們作為底數的冪值相對容易計算，也是教學中舉例常用到的，所以應加強這些底數或運算后組合的底數冪的規(guī)律的練習，減輕學生不必要的計算負擔，更好地發(fā)現乘方運算的規(guī)律，挖掘出數學之魅.

3.5 納入系統(tǒng)更完美

數學是“通過對研究對象的符號運算……，形成數學的結論和方法，幫助人們認識、理解和表達現實世界的本質、關系和規(guī)律”[7].乘方運算也是一種代數運算，滿足中學數學中所研究的運算的一般規(guī)律，也需要和其他運算相結合進行綜合運用、混合運算，所以無論從更好地理解乘方運算的意義，引導學生發(fā)現乘方運算性質的角度，還是從綜合進行混合運算的角度，都要將乘方運算納入運算的系統(tǒng)，溝通乘方運算與其他運算的聯系和區(qū)別，采用整體的觀點來看待運算，用更高的觀點來認識、分析問題，采用運算研究的一般規(guī)律和方式方法，結合以前學過的其他運算來理解乘方，遵循運算知識拓展或集合拓展的規(guī)則，為后面開方等運算的研究做好準備，豐富與提升學生對運算的認識，構建數學之諧.

參考文獻：

［1］官運和.初等數學研究[M].北京：清華大學出版社，2017：15-37，55.

［2］傅海倫.中外數學史概論[M].北京：科學出版社，2007：76.

［3］李夢樵.中國古算書簡介五、《張丘建算經》、《夏侯陽算經》[J].中學數學教學，1984（1）：36-38.

［4］VICTOR J.KATZ.數學史通論[M].2版.李文林，鄒建成，胥鳴偉，等，譯.北京：高等教育出版社，2004：5-6.

［5］徐品方，張紅.數學符號史[M].北京：科學出版社，2006：202-212.

［6］波利亞.怎樣解題[M].閻育蘇，譯.北京：科學出版社，1982.

［7］中華人民共和國教育部.義務教育數學課程標準（2022年版）[S].北京：北京師范大學出版社，2022：1，8.