深度學習視角下轉變學生學習方式的課堂教學

摘要：“深度學習-單元教學”的核心思想是實現學生學習方式的轉變.文章結合案例，在一個知識單元內通過整體規劃，設計讓學生學習方式從“學會—會學習—自主學習”轉變的系列課.同樣，在一節課內也可以分層推進，設計活動，實現學生學習方式的轉變.

關鍵詞：深度學習;學習方式;自主學習;教學設計

王尚志教授在對全國教師進行深度學習培訓時指出：“深度學習-單元教學”的核心思想是實現學生學習方式的轉變［1］，即學習方式從“學會”到“會學習”，再到“自主學習”的轉變.課堂學習能夠深度發展的關鍵在于學生的深度參與.為此，教師備課時，要在關注學情、課程標準、知識特點和內容難度等因素下，盡可能地設計有利于學習方式轉變的課堂活動.

1 設計思路

“深度學習-單元教學”作為一個理念，其目的是讓教師在設計課堂教學時，從單元的角度來整體規劃、統籌安排.事實上，在一個單元或一節課內，我們都可以根據知識特點和思維發展過程設計出有助于學生學習方式改變的課堂教學.

1.1 單元內整體規劃

在一個單元內，不同知識之間除了邏輯上的關系外，很多時候在研究方法和內容形式上也是極為相似的，這就使得學生學習方式的轉變成為可能.心理學指出：一個知識或技能的掌握，一般要經過“模仿、訓練和應用”三個階段.這說明初次遇到一個知識時，學生很大程度上是要通過教師的講授才能夠“學會”，再次遇到相似的知識時學生便有了“會學習”的基礎，而第三次出現相似的知識時，學生才有可能會“自主學習”.

案例1 “三角函數”教學的整體規劃

在學習正弦函數的圖象與性質時，筆者以講授式為主展開課堂教學以達到兩個目標：

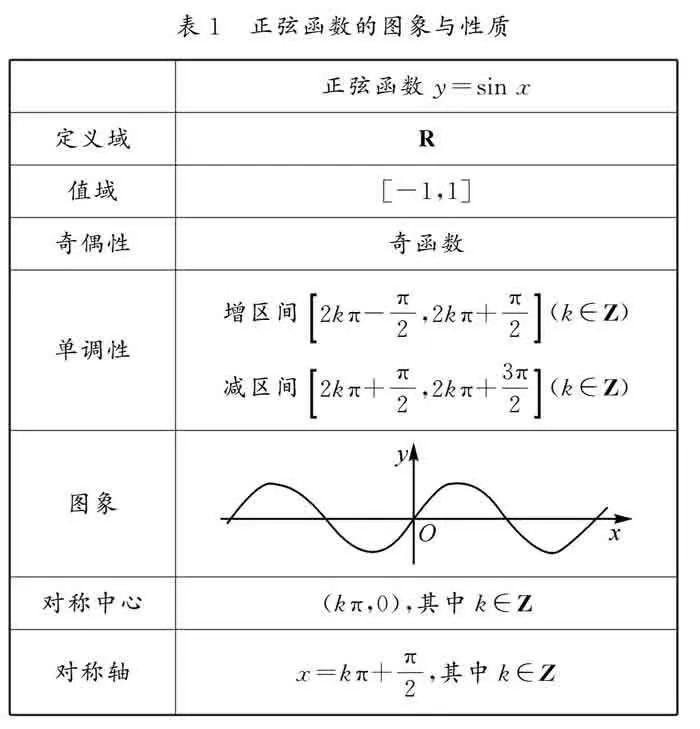
（1）最終通過表格給出正弦函數的定義域、值域、圖象、單調區間等（如表1）；

（2）指出研究函數的一般思路是通過定義和解析式，先給出函數的圖象，之后再研究函數的性質;或者是通過定義和解析式，先得到函數的部分性質，之后研究圖象，最后再繼續研究函數的性質.

此課設計的目的是讓學生在知識和方法上達到“學會”［2］.

隨后，在學習余弦函數的圖象和性質時，筆者先給出余弦函數的定義，隨即當著學生的面擦去上節課表格（表1）中右側的具體內容，保留左側的研究方向，并將表頭從正弦函數改為余弦函數，然后讓學生根據上一節課的研究方法自己探究并試圖完成表格.這節課最終在學生個人研究、小組討論、師生合作的基礎上完成教學過程.此課設計的目的除了掌握知識和方法外，還要讓學生“會學習”.

最后，在學習正切函數的圖象和性質時，因為之前兩節課的鋪墊，所以完全可以在給出正切函數的定義之后，讓學生自主探究，完成學習.

不難看出，上述三節課的設計關注了三角函數章節中知識和方法的銜接，學生思維的螺旋上升，以及學習方式的轉變，即學會—會學習—自主學習.

數學中有很多這樣的知識結構，教師在設計課堂教學時應予以關注.如在立體幾何的學習中，學習線線角、線面角、面面角這三個知識點時，便可以整體規劃，設計出改變學生學習方式的系列課.

1.2 課堂中分層推進

在設計一節課的教學時，由于知識理解的不斷深入和思維的連貫性，我們也需要關注這節課中內容的分層推進，以及學生學習方式的轉變.這也符合皮亞杰認知發展理論中的從“同化”到“順應”的過程.也只有這樣，才能判斷學生是否真正掌握了一個知識.

案例2 “直線與圓錐曲線的位置關系”的教學

在這節課中，筆者按照以下分層推進的三個部分安排學生的學習活動.

首先，筆者采用講授式講解例1，通過本例給出解決此類問題的基本方法.教學中，先通過直線和橢圓聯立得到一元二次方程，然后用判別式來判斷方程解的個數，進而得到直線與橢圓的位置關系，即什么時候有兩個公共點、一個公共點和無公共點（此法簡稱“聯立方程”）.

例1 已知橢圓C：x22+y2=1，斜率為k的直線l經過點A（－2，0）.若直線l與橢圓C有兩個公共點，求k的取值范圍.

然后，筆者給出一個直線與雙曲線位置關系的問題（如例2），讓學生模仿之前的例題先自行解決，繼而師生合作完成教學過程.教學中，所用的解題方法與例1完全相同，所不同的是曲線形式的變化，以及聯立所得的一元二次方程的二次項系數非恒正，需要討論，且在第（2）問的解答中不能只考慮判別式.

例2 已知雙曲線C：3x2－y2=1，斜率為k的直線l經過點M（0，－1）.

（1）若直線l與雙曲線C有且只有一個公共點，求直線l的方程；

（2）設直線l與雙曲線C的左支有兩個公共點，求k的取值范圍.

最后，筆者不給具體的題目，讓學生自己給出直線和拋物線來探究它們的位置關系，并通過匯報交流的形式來完成學習.

此課的三個部分展示了“聯立方程”這個方法的遷移過程：直線與橢圓的位置關系—直線與雙曲線的位置關系—直線與拋物線的位置關系.其中，例1旨在讓學生“學會”基本方法;例2在應用方法的同時增加了思維的深度，旨在讓學生理解知識和方法的本質，并學會學習;而最后則是給出研究目標讓學生“自主學習”，即學生自己給出直線和拋物線來研究問題，這再一次增加了思維的深度和廣度.整個設計層層遞進，達到了有思維深度的知識遷移.

本節課讓學生從不同角度來審視“聯立方程”這個方法，不僅實現了學生的學習方式從“學會—會學習—自主學習”的轉變，還構建了結構化的知識體系.這有助于學生的認知向高水平層次——分析、評價和創造發展（注：教育學家布魯姆在認知領域教育目標分類中將認知由低到高分為六個水平層次，即記憶、理解、應用、分析、評價和創造）.

2 教學實施建議

實現學生學習方式的轉變是一個長期工程，不可能一蹴而就.它不僅與教師的管理方式和教學風格等有關，還受班級氛圍和學生性格等因素影響.具體實施時要關注以下三點.

（1）教師要轉變觀念

教師要認識到學習方式的轉變對學生的長期發展，乃至終身學習都是至關重要的；要認識到短期內的教學進度和學生成績可能會受到影響，但學生的學習興趣和思維品質會逐漸提升；要認識到學生學習方式的改善對教師專業素養和駕馭能力的要求不是下降了，而是提高了；等等.

（2）過程是艱辛的

實現學習方式的轉變，關鍵在于為學生提供自由發揮的學習空間，這就需要教師不斷嘗試，設計出適度開放的學習任務.實施之初，學習活動的自由度和任務的難度需要反復斟酌.只有不斷地實踐和磨合，才能真正實現學生的“自主學習”.這其中尤其要關注開放的學習活動如何讓班級內所有的學生都有所獲.

（3）評價方式多元化

學習方式的轉變將會引起學業表征和認知水平的改變.傳統的評價方式已不能反映學生自主學習所帶來的學習興趣、團隊協作、探究能力等方面的改善.只有從學習態度、參與程度、研學成果等多角度來評價學生的學習活動，才能反映出學生“自主學習”的成效，形成良性循環，促進學習方式的真正轉變.

參考文獻：

［1］王尚志.深度學習-單元教學，深度學習課題全國培訓第一期［R］.北京：課程教材研究所，2021.

［2］課程教材研究所.普通高中數學教科書（B版）必修三［M］.北京：人民教育出版社，2019：36-41.