數形結合思想在小學數學教學中的實踐應用

摘 要：數形結合思想在數學教育領域具有不可替代的核心價值，特別是在小學的數學教學中扮演著極其重要的角色.將數學的抽象概念與形象的圖形緊密結合，不僅加深了學生對數學概念的理解，還提升了他們解決具體問題的能力.本文通過分析具體的教學案例，探討了數形結合思想在小學數學教學中的應用，突出了其在培養學生的數學核心素養中的關鍵作用．

關鍵詞：數形結合思想；小學數學；實踐應用

在數學這一學科領域中，“數字”與“圖形”構成基本的研究元素，它們之間存在著一種辯證的對立統一關系.在小學階段采用數形結合思想的教學方法，可以幫助學生透徹理解數學知識的形成過程，使學生不僅知道各種數學現象的表象，還能洞察其背后的邏輯，從而培養學生深厚的數學認知基礎和運用這種思想的技巧.基于對數形結合思想的理解，學生能夠積極主動地探索數學，將抽象難懂的數學理論轉化為直觀的圖形表示，實現思考的可視化，從而深刻把握數學概念的真正含義.這種思想會激發學生對數學的興趣，有效提升他們的數學思維能力及其核心素養的整體發展．

1 數形結合思想在小學數學中的教學實踐

數形結合思想強調通過數與形的互相轉化和對應關系來解決數學問題.［1］這里的“數”涉及數字、代數式、方程、函數以及數量關系等，它們共同展示了數學的精確性；“形”則指代幾何圖形和函數的圖象，體現了直觀性.

作為一種基本的數學思維方式，數形結合思想在小學數學教育中扮演著不可或缺的角色.它通過結合抽象的數學問題和直觀的圖形幫助學生更深刻地理解和掌握數學概念，從而提升他們的解題技能.［2］本文以“數學廣角——數與形”為案例，探討這一思想在實際教學中的應用．

1.1 課前預習：激發數形結合思想運用意識

在課前準備階段，教師可以通過設計具體問題來激發學生的數形結合意識.［3］例如，在探究連續奇數求和的問題時，教師可引導學生計算“1+3+5+7”的和，并提示他們注意和與特定幾何圖形，如正方形的面積之間的聯系.當學生完成計算后，他們知道算式總和等于16，這正是4的平方，即一個邊長為4的正方形的面積.通過這樣的發現，學生不僅體會到數學的趣味性，同時也能觀察到數學中數與形之間的相互映射和解釋.這種體會能深化學生對數學的興趣和探索欲望．

1.2 課堂探究：提升數形結合思想的運用能力

在課堂互動環節中，教師利用多媒體工具展現的多種圖形不僅可以吸引學生的眼球，也能為他們打開一個直觀的數學世界大門.學生被邀請進行獨立思考，如分析圖中不同顏色的小正方形數量，并探索這些數目與圖形序號之間的關系.通過這種方式，學生逐步發現深灰色和淺灰色正方形數量的規律.學生觀察到隨著圖形序號的增加，深灰色正方形的數量等于序號本身，淺灰色正方形數量則表現為遞增趨勢.這類發現不僅加深了他們對數學規律的理解，也鍛煉了他們對數形結合思想的運用能力.進一步地，通過小組討論，學生之間的互動和合作得到加強.學生在小組內互相啟發，探討分數之和與圖形面積的關系.這種探討幫助他們更全面地理解數形結合的概念.學生可能會發現某個分數序列的和與某種圖形的面積直接相關，這種關聯使得分數累加與圖形面積的相互驗證和解釋成為可能．

1.3 情境創設：生活中數形結合思想的實際應用

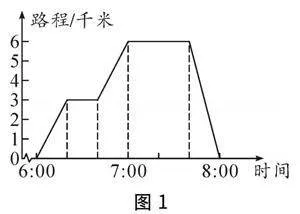
教師可以構建一個緊貼學生日常生活的實例，進一步加強學生在生活中數形結合思想的實際應用能力.例如，小明的爸爸每天清晨跑步前往6千米外的廣場進行鍛煉，請詳細分析小明爸爸的行進路線（如圖1）．

接下來，學生將運用數形結合思想來處理以下幾個問題.

（1）假設小明的爸爸全程未休息（不考慮速度變化），他跑向廣場所需的時間為 分鐘.

（2）小明的爸爸在廣場逗留了 分鐘.

（3）小明的爸爸回家的速度為每小時 千米．

圖形展示了時間與路程的關系.直線與時間軸平行時，表明小明的爸爸停止不動.路程從0到6千米說明他前往廣場，從6千米回到0則表示他歸家.針對問題（1），根據圖示，小明的爸爸早上6點出發，7點到達廣場，整個過程耗時60分鐘.期間有線段平行于時間軸，顯示他休息了20分鐘.若不停歇，實際到廣場的時間為40分鐘.關于問題（2），小明的爸爸7點抵達廣場，7點40分開始返回，故他在廣場的停留時間為40分鐘.從圖中還可以看出，小明的爸爸8點回到家，回程用時20分鐘.通過計算可知，他的返回速度為18千米/時．

1.4 專題訓練：鞏固數形結合思想的應用

在小學數學的專項練習中，教師精選適合的題目，以加強學生數形結合思想的運用技巧.例如，通過對一個大三角形被切分成數個小三角形的分析，學生可以估算出陰影部分所占的比例.這類習題不僅是對學生數形結合思想觀念理解的一種考查，同時也提高了他們使用數學知識來解決實際問題的能力.實際情境與折線圖的結合進一步擴大了數形結合思想的使用范圍，并且讓學生在處理復雜的問題時能更加靈活地運用已學的知識.［4］教師通過這些專項訓練，不僅鞏固了學生的學習成果，還擴展了數形結合思想的實際應用場景，使他們能夠在面對真實世界的問題時，有效地應用數形結合思想．

2 數形結合思想在小學數學教學中的有效應用策略

2.1 “以形助數”在小學數學教學中的應用策略

在小學數學的教學過程中，運用“以形助數”策略顯得尤為關鍵，該策略通過圖形的形象表達幫助學生深刻理解數學的各種概念.利用數線和數軸這些工具，學生可以直觀地了解數字的順序及其相對大小.這不僅使他們對整數有了更加深入的了解，同時也為學習分數和小數提供了實用的視覺輔助.在分數的具體教學中，通過使用直觀的圖形，學生可以更準確地掌握分數的單位和比較分數的大小，進一步加深對數學概念的理解.在探討算法時，教師利用直觀的圖形幫助學生具體理解分數加減運算中的通分過程，讓學生可以形象地把握復雜的計算步驟.在解決具體問題，如植樹問題時，教師運用線段圖分析數據關系，構建數學模型，顯著增強了學生處理這類問題的技能.在統計學的教學中，統計圖的形象展示，不僅簡化了數據處理流程，也增強了學生在數據分析和預測方面的技能.“以形助數”的策略不僅加深了學生對數學概念的理解，也有效提高了他們解決實際問題的能力，為他們的數學學習奠定了堅實的基礎，使得他們在數學的學習之路上更加得心應手．

2.2 “以數解形”在小學數學教學中的應用策略

教學中應用“以數解形”的策略作為解開“圖形與幾何”領域之謎的關鍵，能夠幫助學生通過定量分析深入探究幾何形狀的核心屬性.教師通過運用多感官的教學手段，如模型搭建和實際操作，讓學生在觀察和感覺幾何形狀的同時，通過測量等活動，將這些感知轉換成具體的數據，以此來探討形狀的特征.例如，在學習過程中，學生通過測量線段長度來學習如何用數字描述形狀的屬性，這種方法基礎性地介紹了如何利用數字解釋長方形和三角形的邊角特征以及圓的基本特性等更高級的幾何概念.在進階學習，如圖形的對稱性、平移和旋轉等概念中，學生通過數學的語言來準確描述和分析，不僅提升了對幾何變換的理解，還練習了使用數學工具分析圖形運動的技能.在具體解決問題，如計算長方體體積時，教師會引入小正方體模型，引導學生在構建和計算過程中自行發現體積公式.這種教學方式不僅讓學生經歷數學知識的形成過程，還極大地提高了他們的空間想象力與邏輯推理能力.通過這樣的“以數解形”應用，學生對幾何知識的理解更加深入，為未來的數學學習奠定了堅實的基礎，在數學的世界中更加自如．

2.3 “數形互助”在小學數學教學中的應用策略

“數形互助”的教學方法在小學階段非常有效，這種方法結合了數學中的數字和幾何中的形狀，極大地增強了學生對數學概念的理解和應用能力.教師通過此策略引導學生發現數與形之間的密切關系，使用恰當技巧深入挖掘數學的本質.以“角的種類”為例，利用活動角度器及測量工具，學生可以直接操作感受角度的變化.從0°起始，學生主動調整角度器，直到90°.教師解釋直角及區分銳角和鈍角.當角度增至180°，平角的概念被介紹，360°的完整圓周角則標志著角度分類的結束.這種互動和實踐的教學模式不僅幫助學生直觀理解角度的大小及其分類，也使他們能夠將幾何形狀與數值緊密結合，建立起完整的數學理念.

2.4 加強指導，培養學生的作圖能力

在小學數學的課程中，提高學生的作圖能力是實現數學與幾何結合教學目的的關鍵所在.因此，教師需要仔細策劃教學活動，確保使用的圖形既標準又能精準表示數與形之間的關系，防止學生對圖形知識的誤解.因而，教師必須有計劃地提高學生的作圖能力，指導他們如何準確繪制線段圖、平面幾何圖形、三維圖形及比例圖等，這些能力對于將數學概念具象化非常關鍵.教師通過有效的示范和指導，可以幫助學生形成正確的作圖習慣，并教授他們如何根據具體題目的需求選擇合適的圖形以輔助思考和解決問題.這樣的繪圖訓練使學生能夠將抽象的數學概念直觀地轉換為具體的圖形表達，加深他們對數學原理的理解，從而提高解題效率.總體來說，通過

加強學生的作圖能力的培養，教師不僅幫助學生更有效地掌握數學知識，還能激發他們的創造性和想象力，調動學生主動學習數學知識的熱情．

3 結語

數形結合思想的教學策略突破了傳統教學的界限，成為培養學生綜合能力的關鍵手段.面對數形結合思想的教學需求，教師應不斷探索這一策略在新環境下的應用，調整和完善教學方法，以適應教育領域的不斷變化.隨著教育實踐的創新，數形結合思想的教學將在小學數學教育中發揮更加核心的作用，為學生的全面發展和終身學習奠定堅實的基礎．

參考文獻

［1］于亞群.數形結合思想在小學數學教學中的應用研究［J］.華夏教師，2024（15）：55-57．

［2］付小玲.淺析數形結合思想在小學數學教學中的應用［J］.甘肅教育研究，2024（7）：142-145．

［3］趙晶.“數形結合”思想在小學數學教學中的實踐探究［J］.數學大世界（下旬），2024（4）：53-55．

［4］張登妹.數形結合思想在小學數學教學中的應用研究［J］.教師，2024（7）：48-50．