逆向思維在初中數學解題中的應用

【摘要】在初中數學解題中，當學生無法運用正向思維解決問題時，教師便可以讓學生嘗試從逆向角度看待問題，以降低解題的難度。鑒于此，簡述逆向思維應用在初中數學解題中的意義，并從創設情境、重視例題、逆向拓展、專題訓練、逆用法則五個方面入手，探究逆向思維應用在初中數學解題中的策略，旨在提高學生解題的正確率。

【關鍵詞】初中數學；逆向思維；解題教學

作者簡介：戴正勇（1980—），男，江蘇省鎮江市揚中市新壩中學。

數學思維的培養是初中數學教學的重要目標之一，逆向思維的應用則是解決數學問題的重要方法。初中生正處于從形象思維向抽象思維過渡的關鍵時期，逆向思維的培養能助力初中生發展思維能力，學會靈活應用數學知識。因此，在實際教學中，教師應借助情境、例題等資源，為學生創造更多鍛煉逆向思維的機會，提高學生解決問題的能力。

一、初中數學解題中應用逆向思維的意義

（一）有助于培養學生解題思維

在初中數學學習中運用逆向思維有助于學生解題思維的形成。教師通過需要運用逆向思維的教學活動，可以讓學生掌握多種解題方法，拓展解題思路。久而久之，學生可以養成從不同視角思考問題的習慣，使逆向思維能力和解題水平得到提升［1］。

（二）有助于引導學生理解概念

概念是學生解決數學問題的基礎，也是教師開展具體教學活動的依據。學生對概念的掌握情況會影響學生思維的發散。這就需要教師提高對概念教學的重視程度，利用多樣化教學手段，助力學生對概念形成正確的認知。當前的初中數學教學對學生思維的廣度、深度有較高的要求。學生若僅憑正向思維，且沒有經歷辯證、推導的過程，是很難深入理解數學概念的［2］。對此，教師通過設計解題教學活動，鍛煉學生逆向思維，能使學生對數學概念形成深層次理解，有效拓展知識面。

（三）有助于發展學生邏輯思維

初中數學學科中有一些知識點具有互逆性，如勾股定理及其逆定理、平行線的判定與性質等等。教師講評相關的例題和習題時，鼓勵學生多維度思考數學問題，培養逆向思維能力，并靈活運用公式、定理解決問題，能使學生打破思維定式，促進學生邏輯思維能力的發展。

二、初中數學解題中應用逆向思維的策略

（一）創設情境，培養逆向思考意識

許多初中數學例題和習題蘊含著豐富的生活元素，這為逆向思維的培養提供了足夠的支持，有效彌補了傳統解題教學的不足。在教學中，教師應通過創設情境的方式與學生展開互動，激發學生的探究興趣［3］。教師可以立足于情境，引導學生從相反的角度展開思考。如此一來，學生能夠在教師的引導下發散思維，學會運用逆向思維思考問題、解決問題。

以蘇科版數學八年級下冊“9.4 矩形、菱形、正方形”教學為例，為了讓學生理解矩形、菱形、正方形等特殊的平行四邊形的定義和性質，教師在課堂中借助情境，培養學生逆向思考的意識。首先，教師在教學初始利用討論法，讓學生回答“誰能說一說平行四邊形的定義是什么？平行四邊形有哪些性質？”等問題，旨在幫助學生復習舊知，同時為新知學習奠定良好基礎。其次，教師利用課件呈現矩形、菱形、正方形，并提問：“這三種圖形是平行四邊形嗎？它們的特點是什么？如何定義這三種圖形？”對此，學生在觀察圖形的基礎上，利用平行四邊形的定義和性質逆向驗證矩形、菱形、正方形的特點，使用學過的關于邊、角的知識給出矩形、菱形、正方形的定義。最后，教師引導學生借助逆向思維探究如下問題：有一天，明明小朋友在幼兒園的手工課上看到材料中有一張平行四邊形紙片，就拿起彩筆給紙片的一角涂上了綠色，涂完后因為對自己的作品不滿意，所以想撕去一部分。如果手工課的后續環節還需要用到平行四邊形紙片，那么你認為明明如何撕能既使紙片的形狀仍為平行四邊形，又能使自己的作品有創意？學生便根據平行四邊形的定義和性質，找出解決問題的方法。在上述案例中，教師通過設置具體的情境，能引導學生對問題進行逆向思考，結合所學知識去分析和解決，從而深化對特殊的平行四邊形的認識。

（二）重視例題，逆用數學公式解題

學生進行數學計算時，往往需要代入公式，而這容易使其形成思維定式。為了避免該情況出現，教師應通過逆用數學公式的方式，讓學生在解決問題時理解公式的推導過程。在實際教學中，教師可以以教材例題為基礎，在使復雜問題簡單化的同時，指導學生結合數量關系進行逆推，轉換解題視角［4］。

以蘇科版數學七年級上冊“2.3 絕對值與相反數”教學為例，為了加深學生對絕對值概念的理解，教師在分析教材中的例題后創編如下習題，旨在鍛煉學生的逆向思維：若化簡|1-x|-|x-4|的結果為2x-5，求x的取值范圍。教師發現，很多學生看完該習題后，第一反應是把絕對值去掉，而化簡后仍無法求出x的取值范圍。實際上，該習題不適合運用正向思維解答。對此，教師指導學生結合絕對值的概念逆向思考，進而推測出“1-x≤0”“x-4≤0”這兩個條件，得到x的取值范圍是1≤x≤4。這有助于學生在后續思考中，學會逆用數學公式解答題目，掌握類似問題的解法。

（三）逆向拓展，幫助學生理清思路

解題思路是學生運用數學知識和技能解決問題的關鍵，更是學生數學思維發展狀況的具體表現。培養學生逆向思維能幫助學生理清解題思路，拓展學生思維的廣度、深度，提高學生的解題能力。因此，教師可以從“突破教學重難點”“求解幾何證明題”兩個方面入手進行逆向拓展。

1.突破教學重難點，深入理解知識

在初中數學解題教學中引導學生應用逆向思維，讓學生經歷知識的形成過程，能突破教學重難點，提高學生的理解能力和創造能力。

以蘇科版數學八年級上冊“3.2勾股定理的逆定理”教學為例，考慮到勾股定理的逆定理是學生需要學習的重難點知識，因此教師在解題教學中結合學情，設計以下關于三角形的難度適中的問題，旨在讓學生在用逆向思維解題的過程中，深入理解知識：有一個三角形的邊長分別是a、b、c，且它的邊長與實數n（n＞0）有著a=2n+1、b=2n2+2n、c=2n2+2n+1的關系。請試著證明這個三角形是直角三角形。學生若借助正向思維，圍繞已知條件展開思考，往往在短時間內找不到解題思路；而若運用逆向思維，由問題逆推條件，在看到問題中的“直角三角形”后則會聯想到勾股定理。對此，教師指導學生思考若這個三角形是直角三角形，則這個三角形的三邊有怎樣的關系，進而讓學生找到解題的關鍵所在，即a2+b2=4n4+8n3+8n2+4n+1=c2，得出這個三角形是直角三角形。

2.求解幾何證明題，簡化解題過程

幾何證明題是初中數學學科中的常見題型。而對于一些難度較大的幾何證明題，如果利用正向思維解題，所需的步驟往往較多，解題過程較為復雜，且容易出現錯誤。對此，教師應指導學生從證明的結果入手，逆向分析解題所需的條件，尋找更簡便的解題方法。

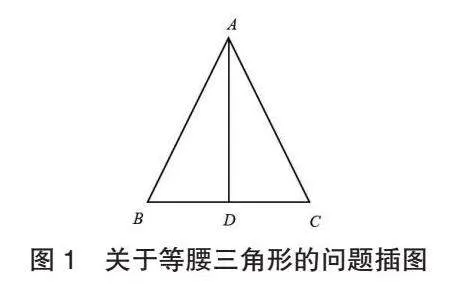
以蘇科版數學八年級上冊“2.5等腰三角形的軸對稱性”教學為例，教師在講解三線合一的定理時展示以下這道幾何證明題，旨在引導學生逆向推導定理，幫助學生掌握相關解法：如圖1所示，已知△ABC中，BD=CD， AD⊥BC，求證AB=AC，∠BAD=∠CAD。在求解這一問題時，教師讓學生先觀察AD在三角形中的地位，明白AD是三角形的中線，也是三角形的高線，三角形的中線和高線重合；然后根據三線合一的定理，判斷出AD還是三角形的頂角平分線；最后根據全等三角形判定定理，得出△ADB≌△ADC，AB=AC，∠BAD=∠CAD。在上述案例中，學生層層遞進地展開逆向思考，發現了結論與問題之間的聯系，得出了對應的結論，順利解決了問題。

（四）專題訓練，提供解題新思路

在以往的學習中，部分學生在練習環節習慣根據條件推導結論。這部分學生的思維方式不利于教師取得理想的教學效果。同時，也有一些學生在解答關于函數圖像、幾何圖形的題目的過程中，容易遺漏題目中的隱含條件，無法順利解題。對此，教師應設計專題訓練活動，指導學生按照新的思路解題。

以蘇科版數學九年級下冊“6.4探索三角形相似的條件”教學為例，為了幫助學生突破思維定式，教師開展需要運用逆向思維的專題訓練活動。首先，教師利用課件展示以下問題：如圖2所示，已知△ABC中，D為AC上的一點，P為AB上的一點，AB=12，AC=8，AD=6，請問AP長度為多少時△ADP和△ABC相似？其次，教師給予學生充足的時間去思考和解題，并鼓勵學生分享解題思路，從中了解到不少學生的解題過程很煩瑣。最后，教師結合學生在解題中出現的錯誤進行講評，在講評時應用倒推法啟發學生思考，若要使△ADP和△ABC相似，需要滿足哪些條件，再讓學生回顧相似三角形的判定與性質的相關知識，進而發現本題存在△ADP∽△ABC、△ADP∽△ACB 兩種情況，應該進行分類討論。在上述案例中，教師引導學生通過逆推形成正確的解題思路，能讓學生在解題時明確圖形與文字之間的聯系，發展學生的數學思維。

（五）逆用法則，學會進行逆運算

逆向思維與逆運算有著密切的關系。教師應通過教學活動培養學生進行逆運算的能力，并在學生展開逆向思考時，給予一定的指導和啟發。教師可以在學生解題的過程中引導學生逆用法則，利用科學的手段培養學生逆向思維能力［5］。

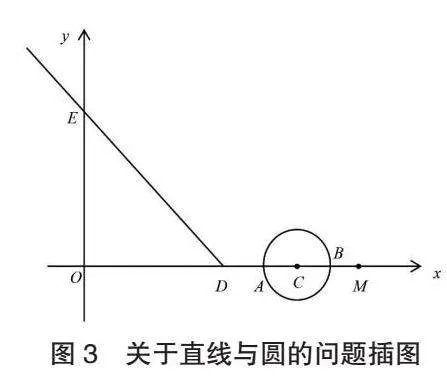
以蘇科版數學九年級上冊“2.5 直線與圓的位置關系”教學為例，對于其中涉及的多個法則、定理，教師抓住時機，為學生創造鍛煉能力的機會。首先，教師在講解知識點時，讓學生思考“直線與圓存在幾種位置關系？”這一問題，為學生進行逆運算奠定良好的基礎。其次，教師借助以下這道考查對直線與圓的位置關系的相關法則的逆用的習題，旨在讓學生嘗試運用逆向思維：如圖3所示，已知DE是一條與x軸和y軸相交的射線，其中點D坐標為（3，0），點E坐標為（0，4）。可移動的點C將從點M出發，以每秒1個單位長度的速度沿著x軸向左做勻速運動，運動的時間為t秒。以點C為圓心、以t個單位長度為半徑的⊙C與x軸交于A、B兩點。當⊙C與射線DE有公共點時，求t的取值范圍。在學生讀懂題意后，教師引導學生思考在點C運動的過程中，⊙C的半徑怎樣變化，⊙C什么時候開始與射線DE有公共點，到什么時候不再與射線DE有公共點。學生通過分析圖3蘊含的信息，發現⊙C在A、D兩點重合時開始與射線DE有公共點，在點C運動到⊙C與射線DE相切的位置后不再與射線DE有公共點。最后，教師要求學生針對問題和圖3的內容，以畫圖的方式驗證逆向推導出的結論，以此在鍛煉自身進行逆運算的能力的同時，深入理解直線與圓的位置變化情況。

結語

總的來說，教師引導學生將逆向思維應用在初中數學解題中，對發展學生數學思維和解題能力有著重要意義。在實際教學中，教師應通過多樣化的方式和手段，為學生營造良好的學習氛圍，讓學生從新的角度展開思考，幫助學生正確地解題，從而增強學生對數學知識的運用能力，實現學生全面發展。

【參考文獻】

［1］翟悅涵.逆向思維、出其不意：反證法在初中數學解題中的應用［J］.中學數學，2023（24）：68-70.

［2］帥仁雷.逆向思維在初中數學解題教學中的運用［J］.數學學習與研究，2023（35）：117-119.

［3］李維龍.基于邏輯推理培養的初中數學教學策略［J］.數理天地（初中版），2023（23）：90-92.

［4］魏小清，李永樹.一個幾何逆定理的證明及應用［J］.數理化學習（初中版），2023（12）：8-11.

［5］薛艷.打破定勢 不走尋常路：例談“逆向思維”在初中數學解題教學中的應用［J］.讀寫算，2023（33）：36-37，91.