一道課本習題的探究

一、習題及其解

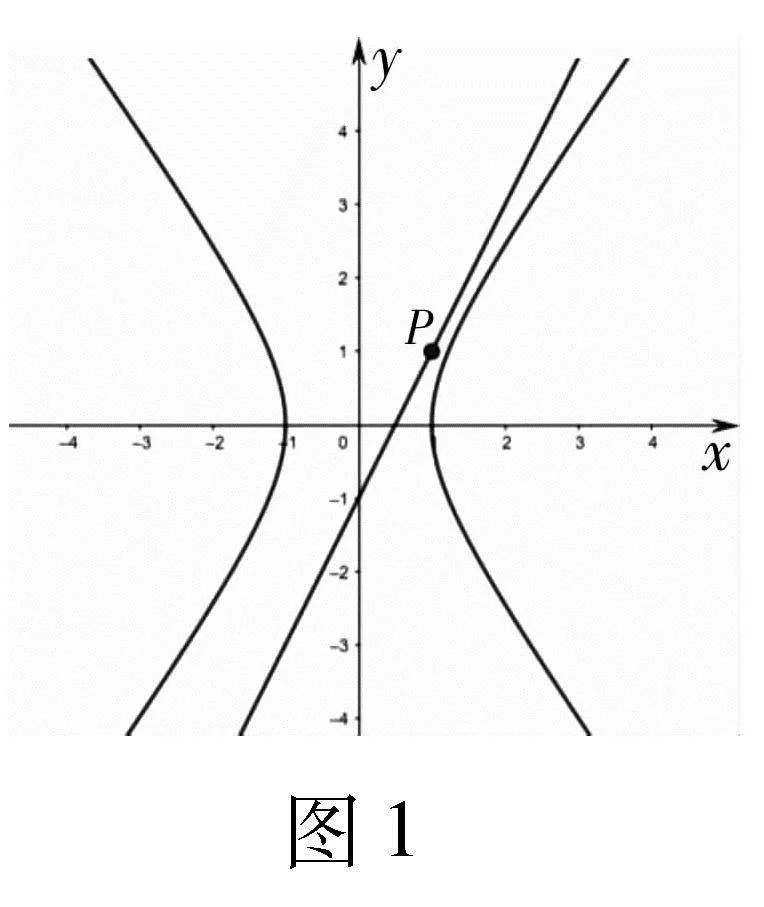
分析：中點弦問題，可使用點差法解決，避免復(fù)雜的運算．當直線l垂直x軸時，可得直線l方程，經(jīng)檢驗不符合題意；當直線l不垂直x軸時，設(shè)A（x1，y1），B（x2，y2），利用點差法，假設(shè)點P（1，1）為線段AB的中點，可得直線l的斜率，進而可得直線l的方程，與雙曲線聯(lián)立，判別式Δlt;0，方程無解，l不存在，綜合即可得答案．

綜上，點P不能是線段AB的中點．

二、習題探究

探究1 為什么直線方程求出來以后，需要與雙曲線方程聯(lián)立，驗證直線與雙曲線是否相交？

這是因為點差法的不等價性．使用點差法的時候，是假設(shè)P為線段AB中點，從而得到x1+x2=2，y1+y2=2，而這個假設(shè)可能會不成立，存在不確定性，所以求出直線方程后需要與雙曲線方程聯(lián)立驗證是否相交．

探究2 之前學(xué)習橢圓的時候，也有類似的利用點差法解決中點弦問題，當時卻沒有強調(diào)驗證相交的問題，利用點差法解決橢圓的中點弦問題需要驗證嗎？

探究3 不用根的判別式，是否有其他方法可以判定直線l不存在？

下面再證明結(jié)論1：

B，且P是線段AB的中點．

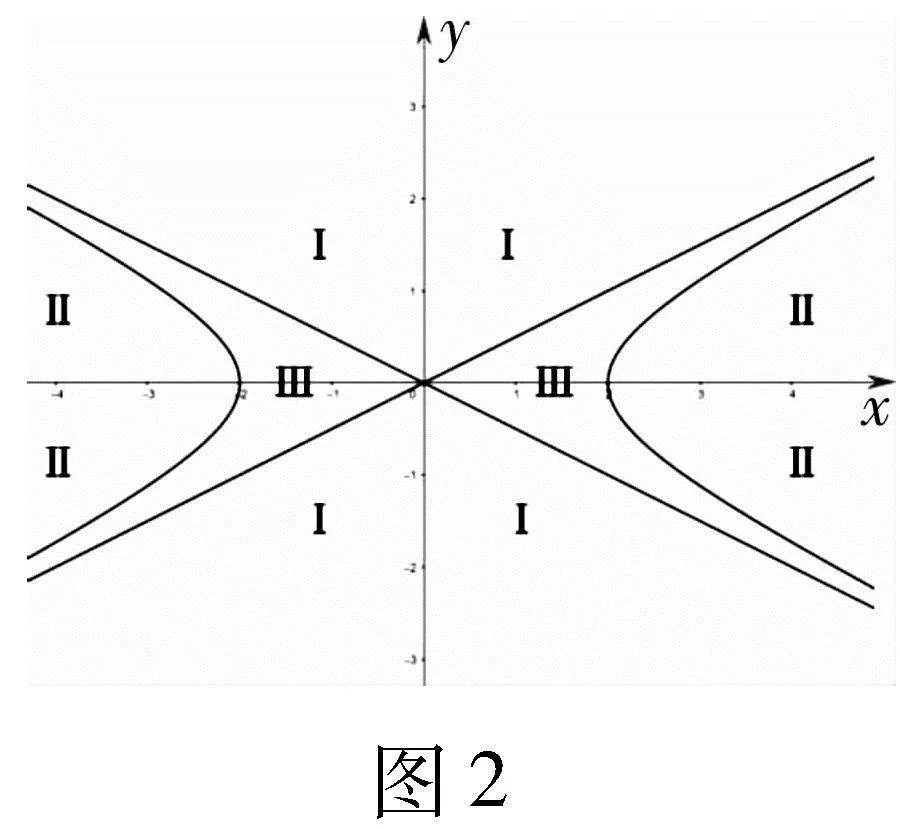
（3）當x0gt;0且y0gt;0時，此時P在第一象限，三個區(qū)域分別討論：

（4）利用對稱性，易得P在第二、第三、第四象限時，在對應(yīng)的區(qū)域Ⅰ及區(qū)域Ⅱ，都存在直線l，使得P是線段AB的中點，在對應(yīng)的區(qū)域Ⅲ，都不存在直線l，使得P是線段AB的中點．

綜上所述，結(jié)論1成立．

三、變式練習

利用上述結(jié)論，可以快速判斷某個點作為中點作直線與雙曲線是否相交的問題．

A．0，2 B．－1，2 C．1，1 D．1，4

參考文獻

［1］ 章建躍，李增滬．普通高中教科書數(shù)學(xué)選擇性必修第一冊［M］．北京：人民教育出版社，2020：128.