聚焦應用“算兩次”法解題

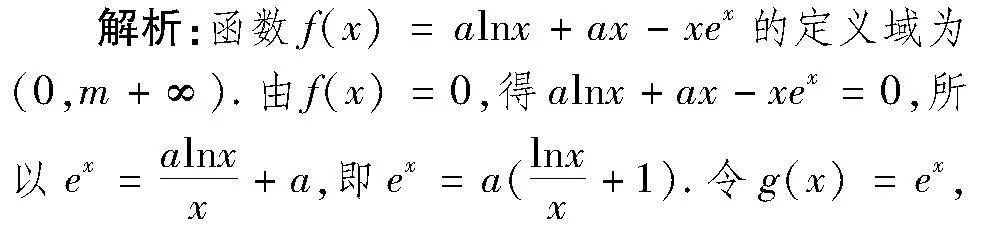
“算兩次”是一種基本的數學方法，其思想就是把同一個量從兩個不同角度計算“兩次”，進而建立等量關系.單墫教授將“算兩次”法的解題形式其比喻成“三步舞曲”，即從兩個方面考慮一個適當量，“一方面…，另一方面…，綜合起來可得…”.“算兩次”法蘊含了化歸轉化和方程思想的運用，在數學問題的諸多方面都有廣泛的應用.下面從幾個方面舉例說明“算兩次”法在數學解題中的應用.

例1 （2022屆陜西省咸陽市二模理11）已知a∈（e，+∞），則函數f（x）=alnx+ax-xex的零點個數為（）.

A.0 B.1 C.2 D.3

點評：利用導數研究函數的性質確定兩個函數g（x）和h（x）的凸凹性，由兩個函數的圖象在點P（x0，y0）處有公切線時應用“算兩次”法列方程求得a=e，然后當a＞e時，由h（x）的圖象在公切線附近向上伸展，從而根據兩函數的凸凹性確定出函數f（x）必有兩零點.

例2 （2023屆湖北省七市州3月聯考18）設數列an的前n數項和為Sn，已知a1=1，2nan-2Sn=n2-n，n∈N*.

（1）求證：數列{an}是等差數列；

點評：（2）在求解Rn的過程中，應用“算兩次”法兩次運用錯位相減法求解的.

例3 （2018年高考江蘇卷13）在△ABC中，角A，B，C所對的邊分別為a，b，c，∠ABC=120°，∠ABC的平分線交AC于點D，且BD=1，則4a+c的最小值為．

點評：利用內角平分線的性質，把一個大三角形面積和分割為兩個小三角形面積之和這兩個角度應用“算兩次”法得到a、c的關系后，通過進行1的代換利用均值不等式求解.

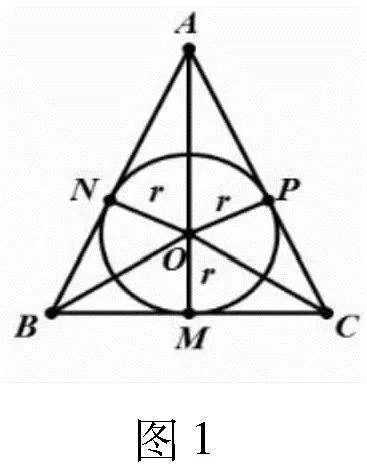
例4 （2020年全國Ⅲ卷理15）已知圓錐的底面半徑為1，母線長為3，則該圓錐內半徑最大的球的體積為．

點評：本題通過作出軸截面，把空間圖形問題轉化為平面圖形問題，然后應用“算兩次”法分別表示S△ABC后，建立等量關系求解.

點評：根據條件作出輔助線，然后應用“算兩次”法求出比例式后得出為的角平分線和為的角平分線，最后結合平面幾何知識推導證明的.