數學解題要善于發掘“特征”

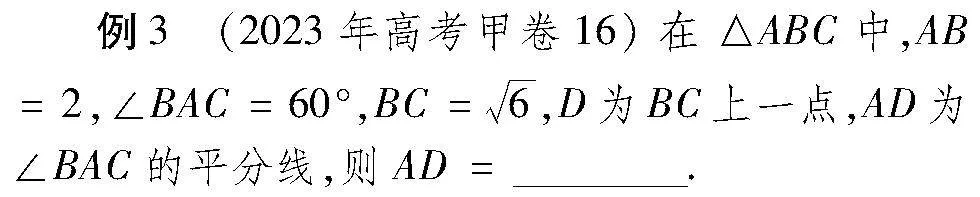
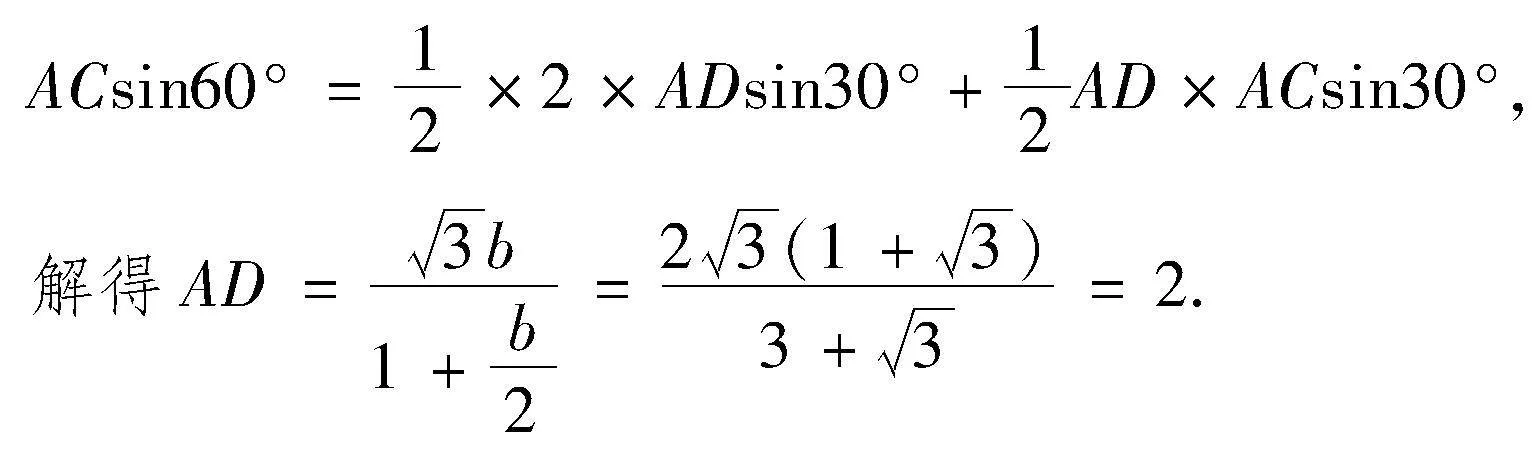
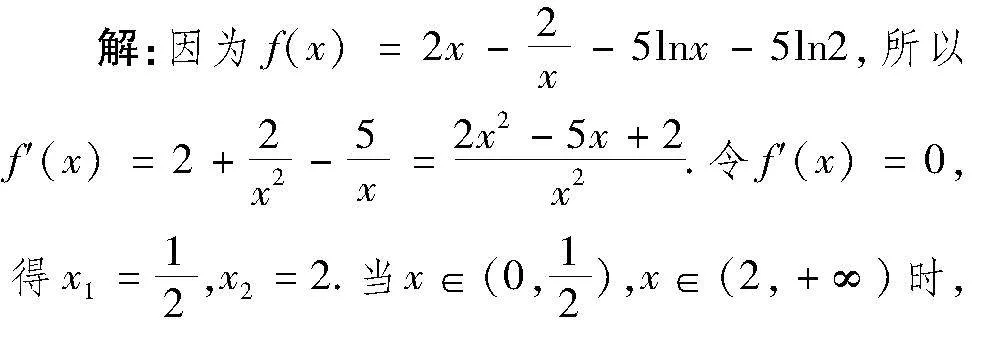
在許多的數學問題中，常常顯示出或隱含著某些“特征”，這些“特征”是問題的題眼，是解決問題的入手點.數學解題中善于發掘這些“特征”，既可以提高解題思路決策的敏捷性，也能使題目的解決過程得到優化，從而起到“四兩撥千斤”的解題效果.本文從幾個方面闡述善于發掘“特征”在數學解題中的應用.

1.數值“特征”

在數學題目中，那些具有某些“特征”的數值，會對解題起著導向作用.從這些特殊數值中展開聯想，并順藤摸瓜去尋找解題途徑，則能使題目獲得新穎、獨創的解法.

點評：本題是“積式型”三角函數計算求值問題，根據角之間的二倍關系“特征”，可運用正弦二倍角公式求解.

2.圖形“特征”

對于一些數量關系的題目，若挖掘或運用其蘊含的圖形“特征”，將抽象、復雜的數量關系轉換為直觀的圖形來求解，從圖形“特征”中尋找解題途徑，則思路直觀、清晰.

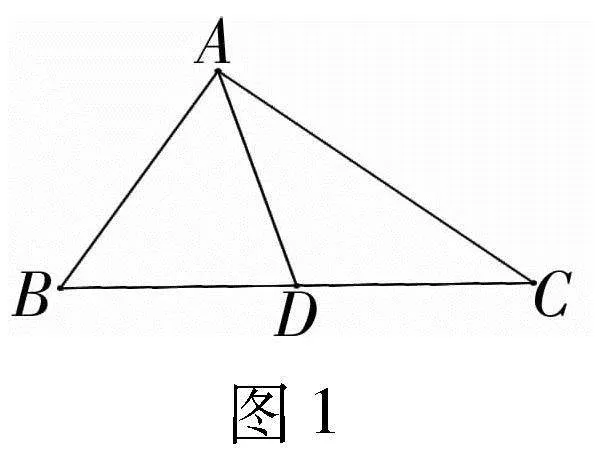
分析：在△ABC中，由AD為∠BAC的平分線，得到∠BAD=∠CAD=30°，然后利用等積法求解.

點評：該解法根據角平分線的“特征”，運用面積相等和兩邊及夾角正弦的面積公式求解，思路清晰，過程十分簡捷.

例4 （2022年新高考Ⅰ卷15）若曲線y=（x+a）ex有兩條過坐標原點的切線，則a的取值范圍是．

分析：設出切點橫坐標x0，利用導數的幾何意義求得切線方程，根據切線經過原點這一位置“特征”得到關于x0的方程，根據此方程應有兩個不等實根，求得a的取值范圍.

點評：利用“切線”求參數的范圍是“切線”問題的逆向應用.本題通過求導數，確定得到切線斜率的表達式，進而表示出切線方程，根據切線過原點這一“特征”，將點的坐標代入切線方程，最后利用判別式求得參數的取值范圍.

3.結構“特征”

一些題目的結構往往能起到“窗口”作用，著眼于對題目結構的觀察、分析并以此作為解題入手點，則能迅速尋找到解題的途徑.

點評：在應用均值不等式求函數或代數式的最值時，有時不一定恰好能用上均值不等式，因此還必須對所給的函數或代數式進行變形整理，通過“拆、拼、湊”等技巧的使用（一般是配湊出“和”或者“積”為定值）構造出均值不等式的形式再進行求解.

4.差異“特征”

數學解題的過程，從一定意義上講，就是實現從題設到結論的推證過程過渡，而識別題設與結論或量與量之間的差異“特征”，則能幫助我們尋找解題途徑.

分析：由于x1為任意量，x2為存在量，從量與量的這一差異“特征”中我們可以認識到需要把題目轉化方可奏效.

點評：本題根據“任意量”和“存在量”的差異關系“特征”，由此把條件不等式恒成立等價轉化為函數間的最值關系，利用導數研究函數的最值及二次函數的最值求解的.