雙切線 雙視角 雙拓展

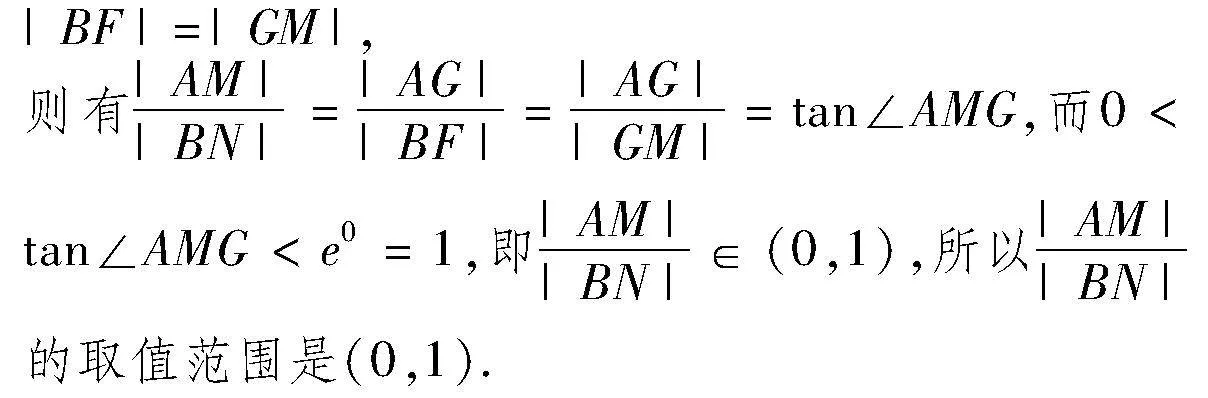
函數切線問題一直是高考中比較頻繁出現的一個基本考點，考查題型往往涉及切線方程的要素確定與求解、參數值的求解或取值范圍的確定、切線條數的判定以及兩條切線的位置關系等相關問題．本文結合一道高考題加以說明.

1．真題呈現與剖析

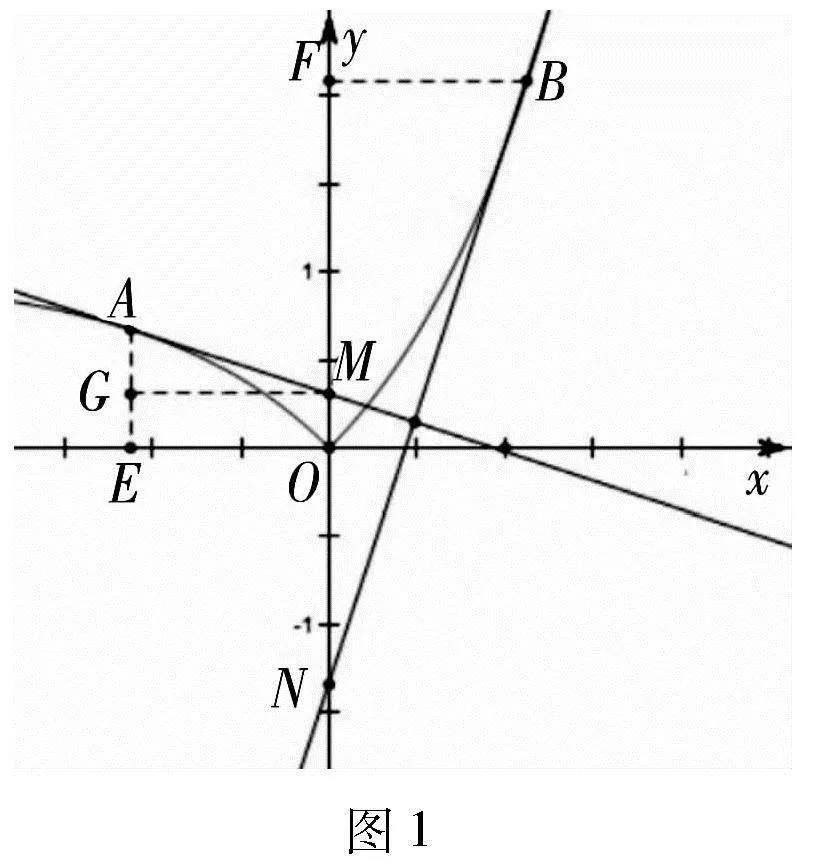
該題以含有絕對值的指數型函數為問題背景，以一個分段函數所對應圖象的兩部分分別作切線，形成“一（函數）拖二（段圖象）”形式，結合過圖象上兩點的切線互相垂直并分別與y軸確定相應的交點，建立這兩點與y軸上交點的連線，求解所確定的線段長度的比值的取值范圍．本題巧妙融合函數與導數之間的相關知識，有“數”有“形”，有“動”有“靜”，是一道新穎性強、融合度高的創新題．

具體破解時，可以從代數視角切入，借助代數運算與邏輯推理進行分析；也可以從幾何視角切入，借助數形結合與邏輯推理進行分析．不同思維視角切入，而破解的關鍵就是抓住導數的幾何意義，建立兩切線垂直關系所對應的參數值之間的關系，進而或代數運算，或幾何直觀，巧妙推理，合理辨析，正確破解．

2．真題破解

評注：方法1通過參數的正負取值情況以及對應的函數解析式，分別求導，利用導數的幾何意義確定相應的切線斜率，結合兩切線互相垂直建立有關斜率的關系式，進而確定參數之間的關系，結合弦長公式的應用來轉化相應的比值關系，結合參數的消元處理，利用變量的取值情況確定對應比值的取值范圍．而方法2主要是利用函數圖象的數形結合處理，通過直角三角形的相似的性質應用，以及直線的斜率定義，結合函數圖象的特征來確定對應角的正切值的取值范圍，即為對應比值的取值范圍．

3．變式拓展

探究1 通過改變函數的解析式，化指數型函數為對數型函數，以及交點所在的坐標軸，其他條件保留不變，得到新的一個變式問題．

探究2 改變問題的設置角度，從同一點出發作指數函數的兩條切線，進而確定相關代數式之間的關系．

變式2 （2021年新高考Ⅰ卷第7題）若過點（a，b）可以作曲線y=ex的兩條切線，則（）.

A．eb＜aB．ea＜bC．0＜a＜ebD．0＜b＜ea

解析：由于函數y=ex是定義域R上的增函數，導函數y′=ex＞0恒成立，設切點為（t，et），則切線方程為y=et（x－t）+et，則有b=et（a－t）+et，整理可得（t－a－1）et+b=0，構造函數f（t）=（t－a－1）et+b，求導可得f′（t）=（t－a）et，由f′（t）=0解得t=a，則知當t∈（－∞，a）時函數f（t）單調遞減，當t∈（a，+∞）時函數f（t）單調遞增，而由題意可知，f（t）=0有兩解，所以f（t）min=f（a）=－ea+blt;0，即blt;ea；又因為當t→+∞時，f（t）→+∞，則存在x1∈（a，+∞），使得f（x1）=0，而當t→－∞時，f（t）→b，則應有bgt;0，此時存在x2∈（－∞，a），使得f（x2）=0.綜上可得0lt;blt;ea，故選D．

4．教學啟示

解決相應的單切線問題，主要是利用導數的幾何意義，借助曲線在切點（x0，y0）處的斜率k=f′（x0）來展開，可以很好地解決一些涉及切點坐標、切線斜率、切線方程、參數值以及相關應用問題等．單切線的破解關鍵就是進行求導運算，并建立關系式k=f′（x0）．而解決相應的多切線問題，也是在利用導數的幾何意義的基礎上，借助其中一條切線方程的設置或求解，再與另一條切線建立題目條件情境的關系式，進而加以分析與應用．破解的關鍵就是從給定的曲線入手，建立關系，合理串聯，巧妙轉化．