例析模長與共軛的關系在強基復數中的考查
2024-12-31 00:00:00何可
中學數學研究 2024年8期




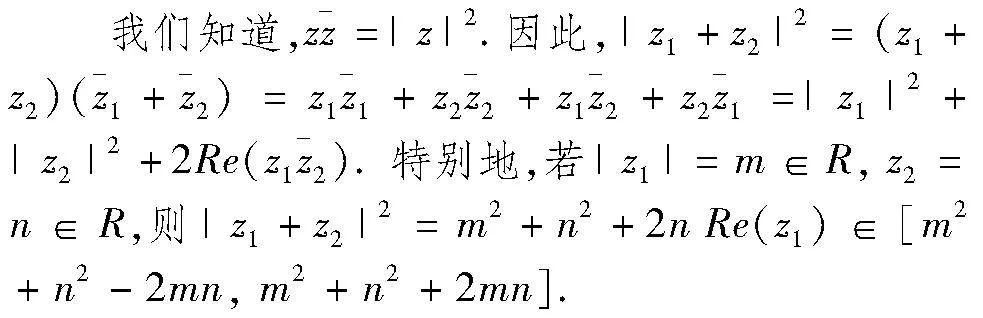

本文例舉模長與共軛的關系在近年強基真題中的考查及應用.
例1(2019北大寒假學堂)已知復數z滿足|z|=1,且z17+z=1,則z=().
解:由z17+z=1,得z17=1-z.兩邊同時取模,得|z|17=|1-z|,從而|1-
評注:例1及變式均需建立模長與共軛的關系,完成相應的計算與證明.
例2(2022清華強基)已知復數|z|=1,求|(z-2)(z+1)2|的最大值.
變式1 (2021清華自強)已知復數z滿足|z|=1,求|z3-z+2|的最值.
評注:本題為復數的單位根為切入點,反復使用模長與共軛的關系來消元與降低次數,最后再通過韋達定理整體代入,求出定值,為一道難度較高的綜合題.
強基計劃對接高校數學專業,旨在選拔基礎學科拔尖創新人才并加以持續培養.又由于復數是后續學習《復變函數》的基礎,因而強基校測對復數要求較高,尤其是模長與共軛的關系更是高頻出現,值得我們去認真研究.

