溯其源 追其本 悟其道

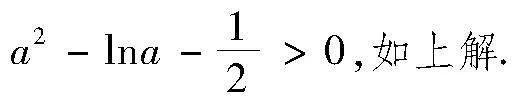
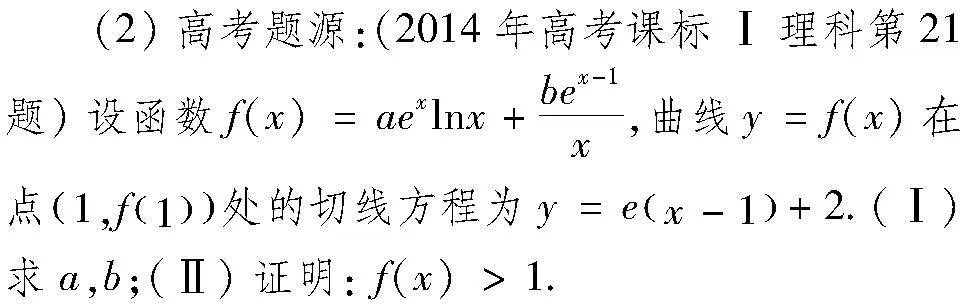
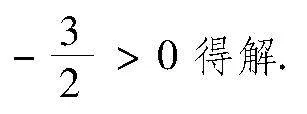
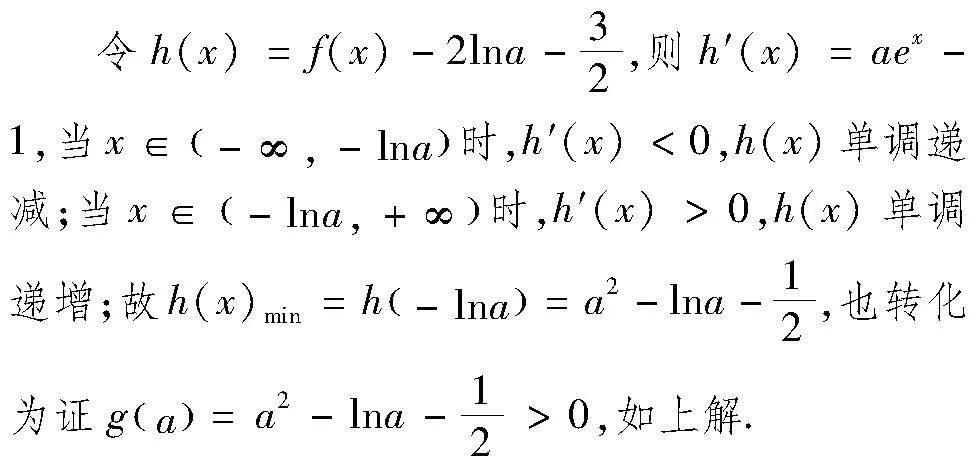
1.試題呈現

題目 （2023年全國數學新高考Ⅰ卷第19題）已知函數f（x）=aex+a－x.

（1）討論f（x）的單調性;

2.試題溯源

（1）課本題源：（人教版選擇性必修第二冊P99綜合運用12題）

利用函數的單調性，證明下列不等式，并通過函數圖象直觀驗證：（1）ex＞1+x，x≠0;（2）lnx＜x＜ex，x＞0.

（人教版選擇性必修第二冊P104拓廣探索18題）已知函數f（x）=ex-ln（x+m）.當m≤2時，求證f（x）＞0.

（3）競賽題源：（2019年全國高中數學聯賽（福建省賽區）預賽）已知f（x）=ex，（1）當x≥0時，不等式x－1f（x）≥mx2－1恒成立，求m的取值范圍.（2）求證：當xgt;0時，f（x）gt;4lnx+8－8ln2.

3.試題探究

第（1）問是考查函數的單調性，需要先對函數求導，再進行分類討論：

f（x）的定義域為R，f′（x）=aex－1，當a≤0時， f′（x）lt;0，f（x）在R上單調遞減；當agt;0時，令 f′（x）=0，得x=－lna，所以，當x∈－∞，－lna時，f′（x）lt;0，f（x）在（－∞，－lna）上單調遞減；當x∈－lna，+∞時，f′（x）gt;0，f（x）在－lna，+∞上單調遞增.綜上，當a≤0時， f（x）在R上單調遞減；當agt;0時，f（x）在－∞，－lna上單調遞減，－lna，+∞上單調遞增.

第（ 2） 問是多元變量導數不等式證明，用導數證明不等式問題一般要通過構造函數，利用函數單調性來證明，其求解可以改變不等式結構，進行恰當的放縮處理，重新構造函數證明不等式.就本題解題思路探究如下：

3.1 橫向探究

思路1：本題是有關證明f（x）gt;k的題型，關于x的函數，先求出f（x）的最小值.

思路2：移項構造新函數g（x），求出新函數g（x）的最小值.

評注：把函數不等式的證明轉化為利用導數研究函數的最值，構造差函數的證法是函數不等式證明中最常規的方法.

思路3：局部位置放縮處理，重新構造函數證明不等式處理.

評注：利用切線不等式ex≥x+1（當且僅當x=0時取到等號）進行放縮處理.

評注：利用切線不等式lnx≤x－1（當且僅當x=1時取到等號）進行放縮處理.

評注：本解法借助同構法與兩個切線不等式lnx≤x－1，ex≥x+1同時進行放縮處理，體現轉化與化歸思想，也體現了微積分中以直代曲，無限逼近的思想.

3.2 縱向探究

研究中可嘗試從多角度對本題進行改編探究.

探究一：改變參數a的位置

已知函數f（x）=eax+a－x.

（1）討論f（x）的單調性;

探究二：改變背景函數

已知函數f（x）=alnx+a－x.

（1）討論f（x）的單調性;

探究三：加入三角元素

已知函數f（x）=ex－a－1x+cosx－2，證明：當a≤1，xgt;0時，f（x）gt;0.

簡解：f′（x）=ex－a+1－sinx≥e0－a+1－sinx=1－a+1－sinx≥0，f（x）單調遞增，f（x）gt;f0=e0－a－1·0+cos0－2=0.

3.3 逆向探究

受上述探究的啟發，我們還可對上述題型進行逆向探究，即對導數恒成立求參數范圍的一類問題進行研究，例如，

例1 （2017年全國Ⅱ卷文科第21題節選）已知函數f（x）=1－x2ex.（1）略;（2）當x≥0時，f（x）≤ax+1，求a的取值范圍.

例2 （2022年全國新高考Ⅱ卷第22題節選）已知函數f（x）=xeax－ex.（1）略;（2）當xgt;0時，f（x）lt;－1，求a的取值范圍.

例3 （2020年全國新高考Ⅰ卷第21題節選）已知函數f（x）=aex－1－lnx+lna.

（1）略;（2）若f（x）≥1，求a的取值范圍.

對導數恒成立求參數范圍問題，可采用通過分離參數、數形結合、變更主元、放縮法、端點效應、必要性探路等方法進行小結和歸類，并對多種方法混合運用破解以上實例.

4. 感悟反思

一道好的數學試題，應立足于考查考生的關鍵能力和數學學科核心素養.2023年全國新高考Ⅰ卷第19題其命題立意深刻、設計新穎，具有典型性、示范性、引領性，是教學研究的良好素材.教學中要善于研究高考試題命題的背景與意圖，從教材例題、習題以及往年的高考題、競賽試題中找到原型，通過對高考試題的多角度探究，尋找試題的命制本源和解法本源，挖掘數學本質，通過改變不同的數學問題情境，并達到靈活應用，從而有效落實數學學科的核心素養培育，實現解決一道題收獲一系列題的學習目的.

參考文獻

［1］李加軍．2022年高考北京卷導數試題的背景溯源、解析和推廣［J］．數學通訊，2022（24）.

［2］王波.借助導數破解含參不等式問題 ［J］.中學數學研究（江西師大），2020（10） .

［3］閆二路，何百惠.函數與導數問題的本質：以2021年全國新高考Ⅰ卷壓軸題為例［J］.中學數學教學，2021（6）.

［4］鄭鍵鴻，田艷玲.增強問題探究意識，提高數學解題能力——對一道高考題的探究、推廣與反思［J］.中學數學教學參考，2020（13）.