例析幾道數學高考模擬創新題

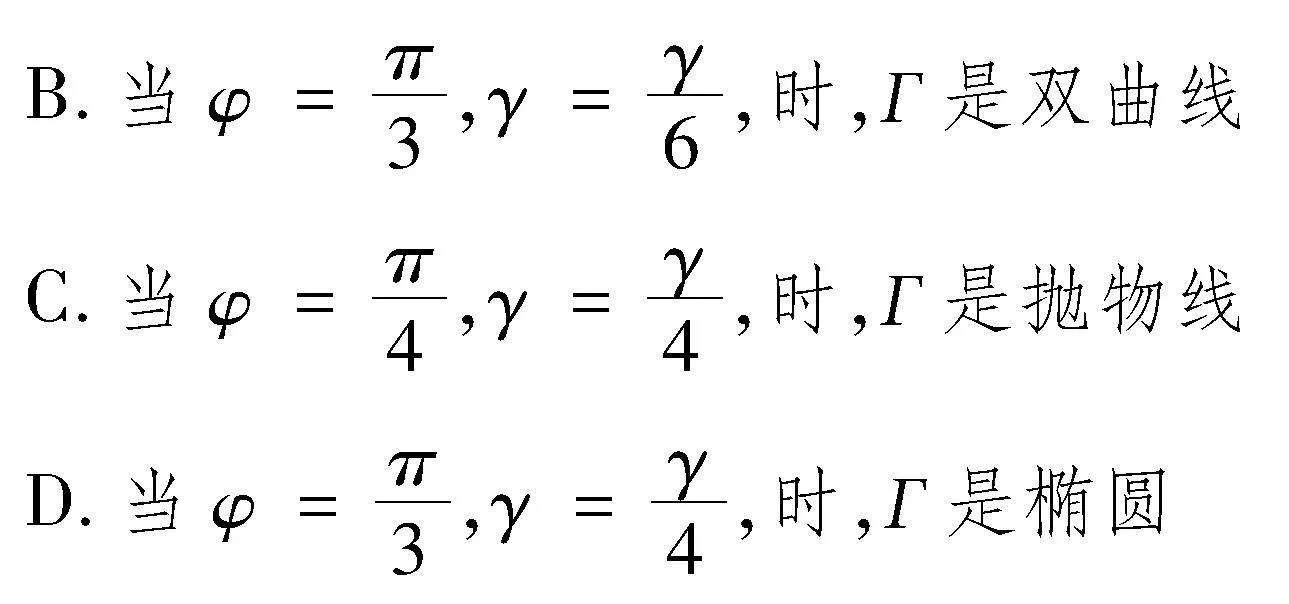
高考數學命題注重創新.在近年高考或各地模擬考試中，出現了許多結構新穎、情境鮮活、“非同尋常”的創新命題，很好地考查了考生在新的信息、背景和設問等命題形式下，靈活運用所學的知識和方法，獨立地分析、思考和探索，進而圓滿解答問題的能力.本文擷取并分類解析出現在近年各地模擬考試中的創新題型，供參考.

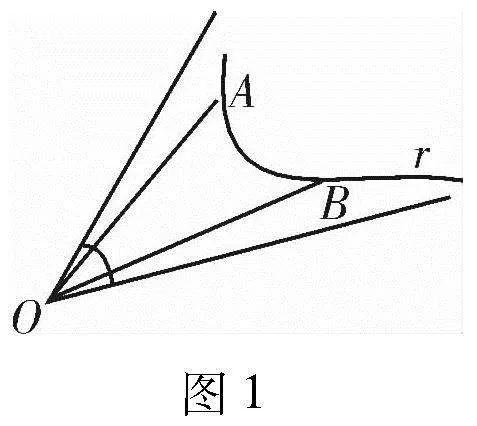
例1（2023屆淮北市一模7）如圖1，對于Г線所在平面內的點O，若存在以O為頂點的角α，使得對于曲線Г上的任意兩個不同的點A，B恒有∠AOB≤α成立，則稱角α為曲線Г的相對于點O的“界角”，并稱其中最小的“界角”為曲線Г的相對于點O的“確界角”.已知

點評：本題首先給出“界角”、“確界角”新定義，在理解新定義的基礎上，通過分析曲線解析式的特點和性質，利用導數的幾何意義和向量夾角公式求解，在考查新定義信息遷移的同時，考查數學抽象、邏輯推理、直觀想象等核心素養及創新思維能力，新穎別致.

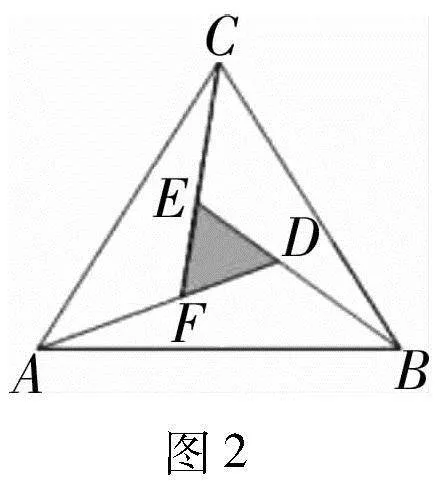
點評：本題以三角形的“圖形拼接”為載體，考查了識圖能力及正、余弦定理和三角形面積公式的應用.

例3 （2024屆“Fiddie學派”高考一模13）1995年，安德魯·懷爾斯成功證明了費馬大定理：當整數n＞2時，方程an+bn=cn沒有正整數解.而早在18世紀，數學家歐拉就證明了費馬大定理中的情形.某同學想尋找情形的簡單證明，即證“方程a3+b3=c3沒有正整數解”.他的證明過程為：若存在正整數a，b，c使得a3+b3=c3，

則a3=c3-b3①，所以a3=（c-b）（c2+cb+b2）②.

因為a＜a2，并且c-b≤c2+cb+b2，所以a=c-b并且a2=c2+cb+b2③.消掉a，可得（c-b）2=c2+cb+b2④.于是c2-2ab+b2=c2+cb+b2⑤.所以3cb=0，從而b=0或c=0，這與b，c都是正整數矛盾⑥.

綜上，方程a3+b3=c3沒有正整數解.

該名同學的證明過程（填“正確”或“錯誤”），如果你認為證明過程錯誤，首個錯誤步驟的序號是（如果第一個填了“正確”，無需作答第二個空）.

解析：步驟①只進行了移項，沒有問題；步驟②只運用了立方差公式，也沒有問題；步驟③存在問題，首先根據a≤a2，c-b＜c≤c2＜c2+cb+b2，并不能推出a=c-b并且a2=c2+cb+b2.這里其實我們也無法給出一個具體的反例，因為由費馬大定理可知不存在正整數a，b，c使a3+b3=c3.由于注意到，若c-b=1，則b≥1，c≥2，于是a2=c2+cb+b2≥4+2+1=7，因此a≥2，這時是不可能有a=c-b的，所以步驟③是錯誤的.故第一空填錯誤；第二空填③.

點評：本題給出一種比較新穎的命題模式——從證明過程中找出錯誤，很好地考查了考生的邏輯推理及數學思辨能力.

A.15 B.31 C.63 D.127

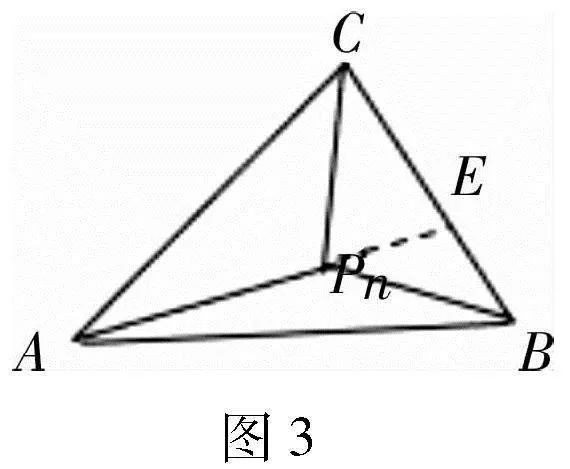
點評：本題將數列遞推關系滲透在向量的分解關系中，運用向量知識得到數列遞推公式后轉化求解，是一道數列與向量有機結合的試題，頗為新穎.

點評：本題創新試題的設問形式，根據復數的代數形式的運算和復數模的公式化簡題設條件，確定a，b的關系后，由此作出判斷的.

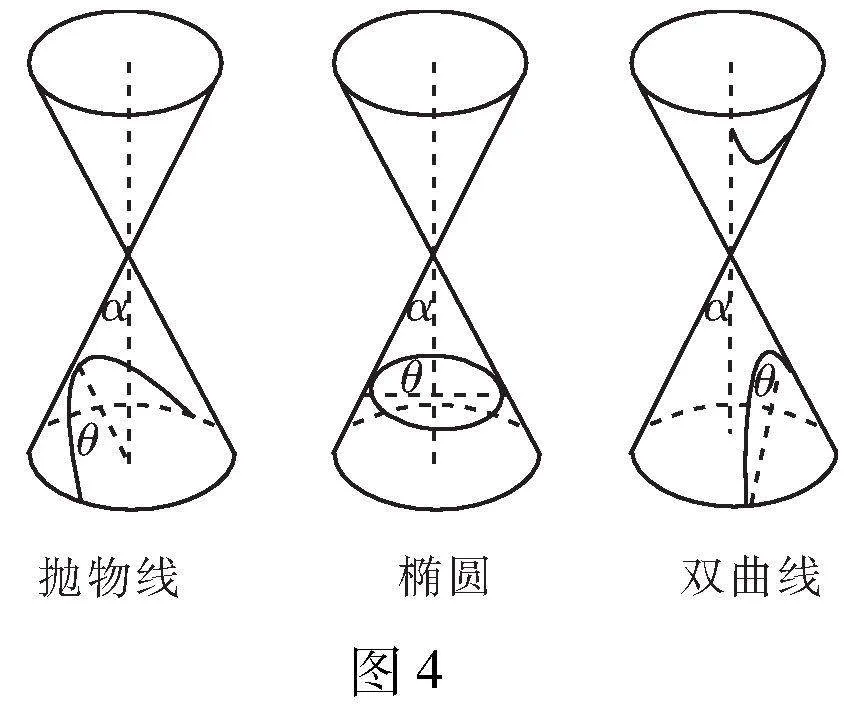
例6 （2023屆衡水中學綜合素養評價10）圓錐曲線為什么冠以圓錐之名？因為它可以從圓錐中截取獲得.我們知道，用一個垂直于圓錐的軸的平面去截圓錐，截口曲線（截面與圓錐側面的交線）是一個圓，用一個不垂直于軸的平面去截圓錐，當截面與圓錐的軸的夾角θ不同時，可以得到不同的截口曲線，它們分別是橢圓、拋物線、雙曲線.因此，我們將圓、橢圓、拋物線、雙曲線統稱為圓錐曲線.截口曲線形狀與θ和圓錐軸截面半頂角α有如下關系（θ，α

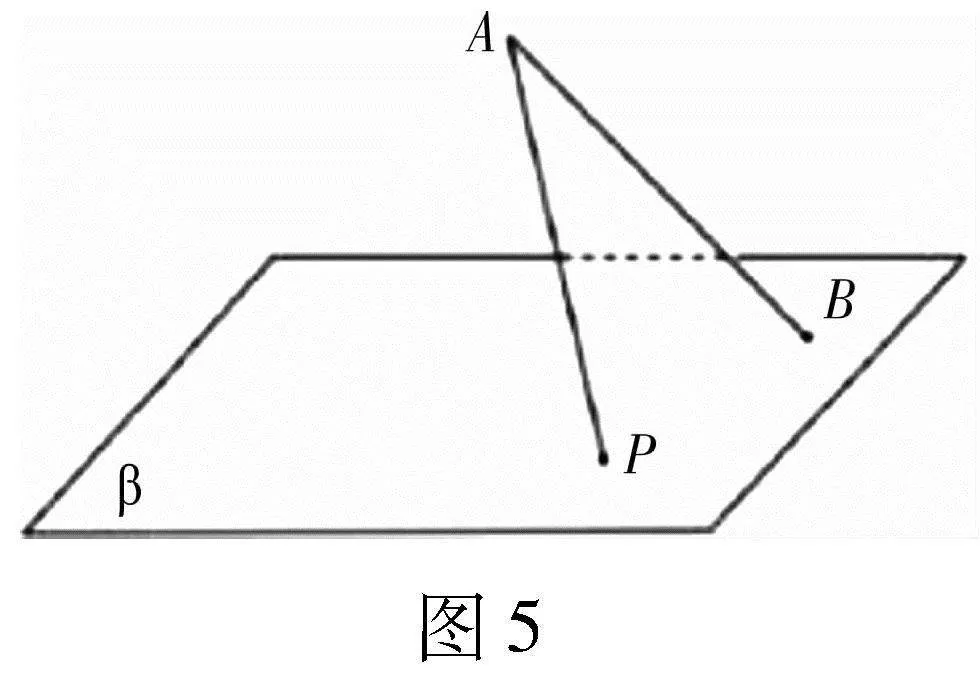
有一定線段AB與平面β夾角φ（如圖5），B為斜足，β上一動點P滿足∠BAP=γ，設P點在β的運動軌圖5跡Г是，則（ ）.

解析：由于AB是定線段，且∠BAP=γ為定值，因此動點P在以AB為軸的圓錐上運動，其中圓錐軸截面的半頂角為γ，β與圓錐軸AB的夾角為φ.對于A，由于φ＞r，所以P點在平面β的運動軌跡Г是橢圓，所以A正確；對于B，由于φ＞r，所以P點在平面β的運動軌跡Г是橢圓，所以B錯誤；對于C，由于φ=r時，所以P點在平面β的運動軌跡Г是拋物線，所以C正確；對于D，由于φ＞r，所以P點在平面β的運動軌跡Г是橢圓，所以D正確.綜上，選ACD.

點評：本題給出圓錐曲線名稱“由來”的背景材料，在對所給材料閱讀理解題的基礎上，設置“軌跡”判斷問題，然后根據題中所給的材料信息，逐一分析作出判斷的.