一道高考函數(shù)試題的題源探究

一般地，解題及命題活動(dòng)過程實(shí)際上是數(shù)學(xué)語(yǔ)言互相轉(zhuǎn)化過程，即圖像語(yǔ)言、符號(hào)語(yǔ)言、自然語(yǔ)言的相互轉(zhuǎn)化過程.命題，常常是把圖像語(yǔ)言轉(zhuǎn)化為符號(hào)語(yǔ)言和自然語(yǔ)言；解題，則是把自然語(yǔ)言轉(zhuǎn)化成圖像語(yǔ)言和符號(hào)語(yǔ)言.命題，是一個(gè)包裝的過程；解題，則是一個(gè)拆包裝的過程.2016年高考全國(guó)I卷的函數(shù)導(dǎo)數(shù)試題，是研究?jī)蓚€(gè)有相同極值點(diǎn)的函數(shù)交點(diǎn)情況，從函數(shù)的圖象特征中提出問題，編制試題．

1.題目呈現(xiàn)

（2016年高考全國(guó)I卷）已知函數(shù)f（x）=x－2ex+ax－12有兩個(gè)零點(diǎn)．

（1）求a的取值范圍；（2）設(shè)x1，x2是f（x）的兩個(gè)零點(diǎn)，證明：x1+x2lt;2．

本題主要考查函數(shù)的零點(diǎn)、導(dǎo)數(shù)及其應(yīng)用、不等式等基礎(chǔ)知識(shí)，考查邏輯推理能力、直觀想象能力、運(yùn)算求解能力和創(chuàng)新能力等，考查函數(shù)與方程思想、化歸與轉(zhuǎn)化思想、分類與整合思想等，考查邏輯推理、直觀想象、數(shù)學(xué)運(yùn)算等核心素養(yǎng)．

2.命題手法

研究一道試題的命題背景和手法，往往是從觀察函數(shù)圖象開始的，這也是數(shù)形結(jié)合思想、直觀想象素養(yǎng)在數(shù)學(xué)學(xué)習(xí)者身上的自然反應(yīng)．我們認(rèn)為本題的命題是從研究?jī)珊瘮?shù)圖象的交點(diǎn)情況開始的．

（1）首先設(shè)定函數(shù)背景．構(gòu)造兩個(gè)有相同極值點(diǎn)1的函數(shù)f1（x）=x－2ex，f2（x）=ax－12，其中兩個(gè)函數(shù)的圖象一動(dòng)一定．

（2）接著觀察圖象變換情況．隨著參數(shù)a的變化，曲線y=f1（x）與y=f2（x）可能有1個(gè)交點(diǎn)，也可能有2個(gè)交點(diǎn)，且兩個(gè)交點(diǎn)到直線x=1的距離不相等．

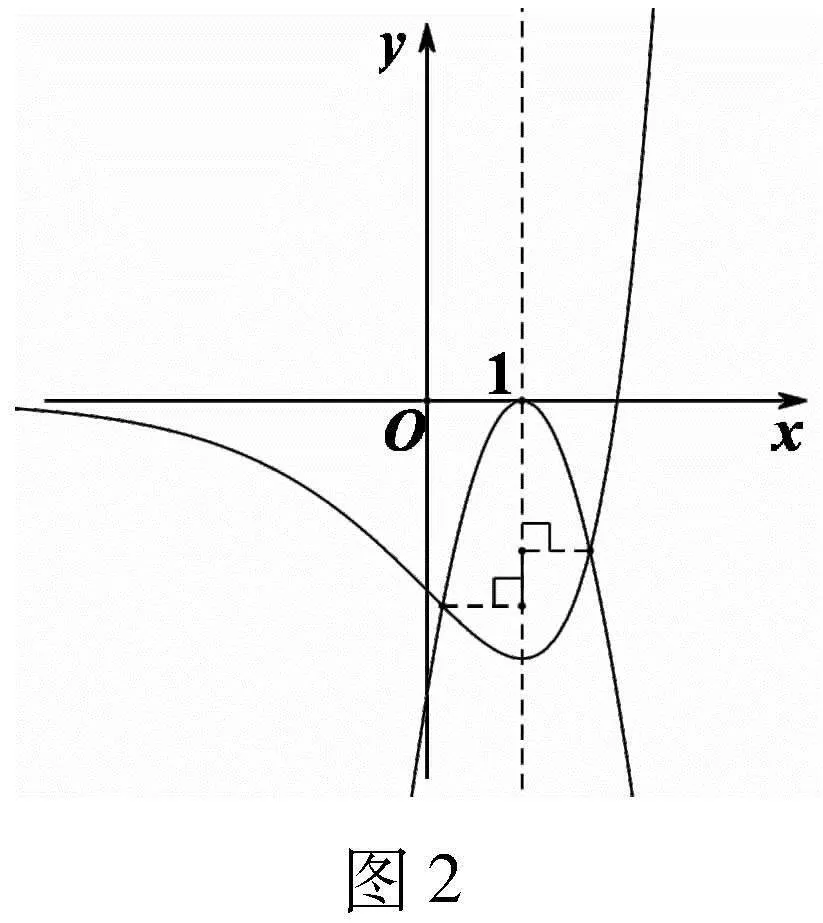
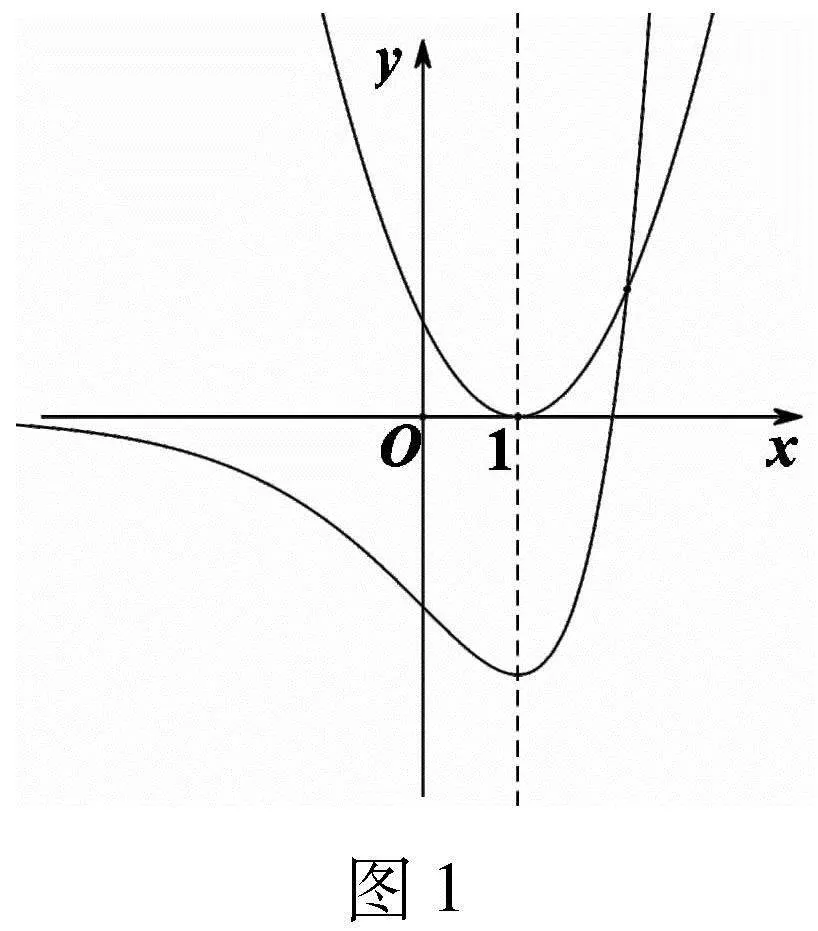
（3）最后根據(jù)觀察的結(jié)果設(shè)置問題．由圖象可以直觀地看到：當(dāng)a=0時(shí)，曲線y=f1（x）與y=f2（x）=0有且只有1個(gè)交點(diǎn)；如圖1，當(dāng)agt;0時(shí)，曲線y=f1（x）與y=f2（x）有且只有1個(gè)交點(diǎn)；當(dāng)alt;0時(shí)，

曲線y=f1（x）與y=f2（x）有且只有2個(gè)交點(diǎn)，如圖2，且左邊交點(diǎn)到直線x=1的距離比右邊交點(diǎn)到直線x=1的距離更遠(yuǎn)．

由此可設(shè)置問題：（i）已知函數(shù)f（x）=x－2ex+ax－12有兩個(gè)零點(diǎn)，求a的取值范圍．

（ii）設(shè)x1，x2是f（x）=x－2ex+ax－12的兩個(gè)零點(diǎn)，證明：x1+x2lt;2．

3.解法探究

解：（1）由已知得f′（x）=x－1ex+2ax－1=x－1ex+2a．

①若a=0時(shí)，由f（x）=0，得x－2ex=0 ，解得x=2，故f（x）只有唯一的零點(diǎn)x=2，不合題意．

③設(shè)alt;0時(shí)，由f′（x）=0得x=1或x=ln－2a．

綜上a的取值范圍為0，+∞．

4.反思拓展

問題（2）可理解為：比較函數(shù)f（x）=x－2ex+ax－12的兩個(gè)零點(diǎn)x1，x2的算術(shù)平均數(shù)與函數(shù)f（x）的極值點(diǎn)1的大小關(guān)系，此類問題我們稱之為“極值點(diǎn)偏移”問題．

關(guān)于兩個(gè)正數(shù)x1，x2的平均數(shù)，《普通高中課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書》介紹了算術(shù)平均數(shù)與幾何平均數(shù)，匡繼昌教授在《常用不等式》中收錄的關(guān)于兩個(gè)正數(shù)的“平均”類型多達(dá)十九種，其中在中學(xué)數(shù)學(xué)常見的有：

并且上述平均數(shù)之間滿足不等關(guān)系H（x1，x2）≤G（x1，x2）≤L（x1，x2）≤E（x1，x2）≤A（x1，x2）≤S（x1，x2） ．

常見的極值點(diǎn)偏移問題，可以比較x1，x2的算術(shù)平均數(shù)，幾何平均數(shù)，調(diào)和平均數(shù)，平方平均數(shù)，對(duì)數(shù)平均數(shù)，指數(shù)平均數(shù)等與極值點(diǎn)的大小． 特別地，命題中的極值點(diǎn)常設(shè)定為常數(shù)1.

參考文獻(xiàn)

［1］ 中華人民共和國(guó)教育部制定．普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版2020年修訂）［M］．北京：人民教育出版社，2020：8．

［2］ 楊蒼洲．幾何直觀素養(yǎng)下的含參數(shù)問題的速解策略［J］．?dāng)?shù)學(xué)通訊，2020（3）：38-39，47．