衛星和飛船的跟蹤測控模型
王 慶,王東強
(蘇州職業大學 基礎部,江蘇 蘇州 215104)
1 問題提出
衛星和飛船在國民經濟和國防建設中有著重要的作用,對它們的發射和運行過程進行測控是航天系統的一個重要組成部分,理想的狀況是對衛星和飛船(特別是載人飛船)進行全程跟蹤測控。
測控設備只能觀測到所在點切平面以上的空域,且在與地平面夾角3度的范圍內測控效果不好,實際上每個測控站的測控范圍只考慮與地平面夾角3度以上的空域。在一個衛星或飛船的發射與運行過程中,往往有多個測控站聯合完成測控任務,如神舟七號飛船發射和運行過程中測控站的分布。
請利用模型分析衛星或飛船的測控情況,具體問題如下:
(1)在所有測控站都與衛星或飛船的運行軌道共面的情況下,至少應該建立多少個測控站才能對其進行全程跟蹤測控?
(2)如果一個衛星或飛船的運行軌道與地球赤道平面有固定的夾角,且在離地面高度為H的球面S上運行。考慮到地球自轉時該衛星或飛船在運行過程中相繼兩圈的經度有一些差異,問至少應該建立多少個測控站才能對該衛星或飛船可能飛行的區域全部覆蓋以達到全程跟蹤測控的目的?
(3)收集我國一個衛星或飛船的運行資料和發射時測控站點的分布信息,分析這些測控站點對該衛星所能測控的范圍。
2 問題分析和模型假設
問題一,假設衛星測控站分布在與衛星軌道共面的地球表面,且衛星的運行軌道為圓。利用幾何關系給出全部覆蓋需要的測控站點數與衛星高度的關系。當衛星的運行軌道為橢圓,衛星運行軌道的一個焦點在地球中心,利用幾何關系給出每個測控站的覆蓋范圍。問題二,在地球自轉的影響下衛星運行過程中星下線的軌跡是地球表面的一些曲線,計算測控站的數量比較困難。一種粗略的估算方法是設置許多測控站,使得其能覆蓋衛星飛過的所有空域。計算這個涵蓋赤道的球面的立體角,再用一個觀測站所能覆蓋的立體角去除得到要覆蓋這個區域至少需要的觀測站。問題三,收集衛星或飛船的發射或運行數據:軌道傾角、高度等;收集該衛星發射和運行過程中觀測站的數據:數量、位置等;給出衛星運行軌道、衛星運行過程中的軌跡方程、每個站的測控范圍、衛星或飛船在運行到某一圈時可測控的范圍,最好能給出一段最長的觀測時間。
3 模型的建立和求解
3.1 問題一
在此問題中(見圖1),我們假設衛星測控站分布在與衛星軌道共面的地球表面。
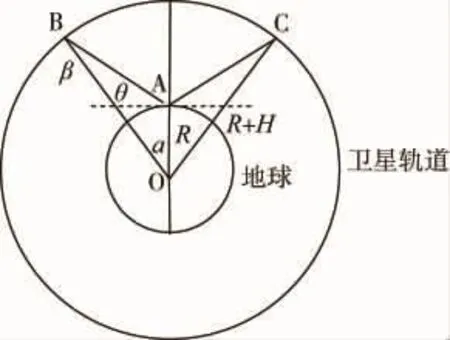
圖1 衛星的運行軌道為圓
首先考慮簡單情形,衛星的運行軌道為圓。
設衛星或飛船飛行對地高度為H,地球半徑為R,衛星的飛行軌道是以地心為圓心R+H為半徑的圓。在A處設有一測控站,測控范圍邊線與地平面的夾角為θ,為確定測控站數應先計算出觀測區域在地球表面上投影所對應的圓心角2α。根據圖1,在ΔABO中,由從而 2α=故所需的測控站個數n(θ,H)為:
由于在實際中衛星或飛船繞地球運轉的軌道是橢圓形的。(見圖2)
我們取橢圓軌道上距地心最近的距離為H0,以地心O為圓心,R+H0為半徑作圓(圖中虛線圓)。由于虛線圓包含在橢圓區域內,若能監控到圓周及其以外空域,則一定能監控到橢圓及以外空域。因此我們只要在地球上均勻建站監控整個虛線圓周。根據上述方法所需的測控站個數為n(θ,H0)。
圖2 衛星或飛船繞地球運轉軌道是橢圓形
3.2 問題二
由于衛星或飛船的運行軌道與地球赤道平面有固定的夾角,而且地球自轉時該衛星或飛船在運行過程中相繼兩圈的經度有一些差異。因此,在地球自轉的影響下衛星或飛船運行過程中星下線的軌跡是地球表面的一些曲線。(見圖3)
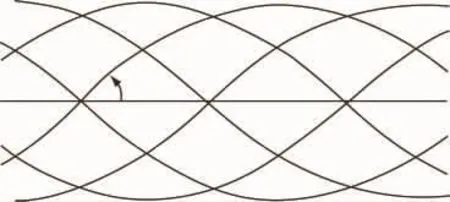
圖3 星下線的軌跡是地球表面的一些曲線
由圖3觀察和分析可以得出:星下點軌跡均勻地分布在赤道的兩邊,即南緯與北緯之間。因此,只需測控南緯與北緯之間的帶狀區域內,就可以實現對該衛星的全程測控。
某一觀測站的觀測區域在以地心為球心,半徑為R+H的球面上,其在地球表面的投影為一球冠(見圖4),面積為S=2πR(R-Rcosα)。衛星或飛船運行軌道在地球表面投影的帶狀區域面積為 S^=4πR2sinλ。若要測控帶形區域內所有的范圍,需測控站的最少個數為帶形區域與球冠面積之比,即

其中,2α表示觀測站在距離為H的高空觀測區域所對應的圓心角,λ為衛星或飛船的運行軌道與地球赤道平面的夾角。神七軌道平面與地球赤道平面的夾角是42.2度,距地面343km,覆蓋這個區域至少需要55個觀測站。
3.3 問題三
根據世界地圖及神舟七號測控通信系統分布圖,我們對其中的測控站進行擬合,發現所成圖形近似正弦函數的曲線。對此,我們試作以下分析,飛船的運行軌道在地球表面上的投影應大致服從正弦曲線分布。測控站的作用是為了能夠更清晰更準確地了解飛船運行的具體情況,故測控站應分布在飛船的運行軌道在地球表面上的投影曲線上。通過查資料獲得神州七號飛船與赤道的夾角為42.2°,高度為343km,周期為90min,小于地球同步軌道運行的高度。由于測控站對飛船的測控范圍彼此會有重復,所以很難計算出測控站點對飛船所能測控的范圍,由于每一個測控站點在地球上的經、緯度已知,所以我們將由地球經緯網展開成的平面圖近似看成是網格圖,從而將空間測控范圍投影在地球經緯網格圖上(見圖4)。我們可以通過計算各測控站點測控范圍的投影圓能覆蓋飛船矩形飛行區域(圖4南北緯42.2°之間)的最小覆蓋數,求得測控站點對神舟七號飛船所能測控的范圍。
我們把飛船矩形飛行區域長k1等分,寬k2等分(不足部分往外延伸),則整個矩形區域被劃分成k1×k2個小正方形區域。經計算

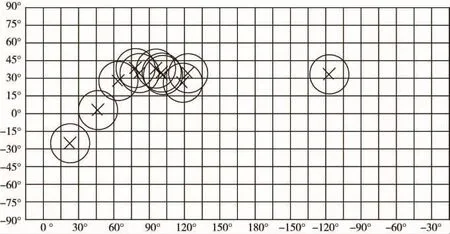
圖4 空間測控范圍投影在地球經緯網格圖
4 結語
對于問題一,我們通過計算觀測區域的張角,得到了衛星或飛船的運行軌道為圓形的情況下,對其進行全程跟蹤測控的測控站數的計算方法。進一步,把圓形軌道推廣到橢圓形軌道。問題二,論證了在地球自轉情況下,衛星在地球表面投影為帶狀區域及觀測區域在地球表面的投影為球冠這一事實,并給出了最少測控站點數的計算方法。在問題3中,通過計算各測控站點測控范圍的投影圓能覆蓋飛船矩形飛行區域的最小覆蓋數,求得測控站點對神舟七號飛船所能測控的范圍。
[1]中國大學生數學建模競賽[EB/OL].www.mcm.edu.cn,2009.
[2]姜啟源,謝金星,葉俊.數學模型[M].3版.北京:高等教育出版社,2003.
[3]柳仲貴.衛星跟蹤系統的動態范圍[J].飛行器測控學報,2003,22(1):3.
[4]韓中庚.數學建模競賽——獲獎論文精選與點評[M].北京:科學出版社,2007.

