一類帶參數的四階Neumann邊值問題解的存在性

黃永峰

(昌吉學院數學系 新疆 昌吉 831100)

一類帶參數的四階Neumann邊值問題解的存在性

黃永峰

(昌吉學院數學系 新疆 昌吉 831100)

通過應用臨界點理論和Morse理論討論了一類帶兩個參數的四階Neumann邊值問題，給出了非平凡解的存在性條件.

Neumann邊值問題;非平凡解;臨界點理論;Morse理論

1 引言

近年來，高階邊值問題由于其在物理及工程學中應用的廣闊性而得到了人們的廣泛關注.許多作者研究了高階邊值問題正解的存在性，得到了一些較好的結果，見文［1，2，3］。他們大都利用錐拉伸或錐壓縮定理以及不動點指數理論在非線性項滿足超線性或次線性條件時獲得結論.也有許多作者利用臨界點理論及Morse理論研究了高階邊值問題解的存在性，見文［4，5，6，7］.特別地，文［5］利用臨界點理論和Morse理論并結合局部環繞定理得到了四階帶參數Dirichlet邊值問題解的存在性.文［7］運用鞍點定理及臨界點理論得到了四階帶參數的Neumann邊值問題的解的存在性.基于以上的研究工作，本文考慮如下的問題

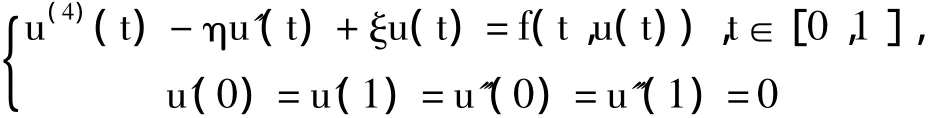
解的存在性，其中f∈C1(［0，1］×R，R)，η，ξ為參數，且滿足條件:

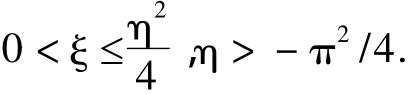
為了證明的需要，本文作如下的幾個條件假設:

2 預備知識

設Gi(t，s)為線性邊值問題，的Green函數.令則有

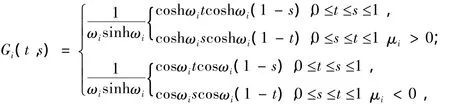
由此知邊值問題在C4［0，1］中的解等價于下列方程

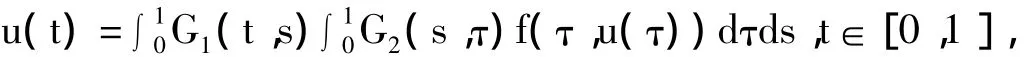
在C［0，1］中的解.

為了結論的證明需要，下面給出一些臨界點理論和Morse理論的基本定義和引理.

定義2.1［8］設D是實Banach空間E中的開集，泛函J:D→R1在D上是Frechet可微，若有u0∈D使得J＇(u0)=0，則稱u0是泛函J的一個臨界點.

定義2.2［8］設E實Banach空間，J∈C1(E，R1).如果{un}?E，J(un)→c，J＇(un)→θ，n→∞蘊涵{un}有收斂子列，則稱泛函J滿足(PS)c條件.如果對于所有的c均滿足(PS)c條件，則稱泛函J滿足PS條件.

定義2.3［9］設J(θ)=0，E=V⊕X，dim V＜+∞，X為實Banach空間.如果存在ρ＞0，使得

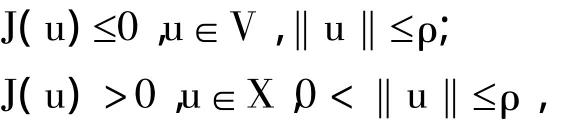
那么稱J在θ點局部環繞.

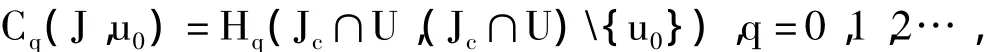
定義2.4［9］設u0是泛函J的一個孤立臨界點，J(u0)=c，U是u0的一個鄰域且在U中J除u0外沒有其它臨界點.我們稱為J在u0的第q個臨界群，其中Hq(X，Y)為第q個奇異相對同調群，其系數為整數群.若至少有一個臨界群是非平凡的，則稱u0是J的一個同調非平凡臨界點.

引理2.1［10］算子方程u=K→fu在C［0，1］中有解當且僅當v=K1/2→fK1/2v在L2［0，1］中有解.引理2.2［4］如果泛函

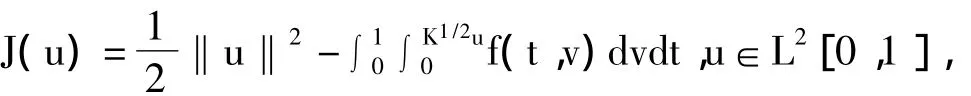
有一個臨界點u∈L2［0，1］，則邊值問題在C4［0，1］中有一個解.

引理2.3［9］假設J∈C1(E，R1)滿足PS條件且在θ點局部環繞，則θ為J的一個同調非平凡臨界點.

定義2.4［9］設p為J的一個孤立臨界點，J∈C2(E，R1).若J＇(p)有有界逆，則稱p為J的一個非退化臨界點.我們稱相應于J＇(p)譜分解的負空間的維數為J在p點的Morse指數，記為ind(J，p).

引理2.4［9］設J∈C2(E，R1)，p為J的一個非退化臨界點，且其Morse指數為j，則Cq(J，p)=δqjZ.

3 主要結論及證明

定理3.1［7］設對k≥1，(H1)和(H2)滿足，那么邊值問題至少有一個解.

引理3.1如果(H3)滿足，那么Cq(J，p)=δqmZ.

此引理在文［5］中已有了詳細的證明，由于在本文中其證明和文［5］中完全類似，故在此省略其證明.

定理3.2假設f(t，0)=0，對k≥1，(H1)和(H2)滿足，且當m≠k時，(H3)成立，那么邊值問題至少有一個非平凡解.

證明設ω為定理3.1所得到的解，我們只需證明ω≠0.因為ω是由鞍點定理在k維子空間的情形下所得到的解，因此我們有Ck(J，ω)≠0.又當條件(H3)滿足時，由引理3.1有Cq(J，p)=δqmZ，注意到m≠k，因此我們有ω≠0.證畢.

引理3.2假設f(t，0)=0，對k＞1，(H1)和(H4)滿足，那么泛函J具有山路型結構，亦即J(θ)=0且滿足

(i)存在β，ρ＞0，使得J(u)≥β，u∈L2［0，1］，‖u‖=ρ;

(ii)存在e∈L2［0，1］，使得‖e‖＞ρ且J(e)＜0.

證明由(H4)知，存在δ＞0，α＞0，使得.選取ρ=α/L1，其中L1為 K1/2:L2［0，1］→C［0，1］的范數，當‖u‖＜ρ時，我們有‖K1/2u‖C≤L1·‖u‖≤α，則有

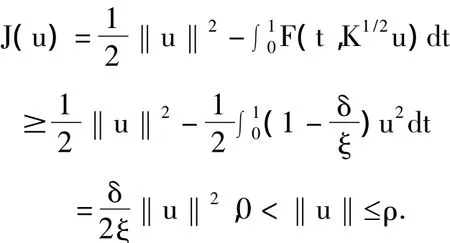
由此知(i)滿足.

取e0為特征值λ0=1/ξ對應的標準向量我們知

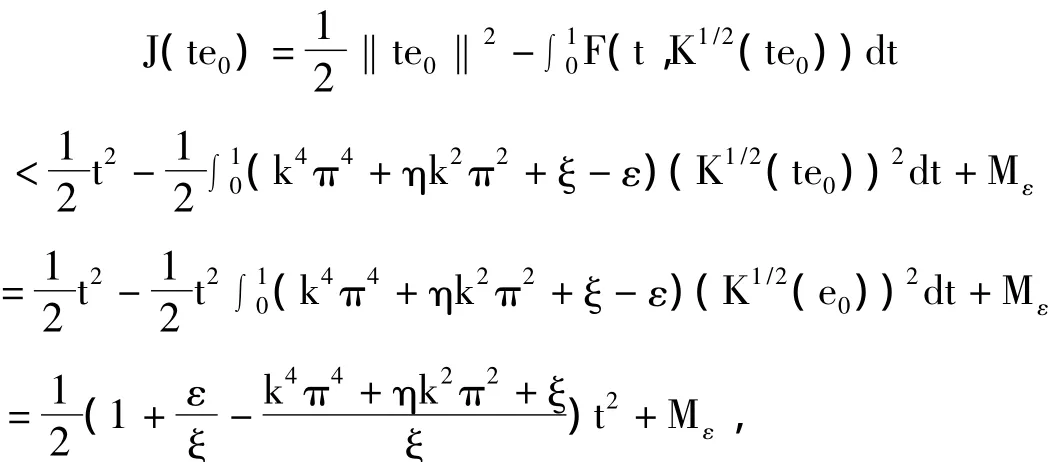
其中Mε為某個正數，上式不等號處用到了條件(H1).注意到k≥1，選取充分小的ε，使得

，因此有J(te0)→－∞，t→+∞，故對充分大的t0＞ρ，有J(te0)≤0.由此知(ii)滿足.證畢.

定理3.3假設f(t，0)=0，對k＞1，(H1)，(H2)和(H4)滿足，那么邊值問題至少有兩個平凡解.

證明由引理3.1和引理3.2，通過運用山路引理，我們得到邊值問題的一個非平凡解.因為為山路型的解，由文［11］中推論8.5知.因為k＞1，易知.設ω為定理3.1所給出的解，我們有Ck(J，ω)≠0，所以ω≠ω－.由引理3.2的(i)的證明我們知θ是J的一個孤立局部極小值，故有Cq(J，θ)=δq0Z，故ω≠θ.證畢.

［1］Z.Bai，H.Wang.On positive solutions of some nonlinear fourth－order beam equations［J］.J.Math.Anal.Appl.2002，270:357－368.

［2］B.Liu.Positive solutions of fourth－oder boundary value problems［J］.Appl.Math.Comput.，2004，148:407－420.

［3］C.Pang，W.Dong，Z.Wei.Multiple solutions for fourth－order boundary value problem［J］.J.Math.Anal.Appl.2006，314:464－476.

［4］X.Liu，W.Li.Existence andmultiplicity of solutions for fourth order boundary value problemswith parameters［J］.J.Math.Anal.Appl.2007，327，362－375.

［5］Y.Yang，J.Zhang.Existence of solutions for some fourth－order boundary value problemswith parameters［J］.Nonlinear Anal.2008，69:1364－1375.

［6］G.Han，Z.Xu.Multiple solutions of some nonlinear fourth－order beam equations［J］.Nonlinear Anal.，2008，68: 3646－3656.

［7］黃永峰.一類帶參數的四階Neumann邊值問題解的存在性［J］.昌吉學院學報，2011，(1):104－108.

［8］郭大鈞.非線性泛函分析(第二版)［M］.濟南:山東科學技術出版社，2001.

［9］K.Chang.Infinite Dimensional Morse Theory and Multiple Solution Problems［M］.Birkhauser，Boston，1993.

［10］F.Li，Z.Liang，Q.Zhang.Existence of solutions of a class ofnonliear second order two－pointboundary value problems［J］.J.Math.Anal.Appl.，2005，312:357－373.

［11］J.Mawhin，M.Willem.Critical Point Theory and Hamiltonian Systems［M］.Springer Verlag，New York，1989.

2011－05－20

昌吉學院科研基金項目(2010SSQD024)

黃永峰(1985－)，男，湖北天門人，昌吉學院數學系，助教，研究方向:非線性泛函分析。

O175.8

A

1671－6469(2011)04－0097－04

(責任編輯:代琴)