可變精度粗糙集在上市公司財務預警中的運用

　　【摘要】 可變精度粗糙集VPRS是標準粗糙集RS的一種推廣。文章借鑒了VPRS模型具有噪聲數據的強適應能力和強抗干擾能力的優點，提出了一類基于VPRS的信息產業上市公司財務預警方法，并用部分信息產業上市公司對其進行實證檢驗。檢驗結果表明：該方法具有較好的識別能力，對信息產業上市公司財務危機的預測準確率達到89.7%，具有良好的應用前景。
　　【關鍵詞】 信息產業； 財務預警； 可變精度粗糙集； R約簡； 決策樹
　　
　　一、引言
　　
　　改革開放以來，我國信息產業發展迅速，已逐步成為國民經濟重要的支柱性、先導性、基礎性和戰略性產業。信息產業類企業，包括致力于信息技術研發和服務的企業，具有較強的擴張性、滲透性，資金需求量大，但由于受到信息技術生命周期、研發成熟度、市場容量、經營能力等因素的影響，其未來發展和經營業績具有較大的不確定性，導致企業面臨較大的經營風險和財務風險。其中，信息產業上市公司的財務信息對多方利益相關者都有著重要影響。因此，建立財務預警系統、強化財務管理、避免財務失敗和破產，具有重要意義。
　　現有的企業財務預警方法可分為定性預警與定量預警兩類。定性分析主要包括：災害理論、專家調查法、四階段癥狀等方法。定量分析主要包括：單變量判定模型、多變量線性判定模型、Logistic回歸模型、人工神經網絡模型等方法。上述方法各有其特點，但均存在不同程度的局限，難以滿足企業財務預警實踐發展的需要。粗糙集（RS）是一種刻畫不完整性和不確定性的數學工具，能有效分析不精確、不一致、不完整等各種不完備信息，還可以對數據進行分析和推理，從中發現隱含的知識，揭示潛在的規律，從而有效進行知識庫的約簡和規則的提取。
　　可變精度粗糙集（VPRS）是對RS理論的擴充，它在標準粗糙集的基礎上引進一個閾值β，并將其定義為錯誤分類率（0≤β＜0.5），即允許一定程度上錯誤分類率的存在，由此，使VPRS具有較強的抗干擾能力。An等（1996）又將β定義為正確分類率（0.5≤β＜1），并稱之為強化粗糙集。文獻［6］運用VPRS模型對我國166家上市公司財務困境進行預測，取得了較高的預測精度。文獻［7］顯示VPRS模型在應用過程中面臨參數β的選擇問題，不同的β值將產生不同的屬性約簡結果。有鑒于此，本文將VPRS引入到信息產業上市公司財務預警分析中，提出一種基于VPRS的信息產業上市公司財務預警方法。首先，根據VPRS模型對屬性進行R約簡并生成識別規則，形成識別規則庫；然后，在識別規則庫的基礎上集成剪枝決策樹，構建信息產業上市公司財務危機識別方法；最后，利用測試樣本對識別方法進行檢驗并獲取識別精度。結果顯示，該方法對信息產業上市公司財務危機的預測準確率達到89.7%，具有良好的應用前景。
　　
　　二、基于VPRS的信息產業上市公司財務預警方法
　　
　　步驟1：建立決策數據表，對原始數據進行補缺。使用決策表來描述對象，即采用二維數據關系表的形式。表中每一行描述一個對象（即樣本企業），每一列描述對象的一種屬性。在實際收集數據的過程中，不可避免地會遇到數據缺失情況。為此，擬采用Mean/mode方法對數據進行補缺。
　　步驟2：對樣本數據進行劃分及離散化處理。按2∶1的比例將完備數據關系表劃分為兩個數據關系表，其中，總樣本的67%為訓練樣本，用來導出識別規則，形成識別規則庫；剩余的33%為測試樣本，用來檢驗識別方法，獲取識別精度。運用VPRS模型處理數據關系表時，要求表中的屬性值用離散數據表示，而大部分樣本企業的條件屬性均為連續值，因此，必須對樣本數據進行離散化處理。擬采用等頻率劃分方法對數據進行離散化處理。
　　步驟3：R約簡與規則生成。VPRS模型常用的屬性約簡算法有：R約簡、上下分布約簡等。其中，R約簡是通過全局增益來度量決策信息系統的屬性重要程度，并以全局增益作為啟發式信息得出VPRS屬性約簡的啟發式算法。本文擬采用R約簡，通過啟發式算法對訓練樣本進行屬性約簡。根據約簡結果，生成具有一定決策概率的不精確決策規則。通過設定相關的可信度、覆蓋率、支持數閾值，對生成的規則進行篩選，形成識別規則庫。
　　步驟4：集成剪枝決策樹，構建信息產業上市公司財務危機識別方法，并對其進行檢驗。首先，在識別規則庫的基礎上，運用基于VPRS的決策樹生成方法，建立基于識別規則的決策樹。即通過計算各規則的變精度明確區，選取明確區最大的規則作為第1條規則，用第1條規則對待識別樣本進行識別；其次用第2條規則對第1條規則不能識別的剩余樣本進行識別，以此類推；再次，運用基于RS的決策樹剪枝算法得到剪枝決策樹，從而構建起信息產業上市公司財務危機識別方法；最后，利用測試樣本對識別方法進行檢驗，獲取識別精度。
　　
　　三、實證分析
　　（一）指標體系和樣本數據
　　
　　本文參考國內外有關文獻提出的企業財務預警指標體系，遵循指標選取的系統性、科學性及可操作性等原則，從償債能力、營運能力、盈利能力等五個方面，選取流動比率、速動比率、資產負債率、利潤總額、財務費用、已獲利息倍數、存貨周轉率、應收賬款周轉率、凈資產收益率等21項財務指標建立信息產業上市公司財務預警指標體系。
　　選取滬、深股市中有代表性的信息產業上市公司作為實驗樣本，數據來源于證券之星網站。將上市公司因財務狀況出現異常而被特別處理（ST）作為財務危機的標志。對于ST公司，采用被ST的前兩年數據來進行預測分析，以判斷其最終是否會陷入財務危機，樣本區間設定為2004—2008年。對于非ST公司，則采用2008年的年報數據。在剔除異常數據樣本，并對原始數據進行補缺后，最終獲得88家樣本公司，其中，定義0為財務危機公司，即ST公司，共28家；定義1為財務健康公司，即非ST公司，共60家。隨機抽取19家ST公司和40家非ST公司作為訓練樣本，剩余的29家公司作為測試樣本。
　　（二）R約簡與規則生成
　　采用等頻率劃分方法對原始數據進行離散化處理。運用啟發式算法對屬性進行R約簡，59個訓練樣本共產生了36條約簡。在這些約簡中，存在部分冗余無效的約簡，為了提高約簡的有效性，選取強度大于80的約簡，共計12個。從屬性約簡結果可以看出：流動比率、速動比率、資產負債率、財務費用、已獲利息倍數、存貨周轉率、應收賬款周轉率、凈資產收益率、利潤總額等9個指標對信息產業上市公司的財務預警具有重要影響。
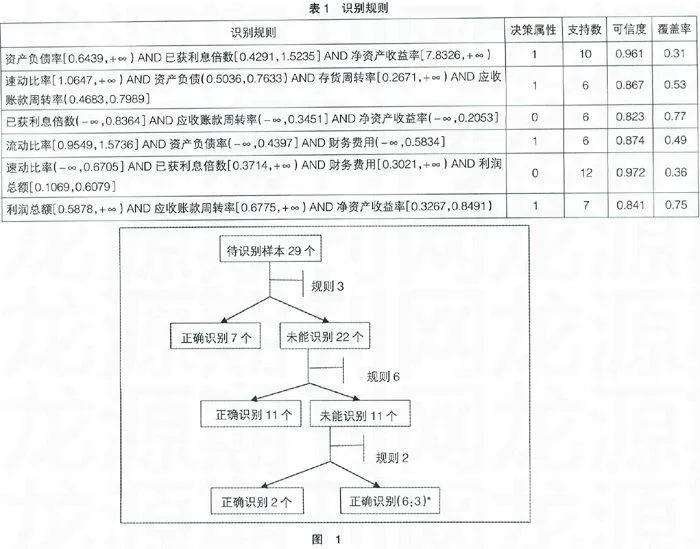
　　在上述約簡的基礎上，利用Rosetta軟件生成規則，設定限制條件為可信度>70%、覆蓋率>5%，最終得到36條識別規則。限于篇幅，表1顯示了其中可信度>80%的6條識別規則。表1中每一行表示一條識別規則。例如，第一行表示：當識別指標中資產負債率在0.6439以上，已獲利息倍數在0.4291至1.5235之間，凈資產收益率在7.8326以上時，樣本公司的財務狀況較好。該識別規則的支持數為10，可信度為0.961，覆蓋率為0.31。
　　（三）財務危機識別方法的構建與檢驗
　　決策樹又稱判定樹，是一種類似于二叉或多叉的樹結構，與其它分類模型相比，決策樹簡潔易懂，容易轉換成規則，且具有與其它分類模型相同的，甚至是更好的分類準確性。
　　VPRS在建立近似區間時，允許等價類以小于某個錯誤分配率（通常設β=0.2）的概率劃入近似區間。由此，引入變精度明確區與非明確區的定義，將誤差限內的實例劃入VPRS的下近似中，成為能明確分類的實例，從而提高了分類的正確性和對未來數據的泛化能力。有鑒于此，本文運用基于VPRS的決策樹生成方法，構建基于識別規則的決策樹。決策樹由根節點、分支和葉節點組成，這里的根節點是待識別樣本，分支是待識別樣本能否被識別規則正確識別，葉節點被分為正確識別樣本和未能識別樣本兩類。為了在保證一定正確率的前提下得到盡可能簡單的決策樹，本文還運用基于RS的決策樹剪枝算法對規則進行修剪。根據RS理論中近似空間的定義，首先給出明確度的概念來衡量數據被明確分類的程度，采用深度擬合率和錯誤率作為剪枝標準，同時考慮了樹的復雜度和樹的分類精度。剪枝過程自下而上持續進行，直至不能再剪枝為止。
　　
　　利用29個測試樣本對信息產業上市公司財務危機識別方法進行檢驗。每條規則可以將待識別樣本分為正確識別和未能識別兩類，設定誤差參數β=0.2，對每個規則，計算其變精度明確區的大小，得出規則3的變精度明確區最大，說明規則3相對其它規則而言，能夠提供更多的分類信息。選取規則3作為第1條規則，從根節點出發對29個測試樣本進行判定，依次類推。運用基于RS的決策樹剪枝算法，取閾值0.1及0.05，從決策樹的最低層開始進行剪枝，得到剪枝決策樹，如圖1所示。圖1括號中以*標識的數字X∶Y為到達此葉節點的多數例與反數例，X代表多數實例數，Y代表反例數，即有6個樣本被正確識別，3個樣本不能識別。圖1顯示：從29個測試樣本中可以準確識別出26個樣本的財務狀況，只有3個樣本不能識別，預測準確率達到89.7%。
　　
　　四、結論
　　
　　將VPRS引入到信息產業上市公司財務預警分析中，提出一種基于VPRS的信息產業上市公司財務預警方法。在對樣本數據進行預處理后，首先，根據VPRS模型，對屬性進行R約簡并生成識別規則，形/48I/c90y5A5R7J3UodWjQ==成識別規則庫；然后，在識別規則庫的基礎上，集成剪枝決策樹，構建信息產業上市公司財務危機識別方法；最后，利用測試樣本對識別方法進行檢驗，獲取識別精度。實證結果表明，本文提出的財務預警方法對信息產業上市公司財務危機的預測準確率達到89.7%，具有良好的應用前景。本文的研究為提高企業財務危機預測精度提供了新的方法和思路。但VPRS在引入誤差參數的同時，也不排除向近似區間引入誤差或噪聲的可能性，如何合理選擇誤差參數β有待于進一步研究。
　　
　　【參考文獻】
　　［1］ 李志強.上市公司財務預警研究述評［J］.金融理論與實踐，2009（3）：86-90.
　　［2］ Pawlak Z.Rough Sets［J］.Int.J.Coumput.Inf.Sci，1982（11）：341-356.
　　［3］王國胤.Rough集理論與知識獲取［M］.西安：西安交通大學出版社，2001：99-142.
　　［4］ Ziarko W.Variable Precicsion Rough
　　Set Model［J］.Journal of Computer and System Sciences，1993，46（1）：39-59.
　　［5］ An A，Shan N，Chan C，et al.Discovering rules for water damand prediction：An enhanced rough-set approach［J］.Engineering Application and Artifical Intelligence，1996，9（6）：645-653.
　　［6］ 胡援成，程建偉.基于可變精度粗糙集模型的上市公司財務困境預測［J］.當代財經，2007（5）：32-36.
　　［7］ 庾慧英，劉文奇. 變精度粗糙集模型中取值范圍的確定［J］.昆明理工大學學報，2005（12）：109-111.
　　［8］ 王加陽，陳松喬，等.可變精度粗糙集模型研究［J］.計算機與數字工程，2005（8）：53-54
　　［9］ 顧靖，周宗放.基于可變精度粗糙集的新興技術企業信用風險識別［J］.管理工程學報，2010（1）：70-76.
　　［10］ Vapnik V. Statistical Learning Theory［M］.New York：John Wiley，1998：1-173.
　　［11］ 桑妍麗.變精度粗糙集下基于信息熵的屬性約簡算法［J］.山西師范大學學報，2005（3）：27-30.
　　［12］ 王名揚.基于粗糙集理論的決策樹生成與剪枝方法［D］.東北師范大學碩士學位論文，2005：47-52.