卡爾多爐處理銅陽極泥生產(chǎn)多爾合金配料工藝優(yōu)化實(shí)踐
陳占飛
(紫金銅業(yè)有限公司,福建 上杭 364200)
卡爾多爐又稱斜吹轉(zhuǎn)爐,用于處理銅陽極泥始于1993年。自2007年至今,國(guó)內(nèi)已陸續(xù)有數(shù)家企業(yè)采用該工藝從銅陽極泥中回收金、銀、硒、碲等。某企業(yè)采用0.8m3卡爾多爐,設(shè)計(jì)年處理銅陽極泥2000t,已正式投產(chǎn)。
1 前期生產(chǎn)中的主要問題
單爐作業(yè)周期長(zhǎng),能耗高,銀直收率低。通過先排上層稀渣,再加少量焦粉繼續(xù)熔煉、排渣的方法,渣中銀含量并降低不明顯,反而使焦粉消耗增加、熔煉周期更加延長(zhǎng);另外,高溫熔體中直接加入焦粉時(shí),爐內(nèi)反應(yīng)劇烈,易導(dǎo)致噴爐。其次,吹煉渣粘稠、渣量大,噴槍及喇叭口粘渣嚴(yán)重,吹煉溫度難以控制,喇叭口須每爐清理一次,勞動(dòng)強(qiáng)度大。
2 主要問題分析與優(yōu)化
2.1 還原劑配比對(duì)主要作業(yè)指標(biāo)影響分析
元素氧位與溫度關(guān)系圖[1]分析可知,一定范圍內(nèi),還原劑配比增加,金、銀、鉛及其他雜質(zhì)還原會(huì)更加充分,有利于提高金、銀直收率。但熔煉終點(diǎn)將持續(xù)后延,熔煉周期延長(zhǎng),能耗增加,卡爾多爐作業(yè)效率下降。圖1為實(shí)際條件下,焦粉配比與渣含銀及熔煉周期關(guān)系。
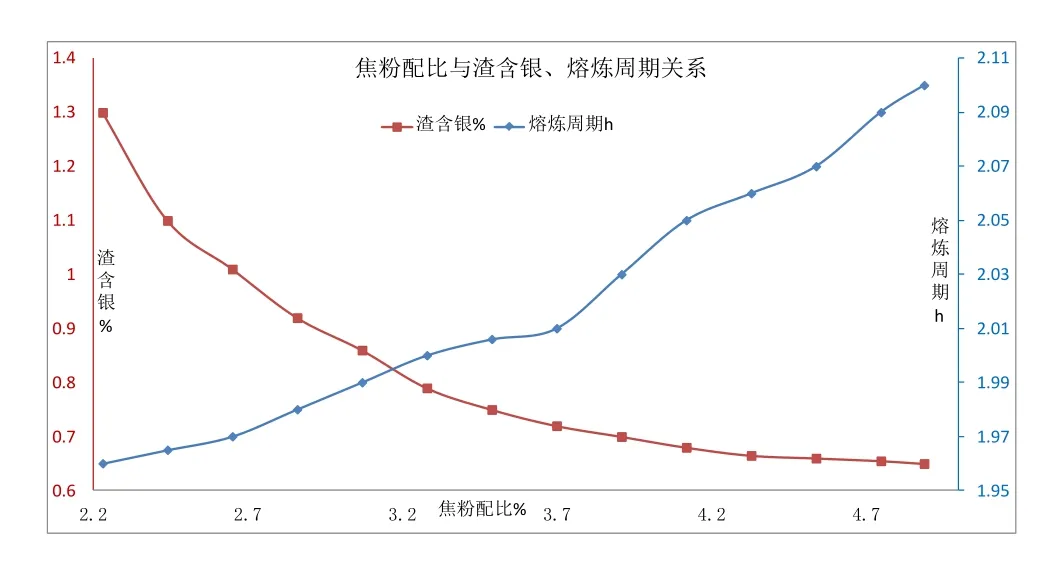
圖1 焦粉配比與渣含銀及熔煉周期關(guān)系
隨著還原劑配比上升,貴鉛中Pb及其他雜質(zhì)含量增加,將導(dǎo)致后續(xù)吹煉周期延長(zhǎng),除鉛所用石英砂量也會(huì)逐漸增加,吹煉渣中銀損失高,各種能耗上升,作業(yè)效率下降。圖2為實(shí)際條件下,焦粉用量與吹煉周期及除鉛用石英砂耗量關(guān)系。
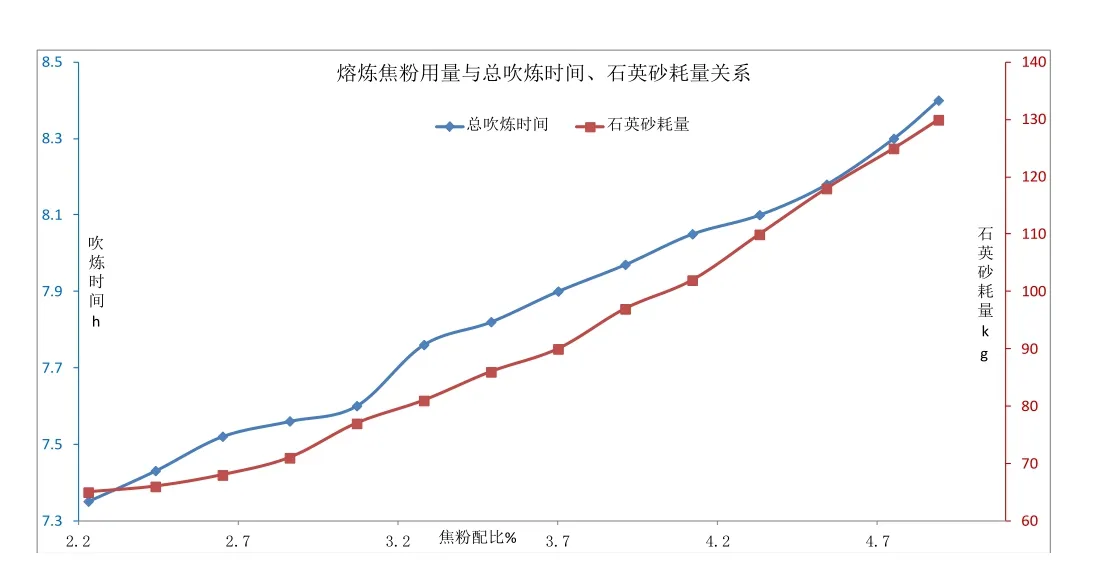
圖2 焦粉用量與吹煉周期及除鉛用石英砂耗量關(guān)系
由圖1、圖2可知,焦粉配比增加僅利于提高銀直收率,而且隨著焦粉配比提高至4.0%,熔煉渣中銀含量降低幅度不再明顯。對(duì)焦粉配比在2.6%以上的熔煉渣進(jìn)行物相分析,結(jié)果顯示渣中銀為游離態(tài),且此時(shí)貴鉛中Pb已高達(dá)40%以上,表明實(shí)際焦粉配比偏高。
2.2 指標(biāo)調(diào)整優(yōu)化
擬通過進(jìn)一步降低熔煉渣粘度,提高貴鉛與渣的分離效果,以達(dá)到提高銀直收率的目的。根據(jù)硅酸鹽熔體聚合物理論[2],適當(dāng)提高蘇打加入量可以降低爐渣粘度。且由反應(yīng)(1)、反應(yīng)(2)可知,Na2CO3可代替焦粉與陽極泥中Ag2SO4反應(yīng)生成單質(zhì)Ag,有利于進(jìn)一步降低熔煉焦粉消耗。

逐漸下調(diào)焦粉配料比、上調(diào)蘇打加入量,經(jīng)過對(duì)比調(diào)整,貴鉛中Pb由40%以上降至18%~20%,銀直收率、石英砂及氧化鉛消耗等指標(biāo)均得到好轉(zhuǎn);達(dá)到熔煉終點(diǎn)后一次性排出熔煉渣,不必額外加入焦粉繼續(xù)熔煉,操作簡(jiǎn)化,熔煉時(shí)間更短。陽極泥、吹煉渣熔煉指標(biāo)對(duì)比如表1、表2,吹煉石英砂耗量及單爐周期指標(biāo)對(duì)比如表3。
實(shí)際統(tǒng)計(jì)平均每爐次主要消耗指標(biāo):除蘇打耗量增加212.3kg外,氧化鉛、石英砂、焦粉耗量分別下降117.8kg、85.1kg、185.6kg,折合成本下降約3073元/爐次,節(jié)約輔料成本約80萬元/年;Ag直收率上升1.953%,卡爾多爐作業(yè)效率提升8.91%。此外,喇叭口粘結(jié)情況也得到明顯改善,減少為每?jī)蔂t清理一次,平均每爐系統(tǒng)清理時(shí)間減少1.85h。

表1 陽極泥熔煉指標(biāo)對(duì)比
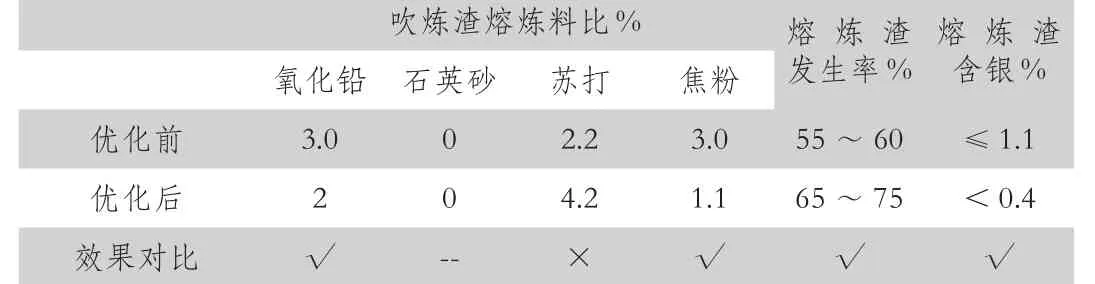
表2 吹煉渣熔煉指標(biāo)對(duì)比

表3 吹煉石英砂耗量及單爐周期指標(biāo)對(duì)比
2.3 相關(guān)問題及措施
問題:配料優(yōu)化后,蘇打配入量上升且粒度過細(xì),導(dǎo)致爐料透氣性變差,蘇打高溫分解為CO2生成量增加,使?fàn)t況變差,易導(dǎo)致噴爐發(fā)生。
措施:調(diào)整爐料配料順序,將蘇打置于每小批爐料最下層優(yōu)先加入爐內(nèi),以增強(qiáng)上層爐料透氣性。蘇打與爐內(nèi)高溫熔體直接接觸,使蘇打附近溫度能夠盡快達(dá)到近1200℃[3]而分解,及時(shí)生成CO2并逸出,從而降低了爐內(nèi)蘇打聚集量,為后續(xù)批次蘇打的配入提供安全條件,有效地解決了上述問題。
3 結(jié)語
通過進(jìn)一步降低爐渣粘度有效解決了銀直收率低的問題;通過降低焦粉消耗明顯縮短了單爐作業(yè)周期,提高了卡爾多爐作業(yè)效率,產(chǎn)量得到提升,規(guī)模效益凸顯。考慮到原料成分波動(dòng)情況,生產(chǎn)中將貴鉛中Pb18%~20%作為還原劑調(diào)整的參考依據(jù)。熔煉渣Pb/SiO2控制在3.0為宜。

