圓錐曲線動弦的“保值性”

☉江蘇省灌云縣楊集高級中學(xué) 李 昌

圓錐曲線的許多性質(zhì)不僅優(yōu)美而且和諧.文［1］得到了圓錐曲線中關(guān)于動弦的性質(zhì)1.

性質(zhì)1過圓錐曲線上一定點P任作兩條動弦PA、PB，當(dāng)這兩弦的斜率之積、斜率之和或者傾斜角之和三者中有一個為定值時，動弦AB所在直線過定點或有定向.

此性質(zhì)動靜結(jié)合，很優(yōu)美，但不具和諧性！因為條件中的動弦有兩條，且它們在方向上存在某種靜態(tài)，而結(jié)論中的動弦只有一條，其靜態(tài)也不完全體現(xiàn)在方向上.由此想到：是否可以找到兩條直線，它們的方向存在與條件相對應(yīng)的靜態(tài)呢？

結(jié)合性質(zhì)1，進(jìn)一步探究發(fā)現(xiàn)，動弦AB過定點Q時，直線PQ和曲線在點P處的切線l與動弦PA、PB在方向上具有一致的定值；動弦AB有定向時，動弦AB和曲線在點P處的切線l與動弦PA、PB在方向上也具有一致的定值.據(jù)此，既能使條件的定值在結(jié)論中得到保全，又能使定點定向歸為統(tǒng)一，結(jié)論更優(yōu)美和諧.故將其稱為圓錐曲線動弦的“保值性”，即：

性質(zhì)2過圓錐曲線上一定點P任作兩條動弦PA、PB，設(shè)圓錐曲線C在點P處的切線為l，用kPA表示直線PA的斜率，αPA表示直線PA的傾斜角，其他類似.

（1）當(dāng)kPA·kPB=t（t為定值）時，動弦AB所在直線若過定Q，在kPQ存在時，滿足kPQ·kl=t，動弦AB若有定向，在kAB存在時，滿足kAB·kl=t；

（2）當(dāng)kPA+kPB=t（t為定值）時，動弦AB所在直線若過定Q，在kPQ存在時，滿足kPQ+kl=t，動弦AB若有定向，在kAB存在時，滿足kAB+kl=t；

（3）當(dāng)αPA+αPB=α（α為定值）時，動弦AB所在直線若過定Q，則αPQ+αl=α，若有定向，則αAB+αl=α.

下面利用文［1］的結(jié)論以拋物線和橢圓為例進(jìn)行證明，雙曲線中的證明類似.

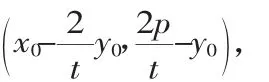
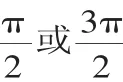
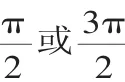
1.朱其錄，申后坤.圓錐曲線動弦的一個性質(zhì).數(shù)學(xué)通報，2002，11.