中學數學中的幾個漸近線問題及處理對策
☉江蘇省昆山中學 戈 峰
中學教材中出現“漸近線”這個概念是在“雙曲線的簡單性質”這節中,概括為:曲線上的動點沿著曲線從某個方向向外延伸時,動點與某條直線無限地接近,但永遠不相交,那么稱此直線為曲線的漸近線(滲透極限思想).中學數學的許多函數圖像和曲線都有漸近線,例如教材中涉及到的初等函數:反比例函數、指對數函數、正余切函數等.學生在學習過程中若能領會漸近線的內涵,就能對掌握某些函數的形狀、位置、大小等有很大的幫助.本文對中學數學中有漸近線的一些復雜函數進行討論,并對處理有漸近線的函數問題提供幾種策略.
一、分類討論
除了教材中我們比較熟悉的反比例函數、指對數函數、正余切函數圖像有漸近線外,我們經常碰到圖像有漸近線的函數主要有分式函數型與超越函數型.
1.分式函數型.
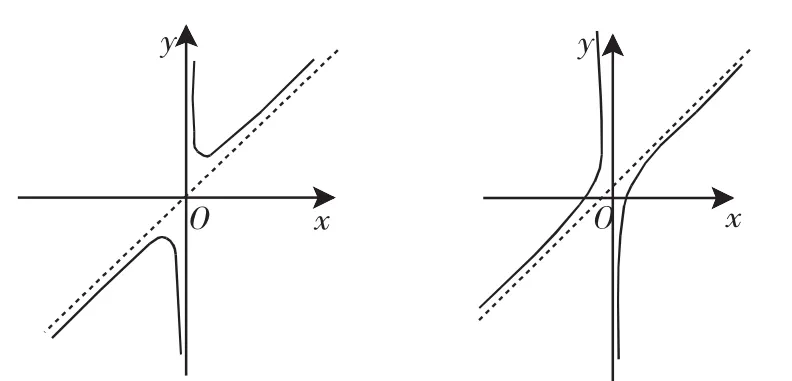
圖1圖2

以a>0,d>0,h>0進行分析:
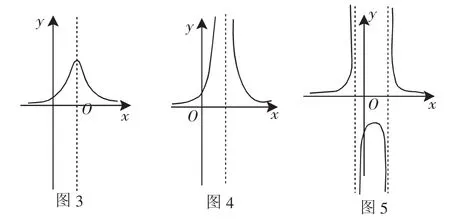
對于①,f(x)關于x=k對稱,當x趨向于無窮時,a(x-k)2+h趨向于正無窮,則f(x)趨向于0,所以x軸是f(x)的漸近線.如圖3.
對于②,f(x)關于x=k對稱,當x趨向于無窮時,a(x-k)2趨向于正無窮,則f(x)趨向于0,當x趨向于k時,a(x-k)2趨向于0,則f(x)趨向于正無窮,所以x軸與x=k是f(x)的漸近線.如圖4.
對于③,當x趨向于無窮時,a(x-m)(x-n)趨向于正無窮,則f(x)趨向于0.當x趨向于m和n時,a(x-m)(x-n)趨向于0,則f(x)趨向于正無窮,所以x軸、x=m與x=n都是f(x)的漸近線.如圖5.

2.超越函數型.
(1)函數f(x)=xn·ex(n∈Z).
當n=0時,f(x)=ex以x軸為漸近線;
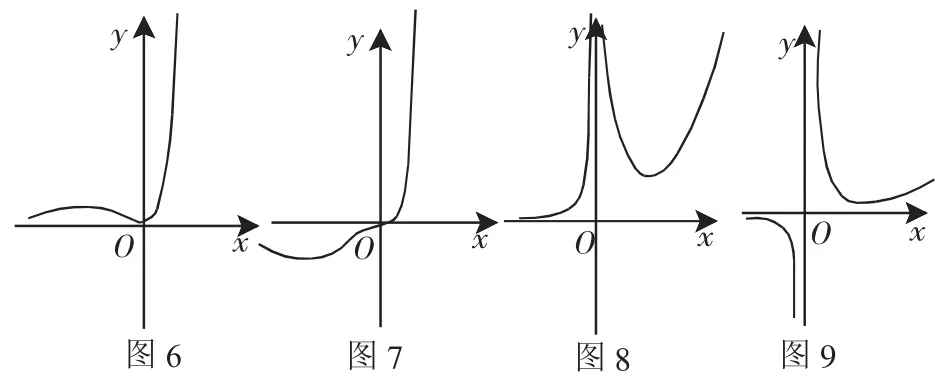
當n>0時,f′(x)=xn-1·ex(n+x),易得f(x)在x=0處取得極小值,在x=-n處取得極大值;n為偶數時,f(x)在x=0處為拐點,在x=-n處取得極小值.而當x趨向于正無窮時,f(x)都趨向于正無窮.x趨向于負無窮時,f(x)趨向于0.所以f(x)=xn·ex以x軸為漸近線,如圖6(n=2)和圖7(n=3).

二、應對策略
1.思想重視.
在學習函數性質時除了要重視函數的定義域、值域、單調性、奇偶性、對稱性、特殊點等性質外,也要重視函數圖像是否具有漸近線這一性質.
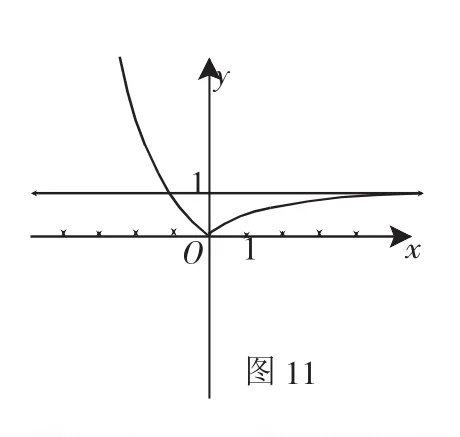
解析:畫出圖像如圖11,圖像的漸近線為y=1,要求y=m與y=有兩個交點,所以m∈(0,1).
2.取倒數.
解析1:方程的一個解為x=0.
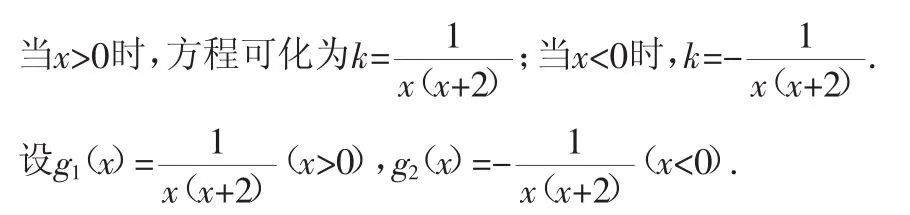
由分式函數型(2)討論可知,x軸,y軸是g1(x)的漸近線;x=-2,x軸,y軸是g2(x)的漸近線.
因此g1(x)和g2(x)圖像如圖12.
所以當k>1時,有三個交點,即方程有三個解.又x=0是方程的解,所以當k>1時,方程f(x)=kx2有四個不同的實數解.
解析2:方程的一個解為x=0.
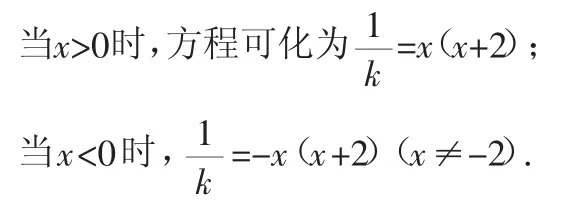
作出函數圖像不難得到正確答案.通過取倒數,把分式函數化為整式函數,使復雜函數簡單化,而且回避了漸近線,作圖就不易犯錯.
3.換元.
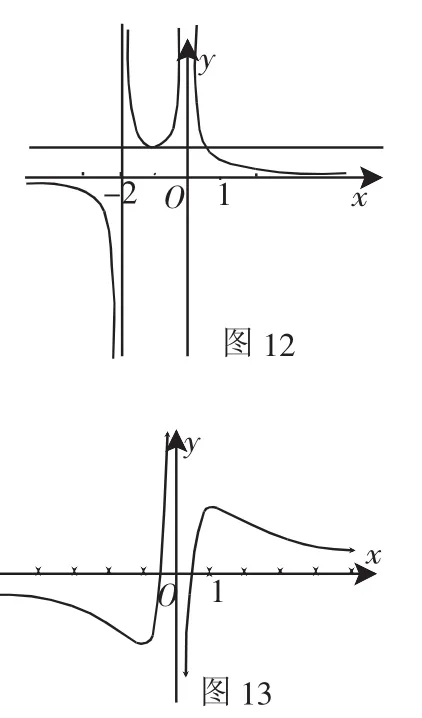
例3 討論方程ax3-3x2+1=0的解的情況.
a=0,a=±2時方程有兩解;a∈(-∞,-2)∪(2,+∞)時方程有一解;a∈(-2,0)∪(0,2)時方程有三解.
解析3:分析2雖然很直觀,但圖13還是很難畫出來的,
特別是漸近線,很容易忽略.那么能否避免呢?
函數中的漸近線問題是學生在學習函數時比較容易忽視的,本文針對此問題列舉了幾類常見函數的漸近線和處理策略.

