關于課本一道分式方程練習的思考
☉廣東省惠州市鐵路學校 陸 鋼
義務教育課程標準實驗教科書人教版八年級(下)P32題2解方程求x:
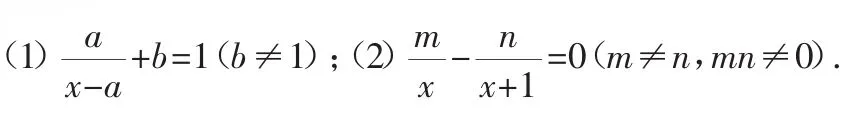
一、分式方程增根的產生原因與檢驗方法
通常分式方程是通過“在方程兩邊同乘各分母的最簡公分母”去掉分母轉化為一個整式方程(這里實際是一個一元一次方程)來求解,在這個去分母的過程中,未知數原來在分式中的取值有限制(不能使分母的值為零),到了整式中它的取值就不再受限制了,這樣就產生了所求出的整式方程的解未必恰好是分式方程的解的問題,這就是增根產生的根本原因.所以解分式方程最后都需要檢驗,這里的檢驗并不是判斷解題過程是否正確,而是要判斷所求的解是否符合要求.
在解分式方程時,當我們確信自己的求解過程沒有問題時,我們并不需要代入原方程的左、右兩邊去檢驗(可能更麻煩),我們只要代入最簡公分母(若代入后求出的值恰好為零,說明這個解會使原分式方程的某個分母為零,這樣方程中的那個分式就沒有意義,這個解就是增根,要舍去;若代入最簡公分母后,所求的值不為零,說明這個解能保證方程中各分式有意義,且使方程左、右兩邊的值相等,這個數才是分式方程真正的解).
二、分式方程解的情況探討
任何一個一元一次方程,通過去分母、去括號、移項、合并同類項等變形手段都可以化為ax=b的形式.顯然x的值是由a、b來確定的.當系數a≠0時,x有唯一值(即方程只有一個解x=;當系數a=0時,又分兩種情況:1.若b=0,即0x=0,則x可取任何實數(即方程有無數多個解);2.若b≠0,即0x=b,此時x無解.
對于含字母系數的分式方程,若去分母后轉化的是一元一次方程,它們解的關系為:1.若這個一元一次方程無解,則分式方程也無解;2.若一元一次方程只有一個解,則要進一步判斷這個解會不會使分式方程的分母為零,若使分母為零,則是增根,舍去,這樣分式方程無解了;若不會使分母為零,它就是分式方程的根,此時分式方程只一個解;3.若一元一次方程有無數個解,則分式方程也有無數個解(需說明的是這無數個解中必然存在使分式方程的分母等于零的數,也就是分式方程的增根,應排除).
三、問題的提出
課本兩道分式方程中的系數都含有字母,并且題后附加了一定的條件,大多數學生在解這兩個方程時,對條件不知道怎么用,甚至假裝“視而不見”.究其深層原因是對分式方程的解缺乏深刻理解,表層原因是只習慣于模仿性的解題,不會主動分析數量關系,缺乏理解、思考的意識與能力.事實上,不僅是學生,就是許多老師解這種題型也常常丟三落四,漏洞百出.現在我們去掉題后附加條件來探討一下這兩道方程的解的情況:
1.當b-1=0時(即b=1時):
(1)若ab-2a=0(即a=0時),則對于方程②來說x可取任意實數,即當b=1且a=0時,方程②有無數個解(含x=0),但對于方程①來說,x=0是增根,應舍去.即在b=1且a=0的條件下,方程①的解為除0外的任意實數.
(2)若ab-2a≠0(即a≠0)時,方程②無解,這樣方程①也無解.
1.當n-m=0時:
(1)若m=0(n=m=0時),方程④有無數個解(含x=0,x=-1,而這兩個對于方程③來說是增根,應舍去),所以當n=m=0時,方程③的解為除0和-1外的任意實數;
(2)若m≠0(即n=m≠0時),方程④無解,則方程③也無解.
從以上兩題的解題過程可看出,保證題1有唯一解的條件是b≠1且a≠0;保證題2有唯一解的條件是n≠m且mn≠0.然而課本在題1所附條件中就缺少了條件a≠0.
四、問題的思考
不少同學懼怕幾何題的推理論證,因為幾何證明技巧性強,變通性差,事實上代數推理比幾何推理更難掌握,更可以考查一個人的智力水平,代數題的解法通常多種多樣,只要有理,殊途同歸.學生之所以認為難,跟這方面題型“出鏡率”低,練得少有一定的關系,另外跟一些老師本身的專業素質也有關,有些老師遇到此類問題時,常常回避不講或講不清楚,學生當然就更難學好了.教師面對類似問題不應該回避,應該注意通性通法,把道理講清楚,原理講透徹.原理性的東西學生掌握了,就可以以不變應萬變,觸類旁通,舉一反三.
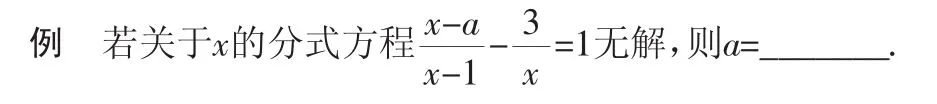
分式方程無解有兩種情況:(1)是去分母后所得整式方程無解;(2)是所得整式方程的解使分式的分母為零,即解為增根).只有學生理解了分式方程無解的道理才可能得到準確答案(a=-2或1),否則就會漏掉答案-2.
數學知識其實并不多,知識原理弄懂了,“放之四海而皆準”,很多頭腦聰明靈活的學生為什么偏愛數學,一個重要原因就是數學要記要背的東西少,花的時間少,學得輕松,容易找到成就感.作為老師,提高數學專業素養,任重而道遠.

