公式巧解涂色問題

☉江西省新干中學 胡勇彪

公式巧解涂色問題

☉江西省新干中學 胡勇彪

數列內容歷來是高中數學課程的一個重點和難點，同時涂色問題也是近年高考，甚至競賽的一個考試熱點．通過對各種涂色問題的分析，不難發現它們之間存在著某種特定的規律，下面筆者就借助于數列的線性遞推公式來巧解一類涂色問題．

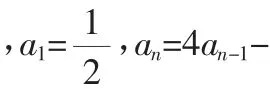
分析：題中所給出的數列遞推公式，是一類形如an+1=pan+r·qn+m（p≠1，p≠0，r≠0，m≠0）型的線性遞推公式，這種類型的數列通項一般利用待定系數法構造新的等比數列來解答，即可令an+1+x·qn+1+y=p（an+x·qn+y）化簡，與已知遞推公式對應比較，求出待定系數x和y，從而轉化為新數列{an+x·qn+y}是公比為p的等比數列，進而可求出an.

［問題拓展］如圖1，將一個圓環分成n（n≥2）個扇形區域，現用k（k≥2）種不同顏色對這n個區域染色，要求相鄰區域顏色不同，問有多少種不同的染色方法.

解：用k種不同顏色對n個區域染色，記種數為an（n≥2，k≥2）.

A1有k種染法，A2有k-1種染法，…，An有k-1種染法（不論是否與A1同色），共有k（k-1）n-1種染法，但這k（k-1）n-1種染法分為兩類：一類是An與A1不同色，另一類是An與A1同色，可看成An和A1合為一個區域，即an-1，an=（k－1）n+（－1）n（k－1）（n為區域數，k為顏色種數）.

圖1

［應用］

1.用紅、黃、藍、綠4種顏色給圖2中的A、B、C、D4個小方格涂色（允許只用其中幾種），使鄰區（有公共邊的小格）不同色，則不同的涂色方式有多少種？

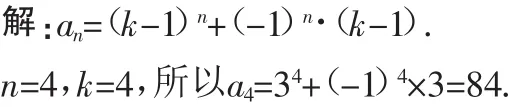
2.如圖3，在一個正邊形的6個區域中栽種觀賞植物，要求同一區域中種同一種植物，相鄰（有共同邊）的2個區域種不同的植物，現有4種不同的植物可供選擇，則共有（ ）種不同的栽種方案.

圖2

圖3

圖4

3.如圖4，一個地區分為5個行政區域，現給地圖著色，要求相鄰區域不得使用同一顏色，現有4種顏色可供選擇，則不同的著色方法共有_______種.（以數字作答）

解：對區域1著色：C14=4，然后再轉化為用3種顏色對4個圓環區域（圖5）的涂色問題．

圖5

圖6

4.（2003年全國卷理）某城市在中心廣場建造一個花圃，花圃分為6個部分（如圖6），現要栽種4種不同顏色的花，每部分栽種一種且相鄰部分不能栽種同樣顏色的花，不同的栽種方法有__________種.（以數字作答）

解：解題方法同第3題，共有120種.

5.用5種不同的顏色給圖7中的“5角星”的5個頂點染色（每點染一色，有的顏色也可以不用），使每條線段上的兩個頂點皆不同色，則不同的染色方法有_______種.

圖7

圖8

解：問題轉化為對圖8所示的5個區域著色，要求相鄰區域不同色.

6.將一個四棱錐（如圖9）的每個頂點染色，并使一條棱的兩端異色，若只有4種顏色可供選擇，則不同的染色方案有_______種.

解：由題意可轉化為圖10并進而轉化為圖11所示的著色問題.

n=4，k=3，得a4=18.

所以染色方案共有：4×18=72（種）.