讓課堂在美麗的“錯誤”中靈動起來

☉江蘇省無錫市廣豐中學 秦 嶺

☉江南大學附屬實驗中學 龐彥福（特級教師）

讓課堂在美麗的“錯誤”中靈動起來

☉江蘇省無錫市廣豐中學 秦 嶺

☉江南大學附屬實驗中學 龐彥福（特級教師）

學生在數學學習的過程中，難免會出現這樣或那樣的錯誤，學習中的錯誤常常會折射出學生在某一方面或某一知識點上存在的疑惑與困難.對于學生出現的錯誤，《義務教育數學課程標準》（2011年版）明確指出：“耐心地引導他們分析產生錯誤的原因，并鼓勵他們自己去改正，從而增強學習數學的興趣和信心”.課堂教學中學生出現的錯誤，既是課堂的生成，又是能夠充分利用的教學資源.心理學家蓋耶說過：“誰不考慮嘗試錯誤，不允許學生犯錯誤，誰就將錯過最富成效的學習時刻”.因此，在教學中我們應該理解、善待學生認知過程中出現的錯誤，并努力使不經意的錯誤轉化為寶貴的教學資源，讓課堂在美麗的“錯誤”中靈動起來，讓錯誤在課堂教學中“閃光”，進而演繹出真實課堂的無限精彩.

一、正確對待錯誤，讓錯誤成為生成資源

數學學習中的“錯誤”，就是指學生在認知過程中出現的偏差或失誤.它具有動態性、多樣性、針對性、直接性、重復性等多種特點.實踐證明，沒有錯誤就沒有經驗和教訓；沒有錯誤就沒有成功與喜悅；沒有錯誤也就沒有“吃一塹，長一智”.布魯納說：“錯誤都是有價值的”.愛迪生在上千次的錯誤嘗試后，才成功發明了電燈，這說明失敗中蘊育著成功的元素.為此，教師應該從學生的錯誤中去尋找教學的契機，努力變弊為利，使錯誤成為學生重新學習的“轉折點”、知識技能的“生長點”.學習中出現的錯誤可能是學生對所學知識沒能理解或理解不透或在認知過程中出現了偏差或是粗心大意而造成的.塞翁失馬，焉知非福.出現錯誤不完全是“壞事”，錯誤可能會成為教學中的生成，可能會成為新知識探究的起點.“糾正錯誤”更要“研究錯誤”，要研究出現錯誤的原因，要挖錯根，明錯理，做到真正認識數學、理解數學.教學中如何有效利用學生的“錯誤”資源，使課堂教學朝著有效、高效和有利于學生發展的軌道上邁進，是每一位數學教師值得研究的課題.

“生成性資源是在教學過程中動態生成的，如師生交流及生生交流過程中產生的新情境、新問題、新思路、新方法、新結果等.合理地利用生成性資源有利于提高教學的有效性”.每個人都是在錯誤中成長起來的，也是在挫折中成熟起來的.數學學習同樣是在不斷出現錯誤、認識錯誤、糾正錯誤的過程中獲得進步的.因此教師要用正確的方法引導學生正確地對待錯誤，把一次次錯誤當成課堂教與學的一次次生成，在反思中發現錯誤、分析錯誤、糾正錯誤，掌握合理的學習數學的方法，從而養成良好的學習數學的習慣.如果學生樹立了敢于正視錯誤、改正錯誤的科學態度，增強了戰勝困難的信心和意志，那么比學習數學知識本身更要有價值.

二、應對錯誤的策略剖析

1.正確理解才能正確解答

學生由于受數學活動經驗、認知水平、思維能力的限制，在學習的過程中常常會出現一些偏差或錯誤.錯誤本身并不可怕，可怕的是回避錯誤，或者簡單粗暴、不負責任地對待錯誤.教師只有根據教學目標的需要，充分合理地設計好方案，設計好恰如其分的應對措施，才能賦予“錯誤”特有的價值.“解鈴還需系鈴人”，教師切忌用自己的思想去“同化”學生，要站在學生的立場去摸清錯誤的根源，給學生提供足夠的時空，引導學生自己學會思考、分析、討論、探究，只有讓學生自己弄明白出錯的原因，并找到正確的解答方法或答案，才能使學生由衷地產生成就感，并更能自覺地投入到學習活動中，這樣，學生的錯誤才能成為“教學資源”，課堂才有可能出現精彩.

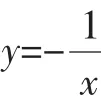
這類問題，是學生學習反比例函數時常常遇到的題目，也是認識、理解、運用反比例函數的圖像與性質過程中容易出錯的一類問題.學生看到題目，不少都搶著回答.

生1：因為k=-1＜0，所以函數y隨著x的增大而增大，于是有y1＜y2＜y3.

2.認真審題非常關鍵

學生在解題中審題不清是常有的事.比如函數中，對函數概念理解模糊，知識點掌握不牢固，解題方法不當或受題目條件的迷惑等出現這樣或那樣的錯誤.

例2 某服裝公司試銷一種成本為每件50元的T恤衫，規定試銷時的銷售單價不低于成本價，但每件不高于70元，試銷中銷售量y（件）與銷售單價x（元）的關系可以近似的看作一次函數（如圖1）.

（1）求y與x之間的函數關系式；

（2）設公司獲得的總利潤（總利潤=總銷售額-總成本）為P元，求P與x之間的函數關系式，并寫出自變量x的取值范圍；根據題意判斷：當x取何值時，P的值最大？最大值是多少？

錯解：（1）略.

答：x=75時，可獲得最大利潤6250元.

錯誤剖析：（2）在P=-10x2+1500x-50000中，

根據題意，自變量取值范圍是：50≤x≤70.

因為50≤x≤70，此時y隨x的增大而增大，

所以當x=70時，P最大值=6000.

答：略.

解答本題最大的疏忽就是審題不清，忽略了自變量x的取值范圍是50≤x≤70.數學教學要注重培養學生的思維，讓學生養成良好的學習習慣，不能丟三拉四，顧此而失彼.

3.認清實質才能透過現象看本質

曾有教學專家說過：“只有出了錯，課程才能生成.在出錯、容錯、糾錯的過程中，課堂才最活躍，才會產生多種思維的碰撞，教學才最有價值”.美國教學家在關于《基于問題的學習》一書中寫到：“在錯誤的經歷中同樣可以學到很多東西，這也是一種必要的、有意義的學習.很多時候，知道什么不行，什么不好與知道什么行，什么好一樣具有價值”.由此可見，暴露思維錯誤是糾正錯誤的前提，應是數學教學常用的策略.至于讓學生暴露錯誤的方法，則有很多.

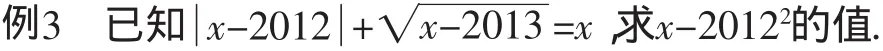
師：生1考慮的真是全面，同學們同意他的解法嗎？

絕大部分學生表示同意.

生2欲言又止.（不言，似乎又有話說）

生3：為什么出現當x=2012時，原式不成立呢？

師：解決本題的關鍵是什么？

生1：去掉題目中的絕對值符號和根號.

師：思路很正確，但如何去掉絕對值符號和根號呢？想想看，在根號中對被開方數（或式）有何要求？在去掉絕對值符號時，對絕對值內的數或代數式又有何要求？

生2：我明白了，被開方數是非負數，即x-2013≥0，得x≥2013.

生3：有了x≥2013就不用討論了，直接去掉絕對值符號，根號還是去不掉呀？

生1：噢，本題無需討論.

到這里，本題可以說是得到了圓滿解決.作為研究學習，更要引導學生學會學習，我們要進一步分析和總結，解題中受挫的原因是什么？正確解答的路徑在哪里？解決本題的突破口在哪里？關鍵在何處？這樣才能弄清楚問題的本質，《義務教育數學課程標準》（2011年版）倡導“要注意培養學生良好的數學學習習慣，使學生掌握恰當的數學學習方法”.

實踐證明，不出錯的學生，未必就是最有智慧的學生；不出錯的教學，未必是真實的教學；不出錯的課堂，未必就是最好的課堂.其實，錯誤往往是學生思維、認知、經驗最真實的暴露.筆者堅信，錯誤是正確的先導，是通向成功的階梯，是教和學珍貴的財富資源；錯誤是達到真理的一個必然環節.只要我們多關注學生在學習過程中出現的錯誤，多關注學生獨特的感悟，用“點石成金”的慧眼去發現學生錯誤中的教學價值，用“指點迷津”的睿智去化解、點撥學生的錯誤，“錯誤”就一定會成為促進學生增長知識、豐富情感、發展思維最有效的教學資源，教學就會變得更加靈動、更加精彩、更加厚實、更為有效.

1.任仕忠.中學數學解題糾錯實用寶典（初中分冊）［M］.西安：陜西師范大學出版總社有限公司，2011.

2.姜鴻雁，龐彥福.好鋼用在刀刃上——結合解題教學淺談課堂時間的有效利用［J］.中學數學，2013（1）.

3.龐彥福.教師寫作的素材從哪里來［J］.中學數學教學參考（中旬），2012（10）.

4.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.