重視發展思維能力，促進數學有效教學

何文娟

數學是思維的體操，是思考的學問。而思維是數學有效教學的核心。在中學數學教學中，怎樣提高學生的思維能力？

一、大膽猜想，自由探索

數學猜想是一種創造性的數學思維活動，是培養學生創新能力的重要途徑。在教學過程中讓學生大膽猜測、假設，提出一些預見性的想法，設想對事物的瞬間頓悟，有利于學生創造性思維的發展。

比如完全平方公式（a+b）2的學習，先引導學生猜想，在錯誤的猜想結果a2+b2的基礎上引導大家計算得出最后的公式（a+b）2=a2+2ab+b2。雖然猜想錯了，但學生興致很高，并進一步猜想（a+b）3=a3+3ab+b3，這時學生沒有盲目相信自己的猜想，而是進一步驗證出最后的結論： （a+b）2=a3+3a2b+3ab2+b3。雖然前面的兩次猜想錯了，但大家能更理智地通過它們的特點進一步猜想 （a+b）n，從系數、項數、字母的指數等方面展開了猜想的翅膀，最難的就是系數的規律，個別積極思考的學生把（a+b）n的指數n為1、2、3、4時的展開式的系數列成了表

1

11

121

1331

14641

我興奮地告訴學生他們發現了我國古代數學家發現的重要規律——楊輝三角，真的了不起，這是大家樂于思考、善于猜想的結果。

二、鼓勵求異，大膽求知

求異思維是主體面臨問題時，能從多角度、多方位思考問題，使思路由一條擴展到多條，由一個方向轉移到多方向的思維方式。求異思維與創新能力有著直接的關系，是創新思維的核心。數學課上教師應多設計一些活動空間，引導學生打破常規思維的束縛，憑借自己的智慧和能力積極地從不同途徑、不同角度去思考問題，為學生提供創造空間，提供創造機會，培養創造能力。

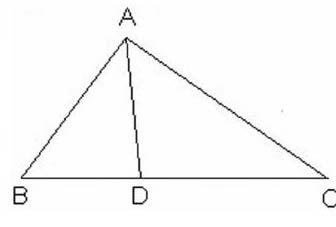
例如三角形角平分線性質定理：如圖，AD為△ABC內角平分線，求證：=。

很多教師在碰到這類題目時，只是機械地要求學生記牢、會運用這個結論就可以了。但我認為這道題目的證明過程實質是眾多知識的運用和反映，應花大力加以證明和引導，要求學生盡可能多地運用各種方法證明。多數學生會考慮構造相似三角形的基本圖形——“八字型”“塔型”。

三、變式訓練，激活思維

任何一個數學問題的解答思維過程，一般地都可以把它分解為三個基本部分：問題的條件部分、問題的解答過程、問題的結論部分。如果把這三個部分作為變化的因素，可以構成條件變式題、結論變式題、過程變式題。在進行變式題設計時，應主要依據教材的例題與習題。

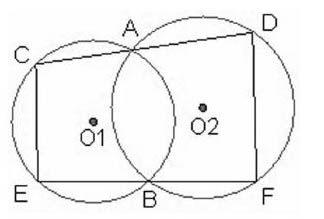
例如，“圓內接四邊形”一節的例題是：⊙O1與⊙O2都經過A、B兩點，經過A點的直線CD交⊙O1于點C，與⊙O2交于點D，經過點B的直線EF與⊙O1交于點E，⊙O2交于點F，求證：CE∥DF.在此題基礎上，可得條件變式題：①已知CD∥EF，求證四邊形CEFD是平形四邊形；②已知CD∥EF，求證CD=EF.經過如此分析，對培養學生識圖、證明的能力是有益的，并且起到了鞏固“雙基”的作用。

在變式教學中應該強調變式題的設計與訓練。遵循學生的認識規律和年齡特征，按照由低到高，由淺入深的原則，設計階梯度清晰的各類變式題組，加強對學生的訓練；注重精講多練（變式訓練），充分發揮教師的主導作用，學生的主體作用和訓練的主線作用。在實施變式教學方法的同時，應注意針對不同的內容，不同的教學階段使用不同的教學方法。如復習課教學，就可以采用“定向—自學—點撥—自測—評講—自結”程序的方法，對培養學生能力，實現教學目標，提高課堂效益會起到理想的教學效益。

四、開放教學，發散思維

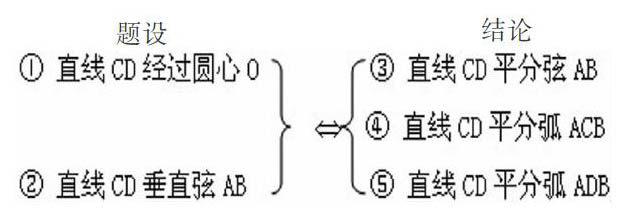
課本在許多地方給我們安排了絕佳的開放問題的內容，例如：垂徑定理用其推論的內容繞口且不易分辨清楚，如果將題設的結論用下列方式理順并由此展開開放式討論，學生的掌握情況要好得多。如果把題設和結論中的5個條件適當互換，又會如何？

讓學生作為主體，討論這個開放式問題，不難得到：對于一個圓和一條直線來說，如果以上5個元素中的任何兩個作為題設成立，則其它3個作為結論也成立。這樣可得到垂徑定理的9個推論。

此外，還有圓心角、弧、弦、弦心距的關系定理、弦切角定理的證明等。把它們當開放問題處理都能取得很好的教學效果。

責任編輯 羅峰