線性代數課程教學質量之探討

曾友芳

[摘 要]本文在闡述線性代數課程在大學教育中的重要性之后，探討了在教學過程中如何提高教學質量的問題。從備課、課堂教學、課后跟蹤到考前模擬，每個環節都根據實際情況制定相應的實施方案，任課老師因材施教，因學生而異進行管理和輔導，跟蹤學生的學習效果，從而使學生獲得真才實學的內在質量提升和期考好成績乃至能將所學應用于實際的外在效果。

[關鍵詞]線性代數 教學質量 因材施教

[中圖分類號] G421 [文獻標識碼] A [文章編號] 2095-3437（2013）08-0073-03

線性代數是高等院校大部分專業必修的一門公共數學課程，其應用范圍廣泛，如微分方程、運籌學與控制論等數學分支，計算機圖形學、計算機輔助設計、密碼學等技術，無不以線性代數為其理論研究和算法設計的一個重要基礎組成部分。在電氣、土木、金融等領域，很多實際問題的數學模型是含有多個變量多個約束的優化問題，而求解這些問題就必須有線性代數的基礎，才能理解相關的更深理論，如線性規劃、非線性規劃等的算法和理論，最終利用計算機依據算法編程來求解相應的數學模型，以此得到最優解。

美國著名數學教育家、美國國家“線性代數課程研究小組”的核心成員、線性代數課程現代化的主要倡導者David C.Lay 教授在其著作《線性代數及其應用》中述及：“這門課程是最有趣、最有價值的大學數學課程。事實上，一些學生在畢業以后告訴我他們在大公司的工作中或工程研究生院的學習中還使用本教材作為參考書。”[1]誠如其所言，不少研究生在專業研究中將以線性代數的知識作為基礎工具，如果沒有本科學習時打下的扎實基礎，要想使用其以提升自己的論文質量和研究成果，甚至只是進一步的學習，那么這將是制約發展的瓶頸。比如最優化中的線性規劃[2]，就以線性代數知識為基礎，而金融[3]、工程[4，5]等許多領域的應用中要用到最優化的知識，這樣基礎中的基礎問題——扎實掌握線性代數知識，其重要性不言而喻。

然而，另一方面，線性代數具有高度的抽象性和嚴密的邏輯性，概念多， 定理多，易混淆， 計算繁瑣，這使許多學生認為線性代數是一門抽象難懂的課程，不易掌握，望而卻步，但其廣泛的應用性卻激起了學生們強烈的學習需求，如何解決這個矛盾是教師一直在思考的問題。筆者在高校任教，經過教學實踐，不斷改革探索，教學質量穩步提高。在此和同行探討這一問題，以求進步。

一、備課面廣泛且要因材施教

備課不僅要備教材內容，而且還要根據學生學習情況和需要準備相關的改進提高措施。以同濟大學《線性代數》第五版的教材為例，一般授課的主要內容是第一到第五章，即行列式、矩陣及其運算、矩陣的初等變換與線性方程組、向量組的線性相關性和相似矩陣及二次型，課時為45節，每節40分鐘，按這個時間來安排好教學是比較緊張的。“如何安排好全程教學、提高教學質量、達到優質的教學效果？”就是一個擺在任課教師面前的重要問題。

俗話說：臺上一分鐘，臺下十年功。老師要想教好學生，給每個學生一碗水，自己就得有一桶水，所以老師就要在備課階段下足工夫。首先，研究教材，了解重難點，還有整個授課內容的框架和內在脈絡，這些都要了如指掌，為透徹理解這些理論及其應用，建議多讀國內外經典教材和教輔書，如參考文獻[1]等。其次，為豐富教學內容，提高學生學習興趣，學習對課堂整體把握的技巧等，廣泛閱讀教改論文，尤其是近幾年的論文，了解關于線性代數課程的現狀、發展和局限，學習同行如何提高學生的學習興趣[6]，如何在課堂上滲透數學思想以提高學生的數學素養[7]等。再次，查看國外著名的大學公開課線性代數的教學視頻，國內精品課程網站，認真學習名師的網上課堂，通過對教學大綱的了解和比較，調整原來的重難點，平時抽空走進教學名師的課堂，親身感受名師風采，總結差距，調整自己的授課布局和方法。最后，綜合考慮本學期授課學生的專業特點，汲取網上課件制作中的精華，調整修改制作課件。

二、提高課堂質量

每次上新課前，先將上次課講授的重難點讓學生回顧一下，看看還有哪些學生沒理解掌握的，加以引導，尤其是主線脈絡，順此理清，承上才好啟下。講授新課前先說明需講授的要點分別是哪幾點，這幾點的關系等，然后再逐一展開。因為線性代數的概念和知識點較多，所以講授過程中分段總結很重要，某個知識點要么在引例中看其用處，要么講完后通過應用或故事說明它的用處或將在哪些方面應用，以拓展學生的思路和知識面，并提高學生的學習興趣，等用到的時候又再強調回顧。

同時，知識點間的聯系與比較都可以反復進行，比如矩陣和行列式的不同與相似，概念和記號不同，但行列式的某些性質和矩陣的初等變換有類似之處，啟發學生“如何通過比較巧妙記憶”；在判斷齊次線性方程組是否有非零解時，一般將系數矩陣化成階梯形后，根據矩陣秩與方程組中含有未知數個數的比較來判斷，但當系數矩陣是低階或易于計算其行列式的方陣時，簡單計算系數行列式，由其為零即可知此齊次線性方程組有非零解。學習新知的過程就是反復復習的過程，以此減輕學生的課后學習負擔，同時也可以檢測學生對已學內容的掌握情況，如此推進，學生在這個過程中就可以把知識脈絡框架建立起來，從而熟悉自己的課本，熟悉所學內容，做練習才得心應手，并且印象深刻，等到后續課程需要這些知識時，可以很快地回憶起來而應用于實踐。

三、課后追蹤練習情況

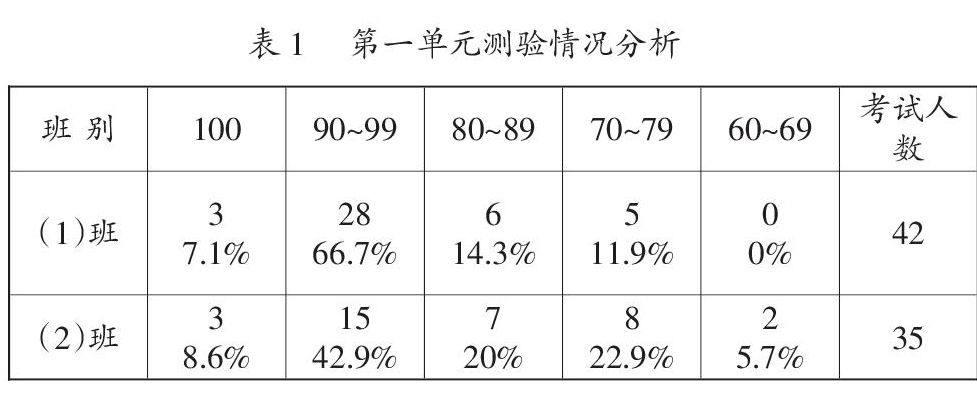
每次課后，讓學生做與授課知識點相關的練習，原則上學習完一章就進行單元測驗，題型主要可分為填空題、選擇題、判斷題、計算題和證明題。填空題考核學生對基礎知識的掌握；選擇題考查學生靈活應用知識的能力；判斷題考核學生對概念、定理、性質等理論的掌握和辨析能力；計算題考核學生的計算能力和綜合能力，證明題考核學生對一些重要定理的認知和應用能力。一般設置單元測驗的時間是40分鐘，即1小節課，可隨堂測驗也可另作安排。測驗后仔細批改，記錄常見錯誤的情況，如某道計算題，學生常見的錯誤有幾處，每處是哪些情況。講評時重在正面講授，講清關鍵點和思路、做題步驟、錯誤情況等。以教學過程中遇到的由兩個專業班級合成的教學班為例，每次列表比較班級的考分情況，如下表1：

這對激起學生的學習斗志有催化劑般的作用。通過這樣的比較，每次兩個班都在暗暗較量，并且每個學生經過講評和更正都知道自己的改進方向，待到期考，大部分同學都有明顯的進步，甚至原來測驗落后的班級會取得突出的成績，比如，這里的（2）班，期考35人中僅有1人卷面分（滿100）不及格（56分），但（1）班因一直占優勢，沒有居安思危，所以還有3位學生不及格。

另外，適時的在課后安排幾次輔導答疑時間，可要求學習有一定困難的學生參加，其他學生不做要求。重點抽查學生完成作業及批改后的作業、測驗改錯情況，看看他們對錯題是否理解清楚、是否更正。再則詢問他們對知識點是否掌握，可通過讓他們講述典型例題的方法了解他們的思路是否正確清晰。之所以要如此細致追蹤，是因為當前的大學新生剛由中學轉入，有些還是很依賴老師的管束，不夠自覺，盡管老師可以在課堂的教學中一再說明要自主學習，但部分學生自制力還待逐步提高，還需要老師的適時幫助，否則這部分學生將會跟基礎好及主動性強的學生拉開更大的差距，到期考前臨陣磨槍就肯定來不及了。

四、考前總復習

期考前，也就是最后一次課，一般會對課程進行總復習，此時再強調，課本內容為主，其他練習為輔。通過練習真正理解課本的理論知識，而不是本末倒置，只顧練習而不重課本理論，練得一題算一題，不知道總結也不知道課本的重心在哪兒。可以分章節講重點，弄清每章的綜合計算題方向，因為大部分重難點都集中在這些題中考核，比如：求解矩陣方程，就考核了矩陣的逆的存在和計算，矩陣的加法、減法和乘法的運算，以及因矩陣乘法的交換律不一定成立而需考慮的左乘右乘問題等。再如，將二次型用正交變換法化為標準形，就涉及二次型對應的矩陣的特征值和特征向量的問題，而求解特征向量又是一個個解線性方程組的過程，其間還有將特征向量正交單位化的處理。由此層層分析后，特別強調其中的一個基礎計算——將一個矩陣化成階梯形和最簡形的計算——一定要過關，否則后續大部分計算題將無法完成，因為它們都以此計算為關鍵的一步。

經過整個環節的把握，只要學生不是刻意不學，一般來說都能順利通過期末考試，半數左右的學生可以通過自身的加倍努力取得80分以上的優良成績，以筆者近一年兩個學期所帶的非數學專業班級參加全校統考（考教分離）成績結果為例，如表2可以看到改進后的較精細化教學方法帶來教學質量穩步提升的效果。

[ 參 考 文 獻 ]

[1] David C.Lay 著，劉深泉等譯. 線性代數及其應用（原書第3版）——華章數學譯叢[M].北京：機械工業出版社，2005.

[2] Mokhtar S.Bazaraa，John J.Jarvis and Hanif D.Sherali. Lin？鄄ear Programming and Network Flows（the Fourth Edition）[M]. Canada：John Wiley & Sons Canada，2010.

[3] 宋威. 金融數學模型[M].廣州：華南理工大學出版社，2005.

[4] 鄭國強，鮑海，陳樹勇. 基于近似線性規劃的風電場穿透功率極限優化的改進算法[J]. 中國電機工程學報，2004：68-71.

[5] 耿紅，王澤民.基于灰色線性規劃的土地利用結構優化研究[J]. 武漢：武漢測繪科技大學學報，2000，25（2）：167-171，182.

[責任編輯：左 蕓]