高職數學教學內容的探討

王燕

摘 要： 隨著科學技術的飛速發展，教育的發展面臨巨大的挑戰，這對高職數學課程的教學提出了新的要求。本文分析了高職數學教學中存在的問題，并提出了相應的解決策略。

關鍵詞： 高職數學教學 教學內容 基礎知識

在當今知識經濟時代，教育對社會的發展起到越來越重要的作用。近年來，高職教育迅速發展，為社會輸送了很多高級技術應用型專門人才。數學是自然學科中的基礎學科，是高職教育中必不可少的課程，一方面為學生后繼學習做好了鋪墊，另一方面對學生思維的發展具有重要意義。

一、高職數學教學現狀

1.教學起點高，學生數學素質低。

高職數學以一元微積分為基礎模塊，根據不同專業情況，選擇微分方程、概率與統計、積分變換等作為拓展內容。這些對學生的已有知識、思維能力、學習能力都有一定的要求，但高職學生的實際狀況與此要求存在較大差距。有的學生初等數學的知識沒掌握好，沒有養成良好的學習習慣。有的學生剛進校時學習熱情高漲，不久就歸于消沉，覺得自己學不好數學。

2.部分數學老師經驗不足。

剛入職的高職數學教師對學生所學專業大多了解不夠，授課時大部分講解理論，比較抽象，僅憑對數學的基本認識備課、講課，忽視實際應用。

3.教學內容多，教學課時少。

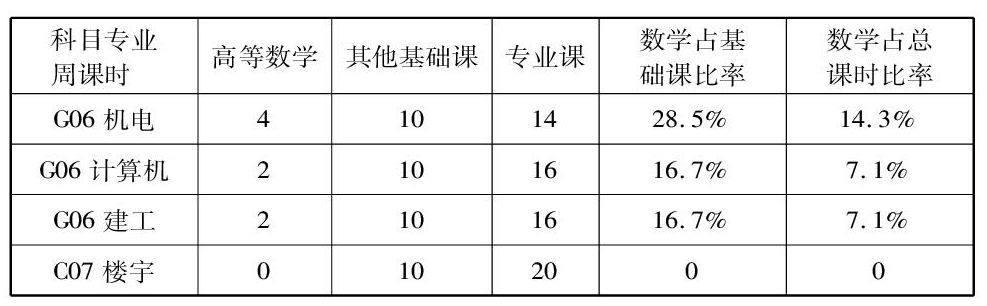
高職數學一般只在第一學年開課，每周四至六課時，而按照學校開學慣例，一年級新生在第一學期要晚3周（約占學期的六分之一）才正式上課。所以，無論選擇什么樣的教材，都要壓縮教材內容而趕進度，結果影響了教學質量，增加了學生的學習負擔。以下為某一學校數學課時、專業課的安排表：

從表中可以看出部分專業的數學課時所占比例相當小，這也是高職院校數學教學中普遍存在的問題。

二、改變高職數學教學現狀的策略

1.界定數學教學內容。

當前高職數學教材涉及的教學內容是相當廣泛的，有一元微積分及其應用、多元尤其是二元微積分及其應用、常微分方程、線性代數等基礎知識，還有概率統計及數學軟件實驗等知識，符合高職院校的應用性準則。數學教師對高職數學內容及講解的程度應做好界定。

（1）概念和定義是區分事物的根本，也是事物本身的性質、與眾不同的地方。在教學中必須強調對概念的理解，使學生一聽到這個概念就知道它的本質，并且能聯系其他與之相關的結論及一些應用實例，至少能用一個例子對此概念進行分析。如說到一元函數，就能準確地描述其定義：變量、集合和對應法則，進而可以想到它們的應用，比如復利、信號波等。

（2）合理權衡對定理的證明和公式的推導。定理的證明，在很大程度上都是概念的應用和理解，如在講解完一元函數的導數之后，可讓學生根據導數的定義式推導具體函數，如對數函數的導數。這樣，既能加強學生對導數概念的理解，又能提高學生的動手能力和思維能力。

（3）注重數學知識的實際應用，增強學生自身對數學的親近感。比如，在講一元函數的導數時，重點應放在導數的實際意義上，讓學生知道函數變化率在日常生活和生產中是經常碰到的，如人口出生率、電流強度變化率等。這樣，學生會覺得數學很有用，有趣，自然就產生了學習興趣。

2.必須掌握基礎知識。

高職數學是以變量為研究對象，初等函數是連接初等數學與高等數學的紐帶，極限則是高等數學研究函數重要思想方法。極限的概念和思想在高等數學中占有重要的地位，它的思想、方法貫穿高等數學的始終。極限是人們研究許多問題的工具，這些問題涉及從有限中認識無限、從近似中認識精確、從量變中認識質變的過程。可以適當地將“ε-N語言”和“ε-δ語言”介紹給學生，讓他們對離散和連續的概念有所了解，還可根據實際問題構造函數，因為學生以前接觸過極限，接下來就需對極限作深層分析，強調應用極限思想求極限的前提條件等細節問題，這對培養學生嚴密的思維是很有益的，有助于對后面函數導數和積分的理解。其次，一元函數的導數、微分和積分也需作為重點內容加以強調。微積分中的許多思想方法對于學生思維方式的形成和思維能力的訓練都起到十分重要的作用，無論將來學生畢業后從事何種工作，微積分的數學思想方法都是不可或缺的。另外，多元函數微積分對于培養學生空間思維和對事物的歸納推理總結能力具有重要意義。這部分理論可以用與一元函數相關結論比較的方法來進行拆解，注重加深學生對微元法及變分法的理解，從而對函數的微分及積分的概念有更深的理解，對微分和幾何的結合有更深層的認識。

以上是絕大多數高職學生，尤其是理工類專業學生，必須掌握的數學知識。如果課時充足，還可以適當補充數學軟件應用方面的知識。更重要的是，要使學生在學習、理解這些知識的同時，懂得遇到實際問題應如何思考才能正確地解決問題，這也是高職數學教育的目標。

參考文獻：

[1]曹之江.數學分析基礎原理[M].呼和浩特：內蒙古出版社，2004.

[2]程其襄，張奠宙，等.實變函數與泛函分析基礎[M].北京：高等教育出版社，2003.

[3]王凌云.論高職院校高等數學教學應該突出的幾個問題.山東師范大學學報，2008，9，VOL23（3）：134-136.