從不同視角探求一道課本習題中“視角”的最值問題

●韓慶文 (滕州市第一中學 山東滕州 277500)

普通高中課程標準實驗教科書(人教A版)《數學》必修5習題3.4中的B組第2題如下：

題目如圖1，樹頂 A離地面a m，樹上另一點 B離地面b m，在離地面c m的C處看此樹，離此樹多遠時看A，B的視角最大?

分析由于在C處看A，B的視角為∠ACB，對于這一問題我們既可以從幾何的角度審視，也可以從代數的角度審視.

圖1

從平面幾何的角度考慮，可以借助于圓的有關性質.

視角1 如圖2，過點C垂直于AB的直線記為DE(D為垂足).當DE與過點A，B的圓相切時，切點記為C，此時∠ACB=∠α最大.

事實上，觀察圖2，易得無論點C是前行還是后退到點C'，過點A，B，C'的圓必與直線DE相交，此時∠AC'B必小于圓內的∠α.當DE與過點A，B，C的圓相切且切點為C時，由切割線定理得

圖2

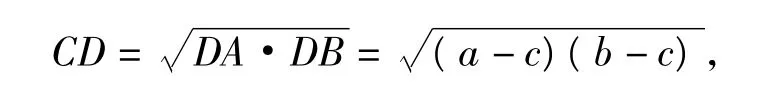
視角2 (借助于兩角差的正切公式求tan∠ACB的最大值)

圖3

視角3 (借助于正弦定理求sin∠ACB的最大值)

由視角2可得

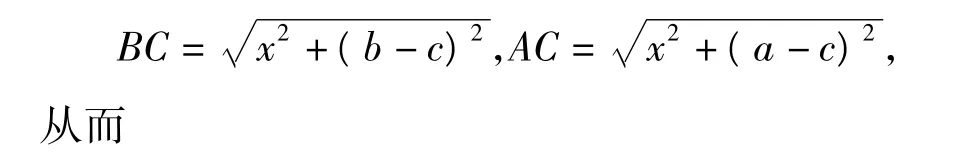
視角4 (借助于余弦定理求cos∠ACB的最小值)

由視角2可得

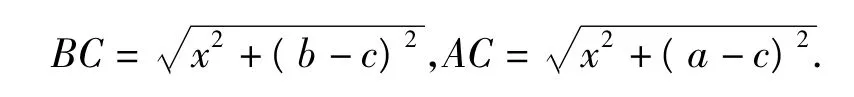
又AB=a-b，在△ABC中，由余弦定理得