中間索面斜拉橋并列拉索尾流馳振數(shù)值研究
馬如進(jìn),倪美娟
(同濟(jì)大學(xué) 橋梁工程系,上海 200092)
拉索是斜拉橋的關(guān)鍵構(gòu)件,由于其剛度小、阻尼低、質(zhì)量小的特點(diǎn),在風(fēng)荷載作用下極易發(fā)生不利振動(dòng)。斜拉索的振動(dòng)類型較多,包括風(fēng)雨激振、參數(shù)共振、渦激振動(dòng)、抖振、馳振等等。斜拉索大幅的振動(dòng)容易引起錨固端的疲勞,損壞腐蝕保護(hù)系統(tǒng),縮短拉索的壽命。近年來(lái)中間索面斜拉橋受到了廣泛青睞,在我國(guó)就有十幾座中間索面的斜拉橋,如濟(jì)南建邦黃河大橋、寧波大榭二橋、珠海淇澳大橋和武漢后湖大橋等。對(duì)于中間索面斜拉橋而言,由于兩索面間距很近,并列拉索的尾流馳振則成為橋梁設(shè)計(jì)過(guò)程中應(yīng)該關(guān)注的重點(diǎn)問(wèn)題。
馳振是一種空氣動(dòng)力失穩(wěn)現(xiàn)象,它是具有特殊斷面形狀的細(xì)長(zhǎng)結(jié)構(gòu)物在垂直氣流方向表現(xiàn)出的一種大幅度振動(dòng)現(xiàn)象,其振動(dòng)頻率遠(yuǎn)低于相同截面的漩渦脫離頻率,這種振動(dòng)最先發(fā)現(xiàn)于結(jié)冰的電線,振動(dòng)激發(fā)的波在兩根電線之間的振幅可達(dá)電線直徑的10倍[1]。而尾流馳振則是兩根沿風(fēng)向斜列的拉索,在來(lái)流方向下游的拉索表現(xiàn)出比上游拉索更強(qiáng)烈的一種發(fā)散振動(dòng)。近年來(lái)國(guó)內(nèi)外學(xué)者對(duì)于斜拉索尾流馳振做了不少研究,Tanaka[2]指出尾流馳振可能發(fā)在兩斜拉索相距很近的情況,也可能發(fā)生在兩斜拉索相距很遠(yuǎn)的情況,兩索間距可分為近距失穩(wěn)區(qū)、穩(wěn)定區(qū)及遠(yuǎn)距失穩(wěn)區(qū)。國(guó)內(nèi)學(xué)者[3~5]對(duì)于影響并列索的因素研究基本集中在索間距、風(fēng)偏角、風(fēng)攻角、固有頻率等,國(guó)外學(xué)者[6~7]對(duì)上游索的約束條件、模型的對(duì)數(shù)阻尼衰減率、折減風(fēng)速大小的影響等方面也做了較多的研究。陳志華等[8]對(duì)于斜拉橋的幾種典型振動(dòng)做了總結(jié),認(rèn)為:尾流馳振受拉索間距的影響非常明顯,尾流馳振產(chǎn)生的條件為拉索的中心距在1.5~6的拉索直徑。
斷面發(fā)生馳振的主要原因在于升力系數(shù)存在負(fù)斜率,而圓形索截面的升力系數(shù)為零,不可能出現(xiàn)升力系數(shù)的負(fù)斜率,因此也不會(huì)發(fā)生馳振現(xiàn)象。但對(duì)于并列拉索而言,由于兩根索相距較近,在風(fēng)作用下存在較明顯的氣動(dòng)干擾現(xiàn)象,其氣動(dòng)力系數(shù)必然與單根拉索不同。本文以某中間索面斜拉橋?yàn)槔ㄟ^(guò)數(shù)值模擬技術(shù)獲得并列拉索的靜氣動(dòng)力系數(shù)及其隨攻角的變化規(guī)律,在馳振的判別原則的基礎(chǔ)之上開(kāi)展尾流馳振的判別方法和發(fā)生風(fēng)速研究,并進(jìn)一步通過(guò)針對(duì)拉索阻尼比、拉索振動(dòng)頻率等參數(shù)分析,分析了拉索尾流馳振發(fā)生風(fēng)速,研究方法可為類似橋梁所參考。
1 尾流馳振的分析方法
經(jīng)典馳振理論[1]認(rèn)為馳振基本由準(zhǔn)定常力(將氣流看作是定常的氣動(dòng)自激力理論)控制的,均勻流流過(guò)細(xì)長(zhǎng)體斷面的豎向振動(dòng)方程為:

式中:m為質(zhì)量(kg/m);y為橫風(fēng)向的振動(dòng)位移(m);ζ為結(jié)構(gòu)阻尼比;ω為橫風(fēng)向振動(dòng)圓頻率(Hz);ρ為空氣密度(kg/m3);U是風(fēng)速的水平分量(m/s);B為梁寬(m);CL為升力系數(shù);α為攻角(°);CD為阻力系數(shù)。

顯然,至少要:

時(shí)才會(huì)出現(xiàn)馳振不穩(wěn)定現(xiàn)象,這就是著名的鄧哈托判據(jù)。式(3)的左端又稱為馳振力系數(shù),由此馳振臨界風(fēng)速的估算公式則為:
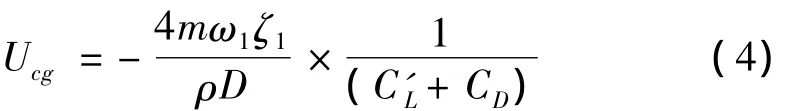
式中:C'L為升力系數(shù)對(duì)攻角的斜率,C'L=dCL/dα。
對(duì)于并列斜拉索而言,處于下游的拉索,在面內(nèi)振動(dòng)過(guò)程中所受到的靜氣動(dòng)力系數(shù)在不斷變化,當(dāng)拉索偏離風(fēng)軸時(shí)的靜氣動(dòng)力系數(shù)可以通過(guò)模擬并列拉索在不同風(fēng)攻角下的靜風(fēng)荷載獲得,如圖1所示。圖中D為拉索直徑,H為拉索中心距,α由于風(fēng)向引起的風(fēng)攻角,F(xiàn)L與FD分別為拉索的升力系數(shù)與阻力系數(shù)。
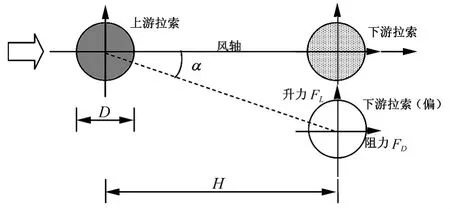
圖1 并列拉索風(fēng)荷載模擬示意圖Fig.1 Schematic diagram of wind loading simulation for parallel cables
2 并列拉索的數(shù)值模擬
本文以某已建成的中間索面斜拉橋?yàn)槔_(kāi)展研究,該橋拉索水平間距1.2 m。拉索的直徑165 mm~240 mm,拉索水平間距約為拉索直徑的5~7.3倍,如圖2所示。并列拉索的數(shù)值模擬選擇直徑為180 mm的拉索作為研究對(duì)象,由此可以推算出拉索間距為拉索直徑的6.67倍。

圖2 中間索面斜拉橋主梁拉索橫斷面圖Fig.2 Cross sections of deck and cables of the cable stayed bridge with central cable plane
根據(jù)陳政清[4]、劉慕廣[5]等的研究成果,在 15°攻角附近容易發(fā)生尾流馳振,因此本文選擇攻角范圍-24°~+24°。數(shù)值模擬采用大渦數(shù)值模擬方法[10]進(jìn)行,由此可以得到不同風(fēng)攻角下的并列拉索的流場(chǎng)分布及靜風(fēng)荷載系數(shù),如圖3和圖4所示,其中拉索的阻力系數(shù)與升力系數(shù)的定義如下:
阻力系數(shù):
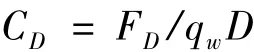
升力系數(shù):

由分析結(jié)果可以發(fā)現(xiàn),并列拉索在橫風(fēng)作用下,處于上游拉索的阻力系數(shù)基本保持不變,即0°風(fēng)攻角時(shí)為0.862,隨著風(fēng)攻角增加逐漸下降到0.8左右;而處于下游的拉索在0°風(fēng)攻角時(shí)阻力系數(shù)最小為0.194,隨著風(fēng)攻角的增大阻力系數(shù)逐漸增加。可以發(fā)現(xiàn),當(dāng)并列拉索處于正橫風(fēng)向時(shí),受上游拉索的阻擋效應(yīng),下游拉索的阻力系數(shù)明顯降低。
對(duì)于升力系數(shù)而言,在橫風(fēng)作用下隨著風(fēng)攻角的增加,上游拉索的升力系數(shù)出現(xiàn)負(fù)值,即受下游拉索的影響,上游拉索有向下游拉索靠攏的趨勢(shì),這種趨勢(shì)隨著風(fēng)攻角出現(xiàn)先增加再減小的趨勢(shì)。對(duì)下游拉索而言,升力系數(shù)的變化較為復(fù)雜,在風(fēng)攻角較小的情況下,升力是由下游拉索向上游靠攏,但隨著攻角的增加,又表現(xiàn)為一種斥力,當(dāng)攻角繼續(xù)增加,該力則逐漸降低。

圖3 14°風(fēng)攻角流場(chǎng)顯示Fig.3 Flow field at wind attack angle of 14°

圖4 并列拉索的靜氣動(dòng)力系數(shù)Fig.4 Static coefficients of parallel cables
3 拉索尾流馳振發(fā)生風(fēng)速
由數(shù)值模擬結(jié)果可以發(fā)現(xiàn),對(duì)于上游拉索與下游拉索都存在升力系數(shù)的負(fù)斜率現(xiàn)象,因此需要對(duì)升力系數(shù)的斜率進(jìn)行分析,如圖5所示。由斜率曲線可見(jiàn),對(duì)于上游拉索出現(xiàn)的負(fù)斜率最小為-0.72,考慮上游拉索最小的阻力系數(shù)也大于0.8,因此上游拉索不具備發(fā)生馳振的條件。
處于下游的拉索,升力系數(shù)最大的負(fù)斜率發(fā)生在15°~17°附近,可以達(dá)到 -3.767,而在相應(yīng)風(fēng)攻角下的阻力系數(shù)僅為0.411,則馳振力系數(shù)為-3.356,可見(jiàn)下游拉索發(fā)生馳振失穩(wěn)的可能性很高。

圖5 并列拉索的升力系數(shù)斜率Fig.5 Slope of lifting coefficients of parallel cables
對(duì)于本文的中間索面斜拉橋而言,最長(zhǎng)拉索(MC26)的一階面內(nèi)振動(dòng)頻率為0.70 Hz,可以根據(jù)式(2)進(jìn)行馳振穩(wěn)定性發(fā)生風(fēng)速分析,并取拉索自身阻尼比為0.1%,馳振力系數(shù)取最不利值 -3.356,ρ取為1.225 kg/m3。通過(guò)分析可以得到馳振發(fā)生臨界風(fēng)速如表1所示。可見(jiàn),當(dāng)拉索阻尼比為0.1%時(shí),拉索發(fā)生尾流馳振的風(fēng)速較低,因此下游拉索發(fā)生尾流馳振的可能性較高。同時(shí)可以發(fā)現(xiàn),對(duì)于長(zhǎng)索由于其頻率低,尾流馳振發(fā)生風(fēng)速也相對(duì)較低。
對(duì)于不采取任何措施的斜拉索其自身的阻尼比約為0.1%。然而,對(duì)于大跨徑斜拉橋而言,為了降低拉索在風(fēng)作用下的不利振動(dòng),一般采用各種提高拉索系統(tǒng)阻尼的措施,如索端阻尼器、油壓阻尼器、粘滯阻尼器等等。通過(guò)對(duì)拉索阻尼比的參數(shù)分析可以發(fā)現(xiàn),拉索阻尼比的提高可以顯著提高尾流馳振發(fā)生風(fēng)速。
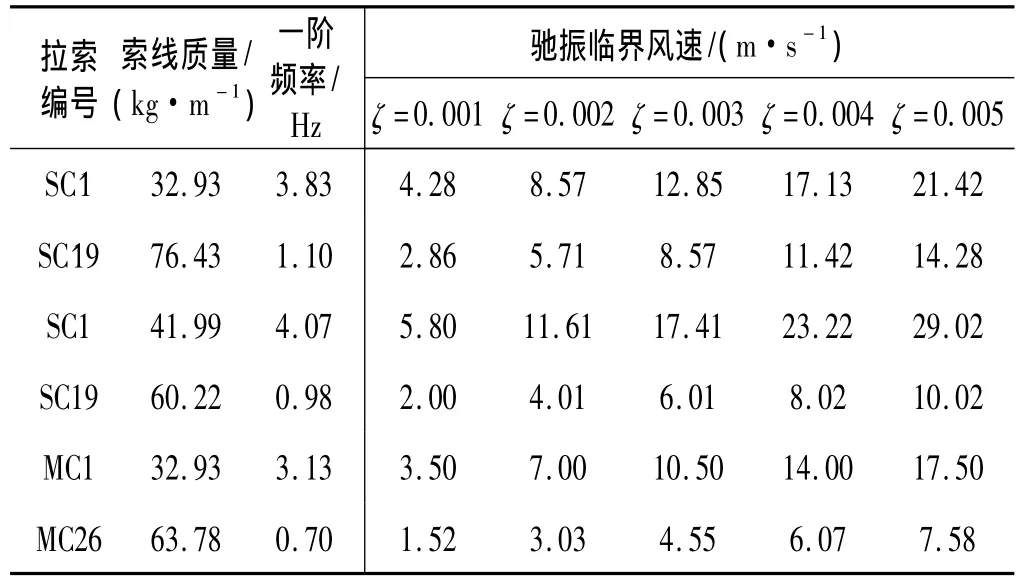
表1 阻尼比對(duì)馳振臨界風(fēng)速的影響Tab.1 Galloping critical wind speed vs.damping ratios
由上表分析結(jié)果不難發(fā)現(xiàn),即使在拉索系統(tǒng)阻尼比達(dá)到0.5%的水平,對(duì)于長(zhǎng)索的尾流馳振發(fā)生風(fēng)速仍然處于一個(gè)較低的水平,因此必須采取適當(dāng)?shù)拇胧┨岣唏Y振發(fā)生風(fēng)速。針對(duì)拉索尾流馳振的控制措施,較通常采用的方法是在并列拉索之間設(shè)置連接器。設(shè)置連接器后拉索面內(nèi)局部振動(dòng)頻率與拉索分段索長(zhǎng)成反比關(guān)系。以最長(zhǎng)索MC26為例,索長(zhǎng)288 m,在設(shè)置5個(gè)連接器后,拉索局部振動(dòng)頻率可以由0.7 Hz提高到4.2 Hz。在拉索系統(tǒng)阻尼比為0.5%的情況下,馳振發(fā)生風(fēng)速可以提高到45.5 m/s。由此可見(jiàn),通過(guò)設(shè)置連接器,可以提高局部振動(dòng)頻率,并可以達(dá)到提高尾流馳振發(fā)生風(fēng)速的目的。另外,設(shè)置連接器之后的并列拉索,也能夠起到限制拉索面外局部振動(dòng)的作用,由此也會(huì)對(duì)尾流馳振抑制發(fā)揮較好作用。
4 結(jié)論
本文通過(guò)對(duì)并列拉索靜氣動(dòng)力系數(shù)進(jìn)行了數(shù)值模擬,獲得了橫風(fēng)下并列拉索的靜風(fēng)荷載特征,并在馳振的判別原則的基礎(chǔ)之上開(kāi)展并列拉索尾流馳振的判別方法和發(fā)生風(fēng)速研究,并以中間索面斜拉橋?yàn)槔M(jìn)行了實(shí)例研究,研究表明:
(1)在橫風(fēng)作用下,并列拉索的上游索對(duì)下游拉索有明顯的阻擋效應(yīng),形成了下游拉索較低的阻力系數(shù)。
(2)下游拉索的升力系數(shù)在風(fēng)攻角較小時(shí)表現(xiàn)為先增加后減小的吸力,在較大風(fēng)攻角時(shí)表現(xiàn)為先增加后減小的斥力,同時(shí)升力系數(shù)具有較大的負(fù)斜率,馳振力系數(shù)最小為-3.356。
(3)下游拉索的尾流馳振分析表明,最長(zhǎng)拉索在阻尼比0.1%情況下的尾流馳振發(fā)生風(fēng)速很低,當(dāng)阻尼比提高到0.5%時(shí)馳振發(fā)生風(fēng)速仍為7.58 m/s,可見(jiàn),對(duì)于中間索面斜拉橋而言,拉索的尾流馳振問(wèn)題必須引起重視。
(4)在對(duì)增設(shè)連接器的并列拉索馳振風(fēng)速分析表明,增設(shè)連接器可以提高拉索的局部振動(dòng)頻率,從而達(dá)到提高尾流馳振發(fā)生風(fēng)速的目的,且尾流馳振發(fā)生風(fēng)速與拉索局部索長(zhǎng)成反比。
[1]陳政清.橋梁風(fēng)工程[M].北京:人民交通出版社,2005.
[2] Tanaka H.Aerodynamics ofcables. Fifth International Symposium on Cable Dynamics[C].Italy,2003:11-21.
[3]胡建華,趙躍宇,劉慕廣,等.串列雙索氣彈模型的風(fēng)洞試驗(yàn)研究[J].動(dòng)力學(xué)與控制學(xué)報(bào),2006,4(2):179-186.
HU Jian-hua,ZHAO Yao-yu,LIU Mu-guang,et al.Wind tunnel studies on the behavior of aeroelastic twin cable model[J].Journal of Dynamics and Control,2006,4(2):179-186.
[4]陳政清,劉慕廣,劉志文.基于氣彈模型的串列主纜氣動(dòng)干擾試驗(yàn)研究[J].振動(dòng)與沖擊,2008,27(8):7-11.
CHEN Zheng-qing, LIU Mu-guang, LIU Zhi-wen.Experiment study of aerodynamic interference of tandem cables based on aAeroelastic model[J].Journal of Vibration and Shock,2008,27(8):7-11.
[5]劉慕廣.兩類大長(zhǎng)細(xì)比橋梁構(gòu)件的風(fēng)振特性研究[D].長(zhǎng)沙:湖南大學(xué),2009.
[6] Desai Y M,Yu P,Popplewell N,et al.Finite element modelling of transmission line galloping[J].Computers &Structures,1995,57(3):407-420.
[7] Sockel H,Watzinger J.Vibrations of two circular cylinders due to wind-excited interference effects[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74-76:1029-1036.
[8]陳志華,李毅佳,王小盾.斜拉橋索的風(fēng)振現(xiàn)象及天津慈海斜拉橋的抑振措施[J].鋼結(jié)構(gòu),2007,22(1):65-69.
CHEN Zhi-hua,LI Yi-jia,WANG Xiao-dun.Wind-induced vibration for stay cables of cable-stayed bridges and vibration control method forcihaibridge oftianjin[J], Steel Construction,2007,22(1):65-69.
[9]李永樂(lè),王 濤,廖海黎.斜拉橋并列拉索尾流馳振風(fēng)洞試驗(yàn)研究[J].工程力學(xué),2010,(S1):216-221.
LI Yong-le,WANG Tao,LIAO Hai-li,Investigation on wake galloping of parallel cables in cable-stayed bridge by wind tunnel test[J].Engineering Mechanics,2010,(S1):216-221.
[10]陳艾榮,艾輝林,計(jì)算橋梁空氣動(dòng)力學(xué)-大渦模擬[M].北京:人民交通出版社,2010.

