數(shù)學教學中如何培養(yǎng)學生的學習興趣
目前,不少農(nóng)村的小學生不愛學習數(shù)學,對數(shù)學感到索然無味。究其原因,是他們?nèi)狈W習興趣。新課改強調(diào)以學生為中心,視其為學習的主人,注重把“學”“想”和“做”的機會多留給學生。托爾斯泰說過:“成功的教學所需要的不是強制,而是激發(fā)學生的興趣。”因此,讓學生對數(shù)學產(chǎn)生興趣,是提高學生數(shù)學能力的關(guān)鍵。那么,在數(shù)學教學課堂教學中如何激發(fā)學生的學習興趣呢?
一、新課導入,激發(fā)興趣
好的開頭是成功的一半。成功的導課能迅速集中學生的注意力,誘發(fā)學習興趣,激蕩他們急于學習的情感漣漪,為整堂課的高效教學打下堅實的學習基礎(chǔ)。如,我在教學年、月、日時,先出示一題激趣:小麗今年9歲,哥哥小光從出生到今年只過了3個生日。請同學們想一想,小光今年幾歲?話音剛落,一個學生順口答曰:“3歲。”全班哈哈大笑,對呀,妹妹今年都9歲了,哥哥怎么才3歲呢?班里開始議論紛紛,但誰都沒有說出正確答案。“不憤不啟,不悱不發(fā)。”在全班學生都渴望求得結(jié)果又很無奈時,我說:“學完這節(jié)課大家就會解答了,想學嗎?”同學們齊聲如洪:“想學!”如此導入,調(diào)動了學生學習的濃厚興趣和迫切探究新知的欲望。
二、創(chuàng)設(shè)問題情境,激發(fā)興趣
孔子說:“知之者不如好之者,好之者不如樂之者。”只有遵循兒童的年齡特點,從他們的實際水平出發(fā),在教學中相機激發(fā)學生的興趣,才會使學生全身心投入到學習的意境中。小學生大都溺愛游戲,提及游戲他們就樂不可支。根據(jù)這一特點,我在教學“能被2、5整除的數(shù)的特性”時,便選用游戲即興創(chuàng)設(shè)情境:“現(xiàn)在我們師生來比賽做一個數(shù)字游戲,看誰最聰明,能把老師考倒。你們隨意說出任何一個數(shù),我立即說出它能被2或5整除,或同時能被2和5整除。”學生們一聽,個個興致勃勃,爭先恐后地搶著說數(shù),有的還一心想難倒我,故意說出比較大的數(shù),結(jié)果我回答的居然又對又快。學生們無不為之驚嘆:老師為什么能準確流利地回答呢?莫非有什么絕招不成?就這樣他們懷揣好奇,帶著疑問和追求新知的欲望,快速地跨入了探究新知的殿堂。
三、引領(lǐng)動手操作,激發(fā)興趣
著名心理學家皮亞杰說:“兒童的思維是從動作開始時,切斷動作與思維的聯(lián)系,思維就不能得到發(fā)展。”可見,動作性的活動,能促進兒童理解學習中的疑難,并在理解中發(fā)展思維,通過具體操作,學會新知。在數(shù)學教學中,必要時不妨引領(lǐng)學生進行動手操作,讓他們手、口、眼、腦協(xié)調(diào)活動,他們就會全身心地投入,思維得以激活,使學習成為一種活躍身心、和諧器官的運動,益于快速地變抽象為直觀,通過親自“躍一躍”,即刻達成摘到“桃子”的功效。如,在教學幾何圖形時,教師就應引導學生先通過拼拼、擺擺、量量、折折、剪剪,再相機啟發(fā)他們在一些必要的環(huán)節(jié)看看、想想、說說、畫畫、議議,問題往往就能迎刃而解。如,在教學“環(huán)形面積的計算”時,由于大部分學生對環(huán)形接觸的較少,他們一時不知從何下手,如果直接告訴他們計算的方法,勢必沖淡了他們的主體作用。“授之以魚不如授之以漁。”于是,我從舊知著眼,引領(lǐng)學生自己動手,先剪下一個半徑9厘米的圓,并計算其面積;再在剪下的圓上任意畫一個半徑小于9厘米的同心圓,自己剪下并快速計算出這個小圓的面積。兩次剪圓后,一個剩下的環(huán)形就立刻映入學生的眼簾。至此,什么是環(huán)形,學生就輕松地理解了。不僅如此,絕大多數(shù)學生通過實際操作,很快算出了環(huán)形的面積,并由此非常直觀地地推導出環(huán)形面積的公式。如此引領(lǐng),學生在動手的過程中既掌握了新知,學會了公式推導的途徑,又徜徉在學習數(shù)學的樂趣之中,不再感到數(shù)學枯燥、單一和無味。
四、巧設(shè)開放題,激發(fā)興趣
教師要打破教材的約束,一味地為教材而教教材,必要時,要設(shè)計一些數(shù)學開放題,引領(lǐng)學生予以求解。誠然,開放題既沒有現(xiàn)成的答案,也沒有現(xiàn)成的教法,操作起來有一定難度,不少學生也會知難而退。教育家夸美紐斯說:“應該用一切可能的方式把孩子們的求知欲與求學的欲望激發(fā)起來。”因此,教師要注重巧妙激發(fā)學生的求知“欲”和求學“欲”,提升學習的效率。
如,一次教學展示課,我執(zhí)教完“三角形面積計算”之后,我借助多媒體出示了如下一道開放題:
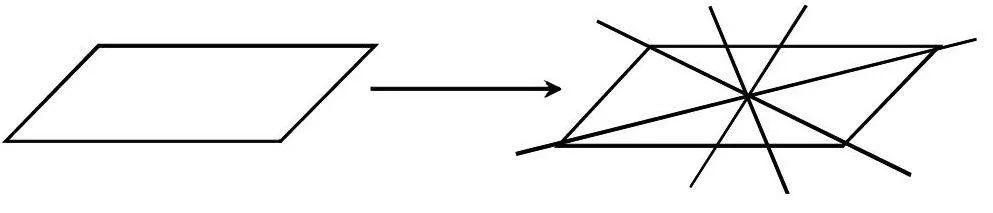
在下圖平行四邊形中畫上一條直線,把平行四邊形分成兩個面積完全相等的圖形,誰畫的最多,誰就是“智慧星”。
聽說要評“智慧星”,學生樂了,忙不迭地地操作起來。但我巡視時發(fā)現(xiàn),絕大多數(shù)學生畫的往往都是對角線,他們僅僅把平行四邊形分成兩個相等的三角形,當然,這種畫法對本課三角形面積計算的推導得到進一步的鞏固和認識。但如果就此停止,就喪失了一次開發(fā)創(chuàng)新思維的佳機。于是,我首先肯定了這些學生的成績,然后予以啟發(fā):“其實,不止兩條對角線,還能畫很多條直線呢,我看那些同學最聰明,畫好后不妨對折一下,如果兩部分完全重疊了,說明你離‘智慧星’就不遠了。”果不其然,不少學生通過兩條對角線的交點畫出了很多條直線。
(作者單位 江蘇省新沂市合溝鎮(zhèn)中心小學)
編輯 劉青梅

