針對數學教師的范希爾幾何思維水平測試

官紅嚴，周 超

（蘇州大學 數學科學學院，江蘇 蘇州 215006）

針對數學教師的范希爾幾何思維水平測試

官紅嚴，周 超

（蘇州大學 數學科學學院，江蘇 蘇州 215006）

世界范圍內對學生幾何思維水平關注的很多，然而對老師的關注卻很少．利用Usiskin的測試卷測試了137位在職數學教師的范希爾幾何思維水平，結果顯示大多數老師都在水平4及以上，有27%的老師在水平5．這樣的結果與中國長期的高水平的幾何教學有關．

范希爾理論；數學教師；幾何思維水平

20世紀50年代，荷蘭學者范希爾（Van Hiele）夫婦把幾何思維劃分為5個水平[1]：

水平1：直觀（visuality）．學生能按照外觀從整體上區分幾何圖形，他們對圖形的區分往往依賴于具體樣板．

水平2：分析（analysis）．學生已經能夠認識圖形的特征性質，并依據性質做圖形分類．

水平3：非形式化的演繹（informal deduction）．這時學生已能形成抽象的定義，區分概念的必要條件和充分條件，并能通過非形式化推理將圖形分類．

水平4：形式的演繹（formal deduction）．學生可以了解到證明的重要性和了解“不定義元素”、“公理”的意義，理解幾何學中的公理、定義、定理等，也能推理出新的定理，建立定理間的關系網絡．

水平5：嚴密性（rigior）．學生能在不同的公理系統下嚴謹地建立定理，以分析比較不同的幾何系統，如歐式幾何與非歐幾何系統的比較．

這一理論很快引起了國際數學教育界的普遍關注，相關的研究包括以下幾個方面：一是進一步證實范希爾水平的合理性；二是編制范希爾水平測試卷，考察不同年級學生的范希爾幾何思維水平；三是依據范希爾水平構建幾何課程體系；四是考察范希爾水平與其它認知因素的相關性．在上述研究中，范希爾幾何思維水平的測量是一項基礎研究，但以往的研究主要是考察學生的范希爾幾何思維水平，針對數學教師的相關研究極少．

文章的目的是考察中國在職數學教師的范希爾幾何思維水平．根據范希爾理論的特點，學生的幾何思維水平不是自然增長的，需要通過適當的教學來提升．很多研究教師專業發展的學者也認為[2~3]，教師的知識深度和廣度對幫助學生學習數學至關重要．因此，教師的幾何思維水平對學生的幾何學習有重要的影響．

1 教師幾何思維水平的相關研究

范希爾幾何思維水平的調查絕大多數是針對學生的，涉及教師的不多．其中，Mayberry（1983）[4]是第一個從事這方面研究的人．她前后訪談了19位師范生．研究表明，大多數學生都缺乏學習形式演繹幾何課程的準備知識．這一結果后來被多人證實．Lawrie and Pegg[5]（1997）根據Mayberry的訪談提綱設計了一套書面測試卷，對60名師范生進行了測試，結果表明，大多數師范生的思維水平都只達到了水平1和水平2．

Lin，Cheng-Yao[6]等人利用測試卷對48名美國和40名臺灣的職前小學教師的研究表明，臺灣的職前小學教師的范希爾幾何思維水平明顯高于他們的美國同行們．Erdogan Halat[7]對土耳其的125名職前小學教師和156名職前中學教師進行了測試，結果表明兩類教師在幾何推理階段并沒有顯著差異，另外雖然職前中學男教師的范希爾幾何思維水平好于女教師，但是在職前小學教師中并沒有發現性別差異．

2 研究方法和數據分析

2.1 研究對象

研究的施測對象是在蘇州大學攻讀教育碩士學位的2006及2007級成員，共施測139人，其中有兩人沒有完成試卷．故這里只對余下的137名樣本進行分析．137名對象均是來自蘇南地區的在職數學教師，其中1名來自小學，19名來自職業學校，其他來自普通中學．其中男教師32名，女教師105名．

2.2 研究工具

在范希爾幾何思維水平的研究中，最經典的是美國芝加哥大學尤西斯金（Usiskin）的工作．他主持了一項包括了6個州的學習高中幾何課程的近2900名學生的題為“中學幾何課上學生認知發展和成就”的研究課題，這項研究的目的是確定學生的認知發展階段以及學生在數學基礎知識測驗上的成績對他們掌握幾何概念和證明的影響．在這項研究中包含了4個測驗，其中包含一個范希爾幾何水平的測試卷[8]．該測試卷直到今天仍被許多人引用．研究者在征得Usiskin本人的同意后，將這套測試卷翻譯成中文，作為這一項目的研究工具．

2.3 計分標準

Usiskin的范希爾測試卷共25題，均為有5個選項的選擇題．從低到高，依次每5題歸屬于一個水平．計分標準采用文[8]中的一種計分標準：每個水平的題目答對4題及以上分別記為1、2、4、8、16分，答對4題以下不計分．然后合計總分．這樣計分的好處是對任何在0—31的數字都可以判斷出在5個水平的得分情況．理想的假設是一位被試被認為處在Van Hiele水平n，如果他不僅水平n的題目得分而且水平n之前的所有水平的題目都得分，因此，若總分是1分，記其Van Hiele水平為水平1；總分為3分，記為水平2；總分為7分，記為水平3；總分為15分，記為水平4；總分為31分，記為水平5．

3 測試結果分析

依照上述計分標準，137份樣本中有29份是不能判斷處于哪個水平的，在其余108人中除有1人是水平2之外，其余均在水平3至水平5，具體見表1．

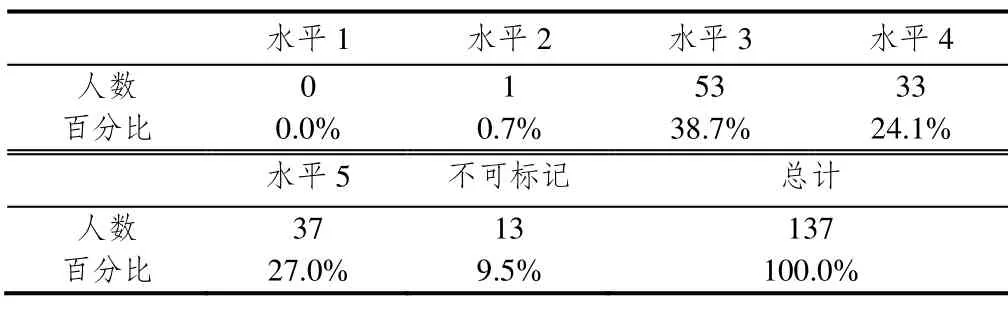
表1 答對4題及以上計分標準下的統計結果

從表1可以看出，在所有被試中53人，即38.7%被試處在水平3，五分之一強的人達到水平4，多于四分之一的教師可以達到最高水平．值得注意的是，19名職業學校老師中，有5名不能判斷處于哪個水平，11名在水平4之下．這表明在樣本中，職業老師的幾何思維水平比普通中學老師略低．

下面具體看看測試卷中的題目及被試教師們在這些題目上的表現（見圖1）．

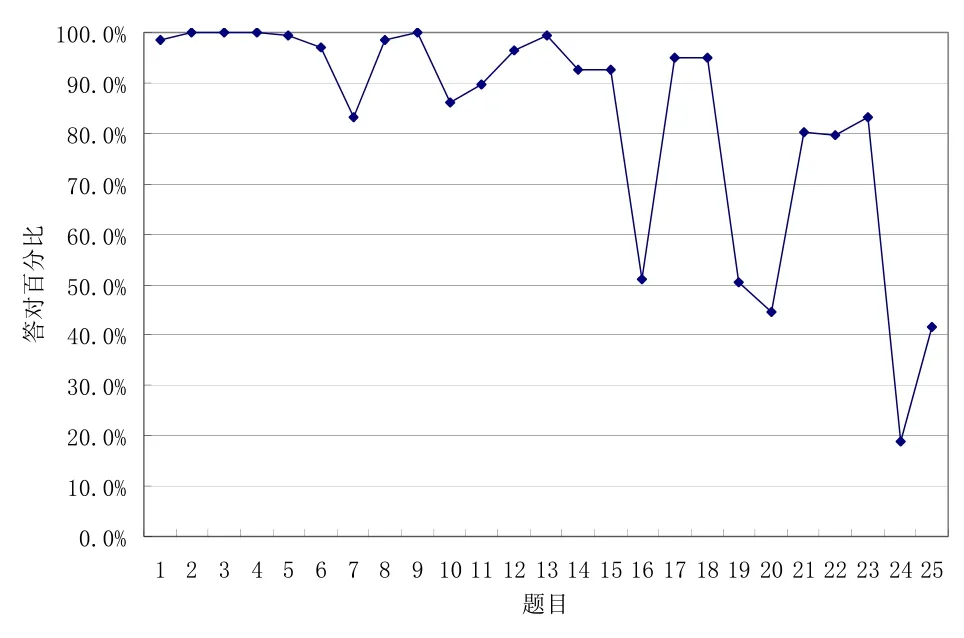
圖1 各題答對率

從圖1可知前3個水平的題目答對率都在80%以上，教師在第16、19、20、24和25題的答對率是均低于50%．

第16題：有一個直角三角形ABC，在它的每條邊上都構造一個等邊三角形ACE，ABF和BCD（如圖2）．根據上述條件，可以證明AD，BE，CF交于一點．從這個證明中，你可以肯定的是：

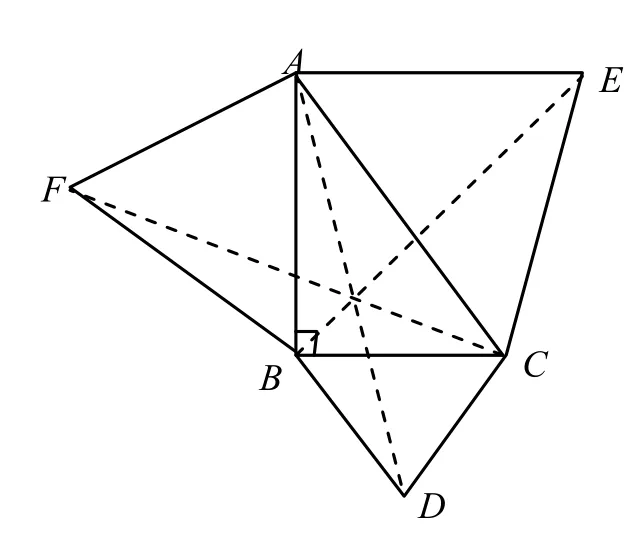
圖2 第16題

（A）只有在所給的圖形中，AD、BE、CF才交于一點；

（B）對于有些直角三角形，但不是全部，AD、BE、CF交于一點；

（C）對于任意直角三角形，AD、BE、CF交于一點；

（D）對于任意三角形，AD、BE、CF交于一點；

（E）對于任意等邊三角形，AD、BE、CF交于一點．

正確答案是對所有的直角三角形AD、BE、CF交于一點．這道題目涉及證明，要回答好這題必須理解證明的意義，所以這是一道水平4的題目．近一半的人選擇了錯誤的答案．周超等[9]對教師證明素養的調查顯示中國數學教師數學證明的基本功還是很扎實的．教師選擇錯誤的原因或許是題目給出的結論確實是在任意三角形中都可以成立的結論，而在所有的錯誤答案中選擇在任意三角形中都成立的教師也是最多的．

第19題有關幾何中的概念和命題：在幾何中，下列說法正確的是：

（A）所有概念都可以定義，所有真命題都可以證明；

（B）所有概念都可以定義，但必須假設某些命題是正確的；

（C）有些概念可以沒有定義，但所有真命題都可以證明；

（D）有些概念不可以定義，并且必須假設某些命題是正確的；

（E）以上都不對．

關于這個問題的正確選擇應該是：有些概念不可以定義，但必須假設某些命題是正確的．這也是水平4的題目，用來測量教師對定義和公理的理解．幾何的大廈是在幾個不可定義的概念和幾個不可證明的公理通過邏輯的演繹建立起來的，初高中的數學課本在引入平面和立體幾何時也是從不定義的概念和不證明的公理出發的，事實上只有半數多一點的人選擇了正確答案．

第24題是所有測試題中答對率最低的，僅為19.0%．題目是這樣的，有兩本書上對矩形的定義是不同的．你認為下列說法正確的是：

（A）有一本出現了差錯；

（B）其中有一個定義是錯誤的，矩形不可能有兩個不同的定義；

（C）其中一本書上的矩形與其它書上的矩形肯定有不同的性質；

（D）其中一本上的矩形與其它書上的矩形肯定有相同的性質；

（E）這兩本書上的矩形肯定有不一樣的性質．

這是一道涉及非歐幾何的題目，屬于水平5的題目，正確答案為E．在幾何體系中除了歐氏幾何之外還有多種非歐幾何，它們是依據不同于歐氏幾何的公理而來的．教師在第24題的作答，反應了很少教師了解這一事實，他們更多的是從歐氏幾何體系內部去考慮問題．這或許和中學教師在日常的教學中所面對的都是歐氏幾何有關，另一方面是否他們在高等教育階段在這部分所受的教育也不多呢？

4 結果與討論

上述結果表明在職數學教師的幾何思維水平還是比較高的，然而也應看到并不是每個人都達到了形式演繹的水平．另一方面，教師對于幾何公理體系的建立過程和非歐幾何是不大了解的．這可能跟教師日常處理的教學有關．此外，研究數據顯示，職業學校老師的幾何思維水平大多在水平3．由于考試升學的壓力，教師教學過程中要處理大量的練習題，許多學校也是根據學生的考試成績來評定教師的教學水平，導致教師在自己的教學過程中也是把解數學題放到了首位，這樣做的結果可能是教師也忽視了對自己思維水平的要求．然而，作為一名數學教師不僅需要數學知識和一般的教學法知識，還需要知道關于某一數學內容該如何組織和呈現、學生是怎樣學習這一數學內容的、可能會遇到什么困難等方面的知識[10]．因此，在相關的師范教育和教師培訓中應該對教師的幾何思維水平提出更高的要求，這樣在他們的教學中才有可能對學生提出更高的要求，有利于學生形成良好的數學思維．

限于樣本的原因，在研究中沒有發現男女教師反應上的差異，這是一個值得繼續探討的問題．此外研究只是選取了蘇南地區的一百多位教師進行測試，還需要使用更大范圍的樣本進行更深入的分析．另外，研究中采用的測試卷是Usiskin等人編制用來測試學生的范希爾幾何思維水平的，用來測試老師也可能產生一定的偏差，編制專門針對教師的測試卷也是一個值得繼續探討的問題．

[1] 鮑建生，周超．數學學習的心理基礎與過程[M]．上海：上海教育出版社，2009．

[2] 王子興．論數學教師專業化的內涵[J]．數學教育學報，2002，11（4）：63-67．

[3] 于曉娟，王家鏵，李忠海．發展數學教師知識結構的若干策略[J]．數學教育學報，2006，15（2）：32-34．

[4] Mayberry. The Van Hiele Levels of Geometric Thought in Undergraduate Preservice Teachers [J]. Journal for Research in Mathematics Education, 1983, (14): 58-69.

[5] Lawirie C, Pegg J. Some Issues in Using Mayberry’s Test to Identify van Hiele Levels [C]. Proceedings of the 21st Conference of the International Group for Psychology of Mathematics Education, Lahti, 1997.

[6] Cheng-Yao L, Fenqjen L, Jane-Jane L, et al. U.S. and Taiwanese Pre-Service Teachers’ Geometry Knowledge and Thinking [J]. International Journal for Mathematics Teaching and Learning, 2011, (10): 1-29.

[7] Halat E. Pre-Service Elementary School and Secondary Mathematics Teachers’ Van Hiele Levels and Gender Differences [J]. Issues in the Undergraduate Mathematics Preparation of School Teachers, 2008, (5): 1-11.

[8] Usiskin Z. Van Hiele Levels and Achievement in Secondary School Geometry [Z]. (Final Report of the Cognitive Development and Achievement in Secondary School Geometry Project). Chicago: University of Chicago, (ERIC Reproduction Service No. ED220288), 1982.

[9] 周超，鮑建生．對中學數學教師證明素養的一次調查[J]．數學教育學報，2009，18（6）：42-44．

[10] 童莉．數學教師專業發展的新視角——數學教學內容知識（MPCK）[J]．數學教育學報，2010，19（2）：23-27．

Survey on Van Hiele Geometric Thinking Levels of Chinese Mathematics Teachers

GUAN Hong-yan, ZHOU Chao
(School of Mathematical Sciences, University Suzhou, Jiangsu Suzhou 215006, China)

There are many studies focus on students’ van Hiele geometric thinking levels, few on mathematics teachers. This paper investigated van Hiele geometric thinking levels of 137 Chinese mathematics teachers via the test designed by Usiskin*. The finding shows that the majority of sample teachers are on level 4, and there are 27 percent of sample teachers are on level 5. The result is partly due to the high level geometry teaching of China for a long time. (*the authors translate the test of Usiskin into Chinese under the permission of Zalman Usiskin)

van Hiele theory; Chinese mathematics teachers; geometric thinking levels

G420

：A

：1004–9894（2014）02–0083–03

[責任編校：周學智]

2013–11–10

官紅嚴（1988—），女，江蘇徐州人，碩士研究生，主要從事數學教育研究．本文通訊作者周超．