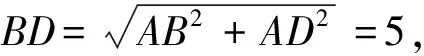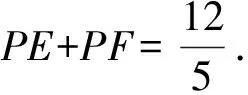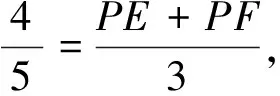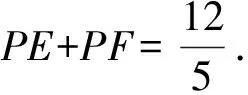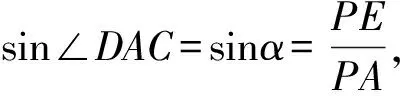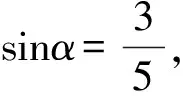“微探究”為數學課堂教學增色
江蘇省張家港市第一中學 (郵編:215600)
“微探究”是根據教學內容,圍繞某個小知識點或某一問題,在教師的組織、引導下,讓學生用自我探究或合作交流的方式學習.在10年的課改過程中,探究教學的理念雖然已經深得人心,探究式教學的方式已經在數學教育界形成了廣泛的共識.但真正做到在課堂教學中的常態化卻舉步為艱,教學的現狀令人擔憂.而微型探究教學作為探究教學的一種,為數學課堂探究教學找到了一種有效的實施途徑.筆者結合教學實踐,就數學課堂教學各環節中如何滲透微探究,淺談自身的做法與體會,供參考.
1 概念中的微探究,讓學生發現概念的形成過程
教學片斷1 在蘇科版數學七年級上冊“2.7有理數的乘方”的教學中.
師:你還記得嗎?若正方形的邊長為a,則正方形的面積是?
生:a2.
師:若一個正方體的棱長為a,正方體體積是?
生:a3.
師:“做一做”,將一張報紙依次對折1次,2次,3次,4次,5次,…,觀察報紙發生了什么變化?
生1:報紙越來越小.
生2:報紙越來越厚.
師:觀察對折的次數與報紙的層數之間有什么關系呢?
生:交流發現
對折次數 層數
1次 2
2次 2×2
3次 2×2×2
4次 2×2×2×2
5次 2×2×2×2×2
… …
師:對折10次呢?
生:10個2相乘.
師:對折100次呢?
生:100個2相乘.
師:很好,但這樣表示的話會不會給我們的寫法上帶來不便呢?
生:可以用省略號表示.
師:就算用省略號表示也還是有些復雜,有沒有更好的辦法呢?
生:(沉默)
師:想想a2表示2個a相乘,想想a3表示3個a相乘.
生:知道了!
學生總結乘方的記法和讀法
層數 記作 讀作
2×2 =222的平方(2的2次方)
2×2×2 =232的立方(2的3次方)
2×2×2×2 =242的4次方
2×2×2×2×2 =252的5次方
… …
乘方的定義:求相同因數積的運算,叫做乘方.乘方的結果叫做冪.
設計意圖讓學生動手操作后觀察發生了哪些變化,學生可能從報紙的厚度、大小、報紙的層數等方面發現了其中的變化,引導學生進一步觀察對折的次數與報紙的層數之間所發生的變化,發現折次數和層數之間的關系?學生交流發現后很容易就發現規律,但當相同的因數過多后,會感覺到用算式表達太復雜,迫切需要一種簡單的表示方法.這種方法就是乘方,充分體現了引入乘方這個概念的自覺性和必要性. 通過回憶小學里學習過平方和立方的知識進行類比,猜想4次方、5次方等表示方法.同時由特殊的數字2引申到a,讓學生體會從特殊到一般的思想.另外通過讀法能夠讓學生明白乘方的意義,同時切身感受到為什么要引入乘方的表示方法,目的是書寫的方便. 通過整個引入過程中的微探究,學生發現了乘方這個概念的形成過程,掌握了概念的本質.
2 知識點中的微探究,讓學生感受知識的發生、發展過程
教學片斷2 在蘇科版數學九年級上冊“5.5直線與圓的位置關系”的教學中.
師:看圖判斷下列直線和圓的位置關系?
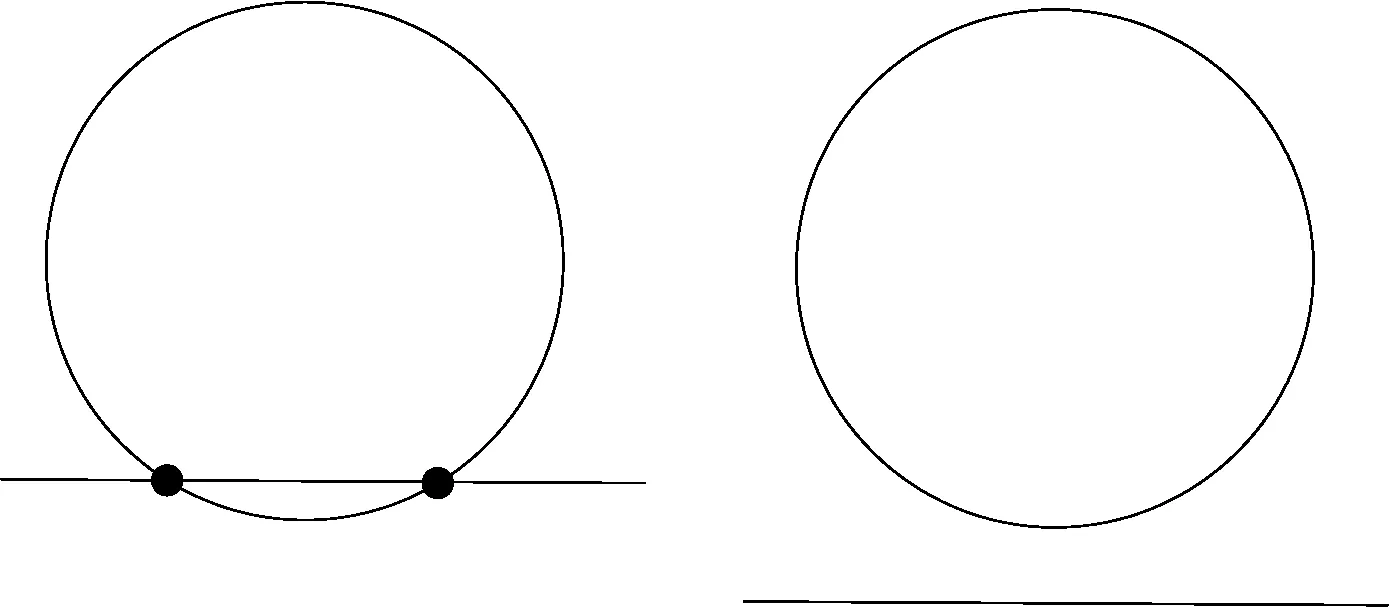
(1) (2)

(3) (4)
生1:(1)相交
師:理由是什么?
生1:直線與圓有兩個公共點.
生2:(2)相離,沒有公共點.
生3:(3)相切,只有一個公共點.
生4:(4)相切,有一個公共點.
生5:(4)好像不是一個公共點.
師:那到底是什么位置關系呢?如果公共點個數不好判斷,該怎么辦?
生:(沉默)
師:點和圓的位置關系有幾種?如何判斷點和圓的位置關系?
生:3種,在圓外,在圓上,在圓內.
生:根據點到圓心的距離d和半徑r的大小來比較.
d>r?在圓外;
d=r?在圓上;
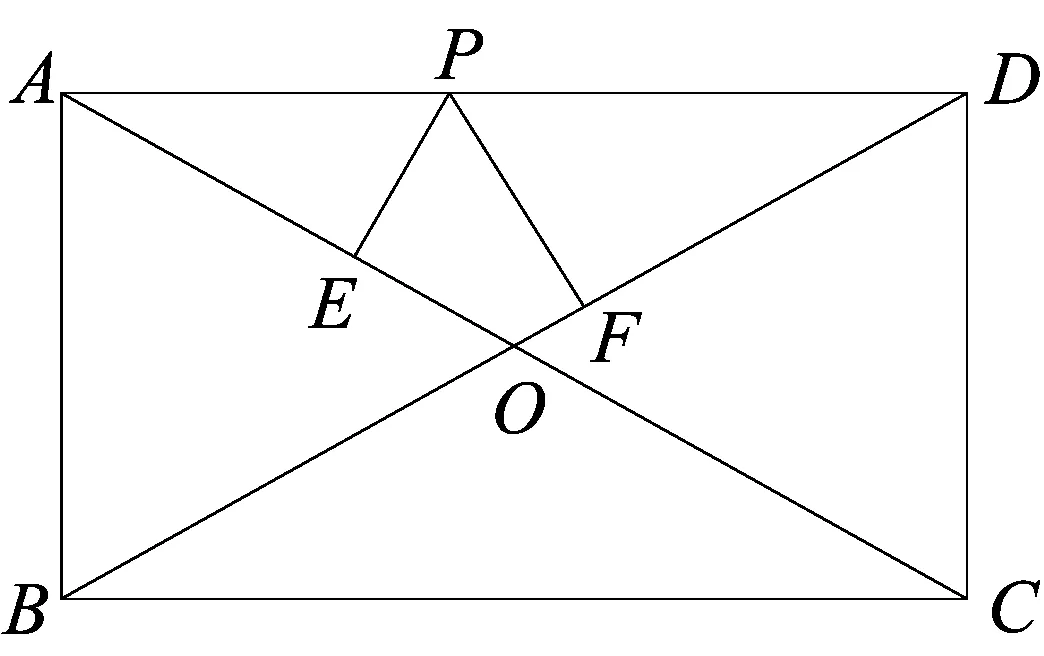
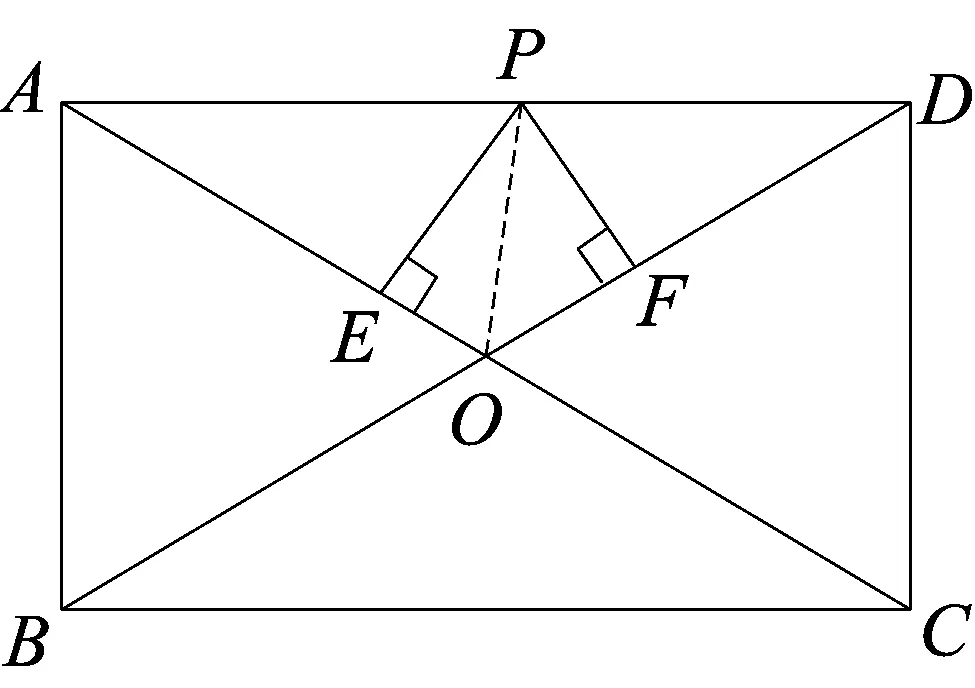
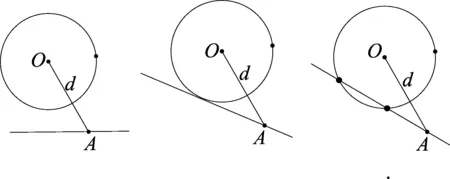
d 師:“直線和圓的位置關系”能否像“點和圓的位置關系”一樣用數量關系來表示呢? 師:下面把點A變成一條直線,過點A任意作一條直線(如圖1),能否用OA的長與半徑r來比較確定直線與圓的位置關系呢? 圖1 圖2 圖3 生:不能. 師:請看圖2,圖3,此時OA的長沒有變,但直線與圓的位置關系已經變了,確實不行. 師:看來用OA這條線段的長和半徑r比較不能確定直線與圓的位置關系,因為此時直線可以繞著點A變化.那有沒有其它可以的呢? 生:作垂線段. 師:怎么作垂線段? 生:過圓心作直線的垂線段. 師:此時可以嗎,為什么? 生:過直線外一點只能作一條垂線段,此時它不會再繞著點D變化了. 師:那么判斷直線與圓的位置關系需要找到哪條線段呢? 生:找圓心到直線的垂線段,用垂線段和半徑r比較. 設計意圖本節知識的難點在于找到圓心到直線的距離,通過圓心與直線的距離和半徑比較來從數量上判斷直線與圓的位置關系.首先通過復習點與圓的位置關系,在點與圓的位置關系的基礎上,把點變為直線后,進行類比探索直線與圓的位置關系.同時通過探究發現,直線上任意一點和圓心的線段和半徑比較不能反映直線與圓的位置關系,只有圓心到直線的垂線段的長和半徑比較才能確定直線與圓的位置關系.讓學生進一步體會到:直線與圓的位置關系可以轉化為點到直線的距離和半徑之間的數量關系;反過來,也可以通過點到直線的距離與半徑之間的數量關系判定直線與圓的位置關系. 整個過程通過微探究讓學生由點變線,由普通線段到垂線段,感受知識的發生、發展的過程,弄清知識的來龍去脈,形成完整的知識體系. 教學片斷3 在蘇科版數學八年級下冊“11.2反比例函數”的教學中. 在學生進行代入法和圖象法兩種方法解決問題后,設計以下問題: 設計意圖在例題的教學中,利用微探究可以使學生理解問題的本質,便于學生實現真正意義上的自我建構.問題1是在例題的基礎上把反比例函數的解析式進行了變化,學生采用圖象法馬上可以解決.這時要引導學生采用代入法進行完成,由于系數k的不確定,有的學生可能無從下手,有的學生會想到取特殊值進行處理,培養了用創造性思維去解決問題. 問題2是在問題1的基礎上把幾個點的坐標也變成了未知數,這時學生在問題中學會了用特殊值法解決,從而更好的鞏固了這類例題.問題3和問題4是在問題1、2的基礎上繼續強化學生對這兩種方法的掌握,使學生的思維更加深刻,更好的理解幾個問題之間的邏輯關系,真正提高了分析問題、解決問題的能力. 數學例題的教學,一直是課堂教學的一個關鍵,通過微探究進行教學,主要是讓學生帶著問題進行學習,通過自身的積極探索,由表及里,由簡入難的掌握知識,從而真正實現了知識的自我建構. 教學片斷42013年濟寧市中考數學三模14題. 如圖,在矩形ABCD中,AB=3,AD=4,P是AD上一動點,PE⊥AC于E,PF⊥BD于F,則PE+PF=________________. 分析由題意PE、PF是高,由高可以聯想到三角形的面積,連接PO,則PE、PF是△OAP和△ODP的高,通過等積法可以完成. 解法一在直角△ABD中,AB=3,AD=4, 所以OA=OD=2.5, 即△ODP的面積+△OAP的面積=3, 2.5(PE+PF)=3, 思考解法一是根據面積相等來完成的,還有其它的方法嗎? 分析由題意PE、PF是高,可以發現△AEP∽△ADC,△DFP∽△DAB,這樣利用相似可以解決嗎?學生探究. 解法二設AP=x,PD=4-x. 因為∠EAP=∠EAP,∠AEP=∠ADC, 所以△AEP∽△ADC,故 ① 同理可得△DFP∽△DAB,故 ② 思考解法一是根據面積相等來完成的,解法二是利用相似來完成的,還有其它的方法嗎? 分析由題意PE、PF是高,可以發現△PAE、△PDF都是直角三角形,由直角三角形就會想到三角函數,那么利用三角函數能解決嗎?學生探究. 解法三因為四邊形ABCD是矩形,AB=3,AD=4, 所以BD=AC=5,OD=OC,所以設∠BDC=∠DCA=α, 所以PE=PAsinα, 所以PE+PF=PAsinα+PDsinα=ADsinα, 因為在Rt△BAD中,AB=3,AD=4,BD=AC=5, 設計意圖在習題的教學中,利用微探究可以使學生思路不斷拓寬,思維更加發散.解法一是根據PE、PF是高,由此聯想到三角形的面積,利用等積法來解決的.解法二在此基礎上繼續探究,發現PE、PF是高可以得到兩對三角形相似,那利用相似能否解決問題呢,學生在探索后發現也可以解決.解法三是發現PE、PF是高后,存在兩個直角三角形,由直角三角形想到三角函數,學生經過探究后發現利用三角函數的知識也可以解決.本道習題在解法一完成的基礎上并沒有結束,而是讓學生進一步去探索,在探索的過程中思路不斷的拓寬,采用不同的思想都可以解決. 學生通過對這三種方法的掌握,使學生的發散思維和創新思維得到了進一步發展. 微探究可以運用在數學課堂的各個環節,運用微探究組織教學活動時,結合具體的教學內容,可以改變單一的教學方式,培養學生的探索意識和創新能力.讓學生在概念教學中感受到概念的形成過程,在知識點的掌握中體會知識的發生、發展過程,在例題的學習中理解知識的本質,真正實現自我建構,在習題的訓練中不斷拓寬思路,進一步培養學生的發散思維和創新能力,使數學的課堂教學煥發新的活力.

3 例題中的微探究,讓學生理解知識的本質,實現真正意義的自我建構


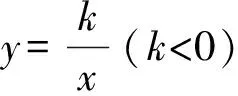
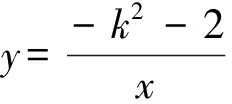
4 習題中的微探究,讓學生的思路不斷拓寬,培養發散思維和創新思維