實(shí)驗(yàn)探究一道中考平面幾何題的題源

安徽省歙縣中學(xué) (郵編：245200)

1 問題展示

問題如圖1，正六邊形ABCDEF的邊長為a，P是邊BC上一動點(diǎn)，過P作PM∥AB交AF于點(diǎn)M，作PN∥CD交DE于點(diǎn)N，

(1)①∠MPN=________°；

②求證：PM+PN=3a；

(2)如圖2，點(diǎn)O為線段AD的中點(diǎn)，連接OM、ON，求證：OM=ON；

(3)如圖3，點(diǎn)O為線段AD的中點(diǎn)，OG平分∠MON，判斷四邊形OMGN是否為特殊的四邊形，并說明理由．

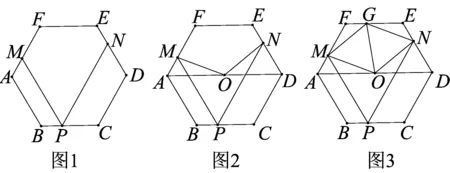
這是2014年安徽省初中畢業(yè)學(xué)業(yè)考試數(shù)學(xué)試題．其中“PM+PN=3a”的題源是非常明顯的：將正六邊形還原成為正三角形，就可發(fā)現(xiàn)“PM+PN為定值(邊長)”就是等腰三角形的性質(zhì)：過等腰△ABC底邊BC上任意一點(diǎn)P作兩腰的平行線，與兩腰分別相交于M、N兩點(diǎn)，則PM+PN為定值(腰長)．

在各類中考試題中，還經(jīng)常用到下列題源：

(ⅰ)若點(diǎn)P在等腰△ABC底邊BC兩端的延長線上，則|PM-PN|為定值(腰長)；

(ⅱ)等腰△ABC底邊BC所在直線上任意一點(diǎn)P到兩腰的距離之和(或差)為定值(腰上的高)．

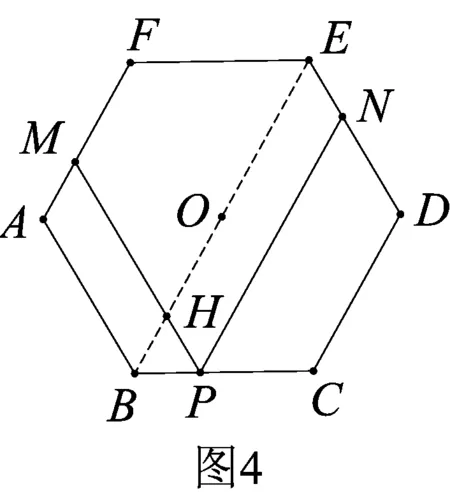
為了方便后續(xù)探究，下面僅給出一種證明方法：如圖4，連接BE交PM于H點(diǎn)，在正六邊形ABCDEF中，PN∥CD,又BE∥CD∥AF，所以BE∥PN∥AF.

又PM∥AB，所以四邊形AMHB、四邊形HENP均為平行四邊形，△BPH為等邊三角形.

故PM+PN=MH+HP+PN=AB+BH+HE=AB+BE=3a.

事實(shí)上，原中考題(2)是(3)(判斷四邊形OMGN是否為菱形)的一個(gè)步驟，因此，下面重點(diǎn)實(shí)驗(yàn)探究問題(3)的真正源頭在哪里？

2 實(shí)驗(yàn)探究△PMN“心” 的性質(zhì)

在《幾何畫板》中，通過實(shí)驗(yàn)容易發(fā)現(xiàn)△PMN的下列“心”的性質(zhì)：

性質(zhì)1△PMN的外心為定點(diǎn)(正六邊形的中心O),且∠MON=120°.

證明如圖2，由于正六邊形ABCDEF的邊AB、CD的中垂線交點(diǎn)就是該正六邊形的中心O，又由于等腰梯形上下兩底的中垂線重合，所以PM、PN的中垂線的交點(diǎn)也是O點(diǎn)，即△PMN的外心為O點(diǎn)．

由于∠MPN=60°，由(1)可知∠MON=2∠MPN=120°(同弧所對的圓心角是圓周角的兩倍)；

原考題第(2)小題正是這條性質(zhì)．

性質(zhì)2△PMN的重心G1始終在定直線AD上(如圖5).

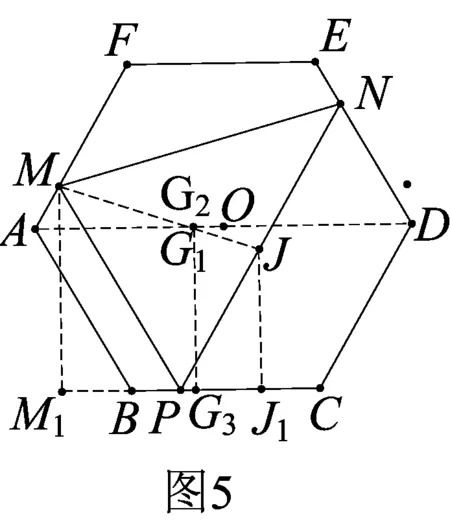
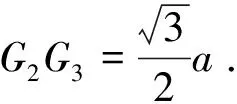
由三角形相似知識可得G2G3=

故G1與G2重合且在AD上.

性質(zhì)3△PMN的垂心始終在定直線AD上.

證明由于任意三角形的外心、重心、垂心共線(即所謂的歐拉線)，所以△PMN的垂心一定在直線AD上．

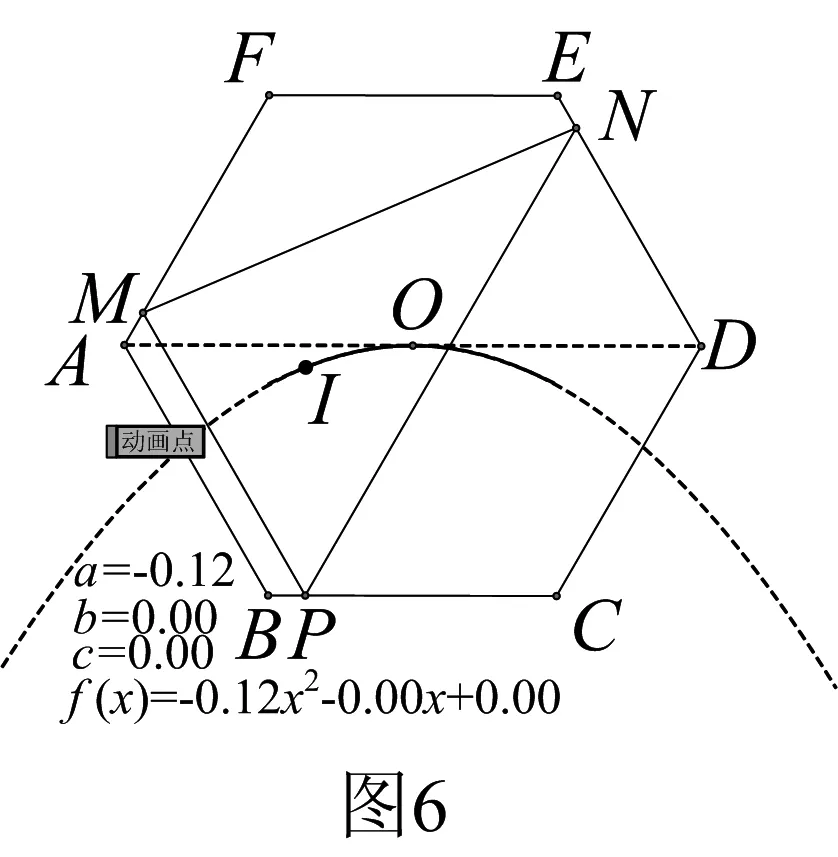
性質(zhì)4△PMN的內(nèi)心在某定二次函數(shù)上移動(如圖6).

(由于證明過程會用到高中知識，限于篇幅，這里僅給出實(shí)驗(yàn)結(jié)果圖)

3 實(shí)驗(yàn)探究△OMN“心” 的性質(zhì)

同上，通過數(shù)學(xué)實(shí)驗(yàn)容易發(fā)現(xiàn)△OMN的下列“心”性質(zhì)(如圖7)：

性質(zhì)1△OMN的外心的軌跡就是線段EF.

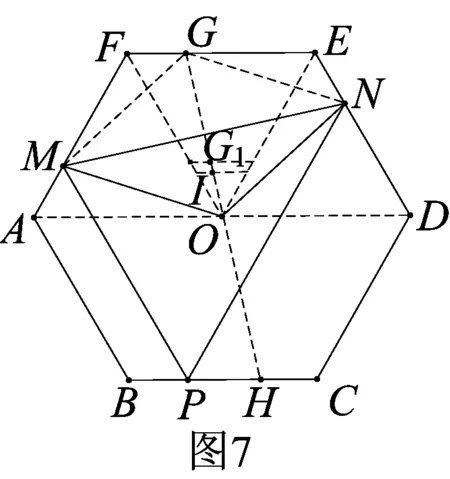
性質(zhì)2△OMN的垂心H的軌跡就是線段BC.

性質(zhì)3△OMN的重心G1始終在平行于AD的定直線上.

性質(zhì)4△OMN的內(nèi)心I始終在平行于AD的定直線上.

性質(zhì)5△OMN的外心、內(nèi)心、重心、垂心在過O點(diǎn)的同一直線上.

先證性質(zhì)1在圖7中，設(shè)MN的中垂線與EF相交于點(diǎn)G．則只要證GM=GN=GO；由于OG垂直平分

則只要證：OM=OG；

連接OE、OF，由∠AOF=∠MOG=60°可得∠AOM=∠FOG，因此△AOM?△FOG(ASA)，所以O(shè)M=OG．

從上述證明可得，若OG平分∠MON，則四邊形OMGN為菱形．

這正是原中考試題的第(3)小題所要證明的結(jié)論．

再證性質(zhì)2在圖7中，設(shè)MN的中垂線與BC邊相交于點(diǎn)H．連接HM、HN，要證H為△MON的垂心，只要證：△HMN為正三角形．

因?yàn)镺P=OM=ON=OG(已證)，又由正六邊形的對稱性可得OH=OG，

所以P、M、G、N、H五點(diǎn)都在以O(shè)為圓心的圓上．

又因∠MPN=60°,故∠MHN=60°，

又HM=HN，故△HMN為正三角形．

性質(zhì)3、4的證明與△PMN“心”的性質(zhì)2的證明類似，限于篇幅，具體過程這里略去．

證明性質(zhì)5因?yàn)椤鱉ON為等腰三角形，所以其“四心”都在頂角MON的平分線上，即在過O點(diǎn)的同一直線上．

4 關(guān)于原考題(3)“源”的探究

將考題(3)的圖形簡化成等腰梯形，就變成“判斷等腰梯形內(nèi)接菱形”的問題：

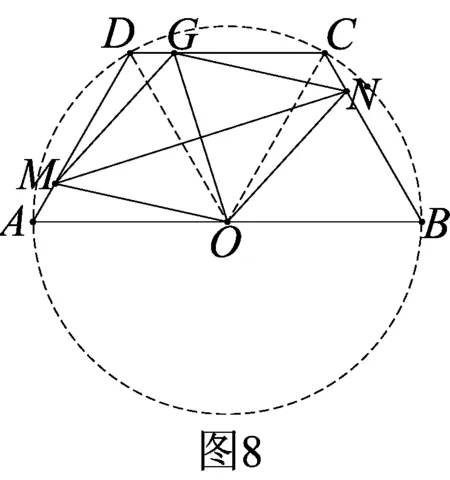
題源探究1如圖8，等腰梯形ABCD的底角∠A=60°，AB為其外接圓的直徑，若AM=CN，O為AB的中點(diǎn)，OG平分∠MON，則四邊形OMGN為菱形．

簡證連接OC、OD．易推△OAM?△OCN,則∠MON=∠AOC=120°，又∠MOG=∠AOD=60°，則∠MOA=∠GOD,于是△MOA?△GOD，故OM=OG，從而△MOG為正三角形，故四邊形OMGN為菱形．

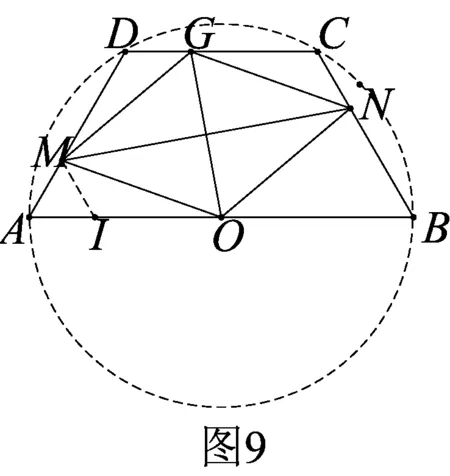
由此可見，上述等腰梯形的內(nèi)接菱形OMGN有無窮多個(gè)，且“AM=CN，O為AB的中點(diǎn)”是它的一個(gè)充分條件．我們自然要問，這個(gè)條件是“四邊形OMGN為菱形”的充要條件嗎？

題源探究2如圖9，等腰梯形ABCD的底角∠A=60°，AB為其外接圓的直徑，若四邊形OMGN為菱形，求證：(1)AM=CN；(2)O為AB的中點(diǎn)．

簡證(1)過點(diǎn)M作BC的平行線，交AB于I點(diǎn)，則MA=MI．又OMGN,OI∥GC，可得△OMI?△GNC，故CN=MI=AM；

(2)假設(shè)O不是AB的中點(diǎn)，取AB的中點(diǎn)O′，由(1)得AM=CN，則四邊形O′MG′N為菱形，故MN有兩條中垂線OG、O′G′，此為矛盾．所以O(shè)為AB的中點(diǎn)．

綜上所述，“AM=CN，O為AB的中點(diǎn)”是“四邊形OMGN為菱形”的充要條件．

至此，我們還會有疑問，在什么樣的等腰梯形中，上述充要條件還成立嗎？

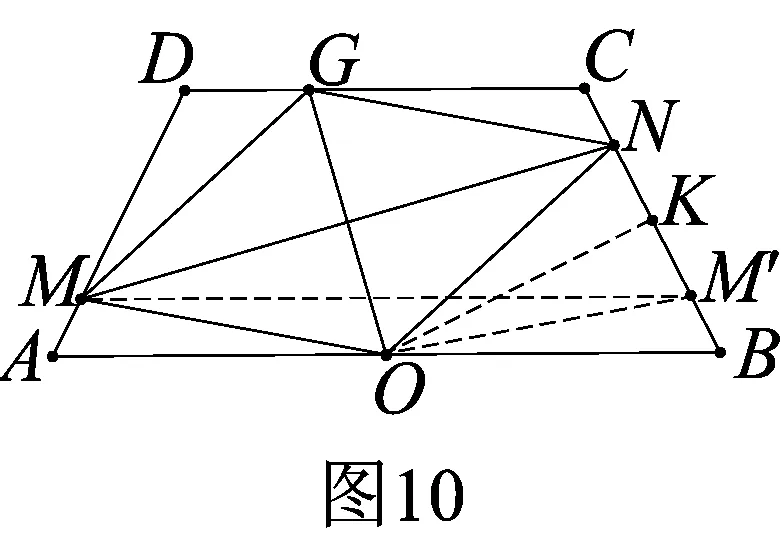
題源探究3如圖10，等腰梯形ABCD中，AM=CN，O為AB的中點(diǎn)，若四邊形OMGN為菱形，探究等腰梯形ABCD應(yīng)滿足什么條件？

解過M作AB的平行線交BC于M′，取BC的中點(diǎn)K，易推BM′=AM=CN,OM′=OA，則KM′=KN,OM′=ON，故OK垂直平分BC，于是OB=OC，即AB為等腰梯形ABCD外接圓的直徑．

于是得到：等腰梯形ABCD中，AB為其外接圓的直徑，OG平分∠MON，則“四邊形OMGN為菱形”的充要條件為“AM=CN，O為AB的中點(diǎn)”.

證明過程與上述探究雷同，這里略去(也可參考后面更一般的情形)．

可見，原中考題(3)是∠A=60°的特殊情形．

但是，我們又有新的疑問，在一般等腰梯形中，“四邊形OMGN為菱形”的充要條件是什么？

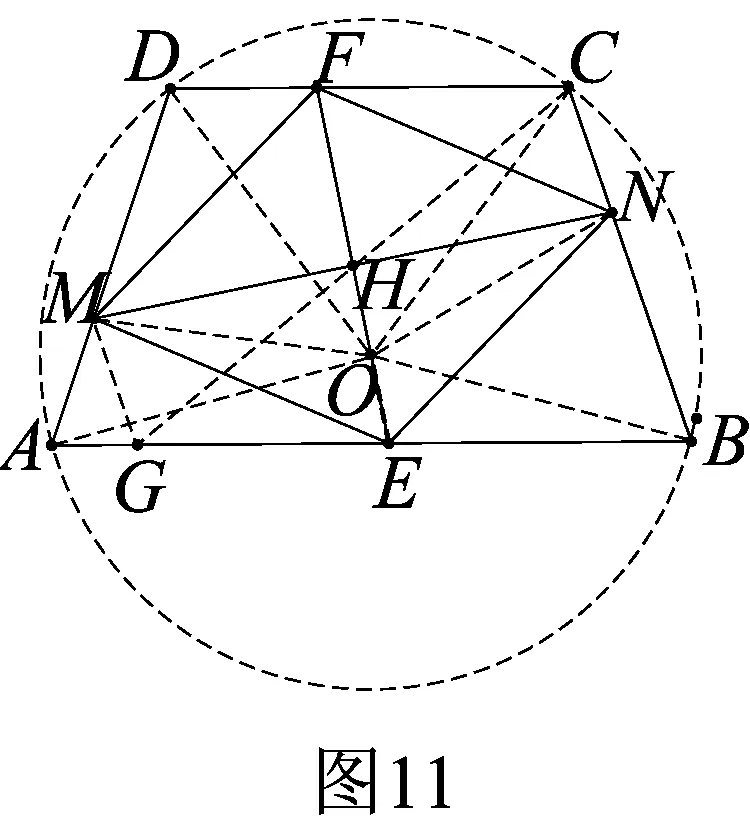
題源探究4如圖11，等腰梯形ABCD中，AM=CN，MN的中垂線與兩底分別相交于E、F，求證：(1)四邊形EMFN為菱形；(2)直線EF過定點(diǎn)(等腰梯形ABCD外接圓的圓心O．)

證明(1)過M作BC的平行線交AB于G，連CG，則MA=MGCN，即平行四邊形CNGM．則CG經(jīng)過MN的中點(diǎn)H，故H為CG的中點(diǎn)，于是H為EF的中點(diǎn)，即MN垂直平分EF,從而四邊形EMFN為菱形；

(2)在圖11中，連OA、OB、OC、OD、OM、ON，因AD=BC,故∠AOD=∠BOC,故∠MAO=∠NOC,易推△MAO?△NOC．

故OM=ON,即點(diǎn)O在MN的中垂線上，即直線EF過定點(diǎn)O．

反過來：如圖11，若等腰梯形ABCD有內(nèi)接菱形EMFN，求證：(1)AM=CN；(2)直線EF過定點(diǎn)(等腰梯形ABCD外接圓的圓心O)．

證明(1)連CH并延長與AB相交于G點(diǎn)，連MG，

因?yàn)镠為MN的中點(diǎn)，所以H為CG的中點(diǎn)，易推MGCN且MG=MA，故AM=CN；

(2)因?yàn)锳M=CN，由前面證明結(jié)論可知，直線EF過定點(diǎn)O．

可見“AM=CN”是“四邊形MFNG為菱形”的充要條件，且內(nèi)接菱形作法是：①在腰AD、BC上分別取M、N，使得AM=CN；②作MN的中垂線．

原中考問題(3)是上述結(jié)論的非常特殊的情形．

4 一般梯形內(nèi)接菱形的充要條件是什么？

同上，我們利用數(shù)學(xué)實(shí)驗(yàn)可以得到下列結(jié)論：

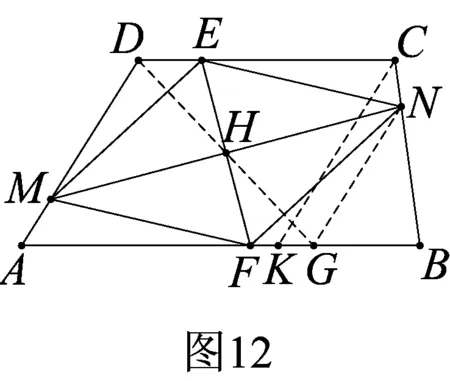
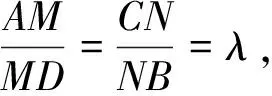
證明過C、N作AD的平行線，分別交AB于K、G,連DG．

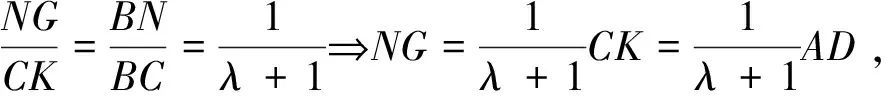
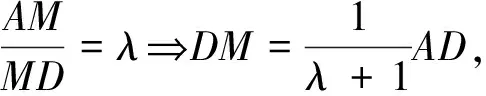
則DMNG，得平行四邊形DMGN，

故DG過MN的中點(diǎn)H，易推H也為EF的中點(diǎn)，即MN是EF的中垂線，

故四邊形MFNE為菱形

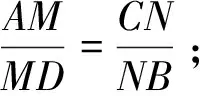
證明延長DH與AB交于G,作CK∥AD交AB于K．

因H為EF的中點(diǎn)，故H為DG的中點(diǎn),又因H為MN的中點(diǎn)，得平行四邊形DMGN.

所以DMNG，故于是可得

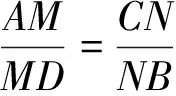
這樣，我們實(shí)驗(yàn)探究得到了原中考問題(3)的最原始的源頭！