基于解釋結構模型的區域衛生信息化影響因素分析

李 彬 王葉婷 向 璨

華中科技大學同濟醫學院醫藥衛生管理學院，武漢，430030

區域衛生信息化是指在一定區域內，應用計算機技術，為醫療衛生服務的提供方、接受方、支付方、管理方以及醫療衛生產品供應商，提供衛生信息的采集、傳輸、存儲、處理、分析、表達，以支持區域衛生管理，為人民群眾提供最佳的醫療衛生服務［1］。隨著區域衛生信息化的發展，這方面的研究逐漸增多，但涉及區域衛生信息化影響因素及相互關系的研究卻寥寥無幾，更沒有通過數理方法去分析因素孰輕孰重。因此，本研究組從系統工程學中選擇解釋結構模型法，整體架構分析影響區域衛生信息化的因素，理清因素間的層次和影響結構，為完善區域衛生信息化現狀提供更加科學而規范的指導。

1 構建區域衛生信息化影響因素的解釋結構模型

解釋結構模型法(Interpretation Structural Model，ISM)是一種系統結構模型化技術，可層次化、條理化和系統化地進行多要素問題的認知和分析，最早由美國Warfield教授于1973年提出。該方法以定性分析為主，能有效明確問題的層次和整體結構，可以把復雜的關系轉化為直觀的結構關系模型。解釋結構模型法主要包括5個步驟:①建立影響要素表;②分析各要素間兩兩關系，建立鄰接矩陣A;③通過矩陣運算，求出可達矩陣M;④通過可達矩陣M進行層次級別劃分;⑤繪制階級有向圖，建立解釋結構模型［2］。

1.1 選取影響區域衛生信息化的要素

在解釋結構模型法之前，首先通過專家咨詢法完成了ISM要素篩選。專家組由教授、副教授、工程師等高級職稱人員12人組成，成員均是衛生信息管理方面的專家，對所要解決的問題有一定的專業基礎和獨到見解。經過專家咨詢后總結歸納出影響區域衛生信息化的17種主要因素，如表1所示。

1.2 設立因素間的邏輯關系，建立鄰接矩陣

影響區域衛生信息化的17個主要因素之間是相互影響和關聯的。設m為影響區域衛生信息化因素的個數，則用m階矩陣表示各要素兩兩關系，即形成鄰接矩陣A［3］，如圖1所示。如果兩要素之間存在直接影響關系，用1表示，否則用0表示。即Si對Sj有直接影響，值為1;Si對 Sj無直接影響，值為0［4］。例如，將要素S1(國家宏觀政策的推動)與S7(標準化體系的實施)進行兩兩比較，S1對S7有直接影響，則在矩陣A中第一行第七列標記值為1，即a17=1;S7對S1無直接影響，則在矩陣A中第七行第一列標記值為0，即a71=0;即表示國家宏觀政策的推動對標準體系的實施有直接影響，反之則無直接影響。

表1 區域衛生信息化的影響因素

1.3 通過矩陣運算，求出可達矩陣M

鄰接矩陣A反映的是各因素之間的直接關系，當然要素之間還存在著間接關系，即用可達矩陣M來表示各因素間存在的直接或間接的影響關系。若存在關系，則用值1表示，即Si對Sj有直接或間接的影響，反之用0表示，即Si對Sj沒有直接的或間接的影響［5］。

根據布爾矩陣運算法則，可以證明:(A+I)2=I+A+A2，其中I為單位矩陣，即對角線元素為1，其他元素為0的矩陣［6］。

如果系統A滿足條件(A+I)K-1≠(A+I)K=(A+I)K+1=M，則M稱為系統A的可達矩陣［7］。

在本研究中，通過4次矩陣運算后發現，(A+I)4=(A+I)3，所以M=(A+I)3為鄰接矩陣A的可達矩陣，如圖2所示。

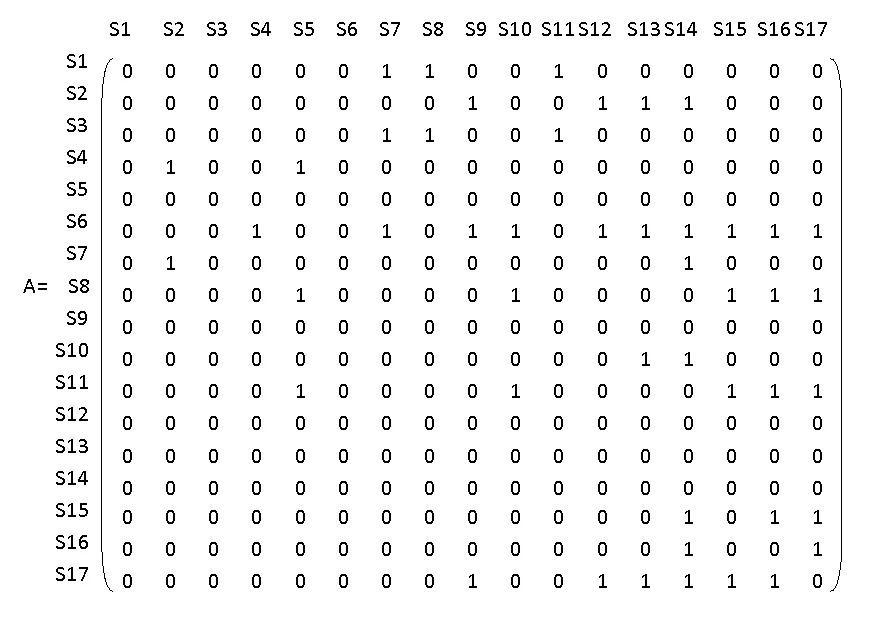
圖1 區域衛生信息化影響因素的鄰接矩陣A

圖2 區域衛生信息化影響因素的可達矩陣M

1.4 通過可達矩陣M，劃分層次等級

根據可達矩陣M可得到可達集合R(Si)、先行集合Q(Si)以及二者交集R(Si)∩Q(Si)。R(Si)是由可達矩陣M中第Si行中所有值為1的列所對應的因素構成的集合，Q(Si)是由可達矩陣M中第Si列中所有值為1的行所對應的因素構成的集合［8］而C(Si)=即為R(Si)和Q(Si)的交集。

第一級的R(Si)、Q(Si)、C(Si)的計算結果如表2所示。若R(Si)=C(Si)，則R(Si)是最高層的因素，根據此法則可確定，表2中 i=5，9，12，13，14 滿足條件，即可刪去可達矩陣中 S5、S9、S12、S13、S14所對應的行和列，則第一級的因素為 S5、S9、S12、S13、S14，抽出后的結果如表3所示。

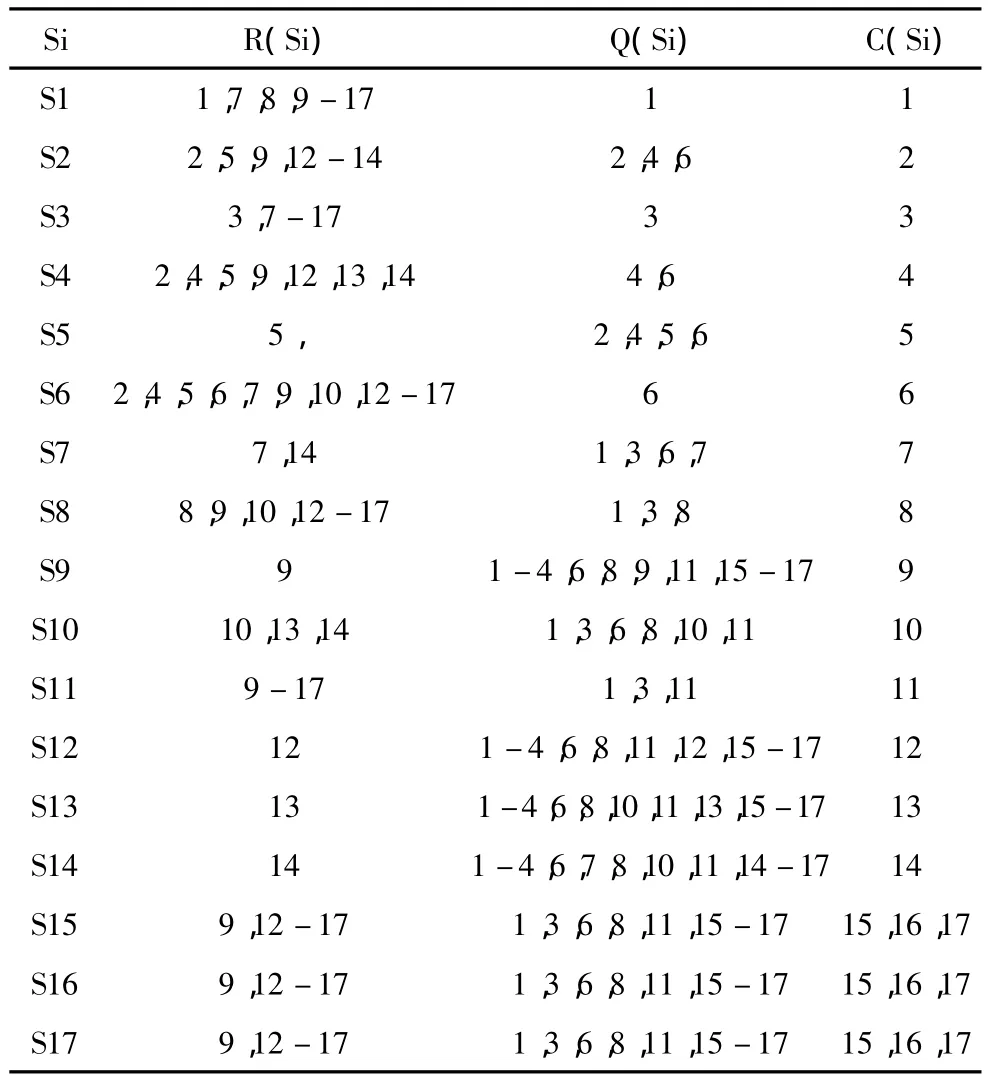
表2 第一級的可達集與前因集

從表3 中可發現 i=2，7，10，15，16，17 滿足條件，即可劃去可達矩陣中 S2、S7、S10、S15、S16、S17所對應的行和列，則第二級元素為S2、S7、S10、S15、S16、S17，抽出后的結果如表4所示。

從表4中可發現i=4，8，11滿足條件，即可劃去矩陣中S4、S8、S11所對應的行和列，從而確定第三級元素為S4、S8、S11，抽出后的結果如表5所示。

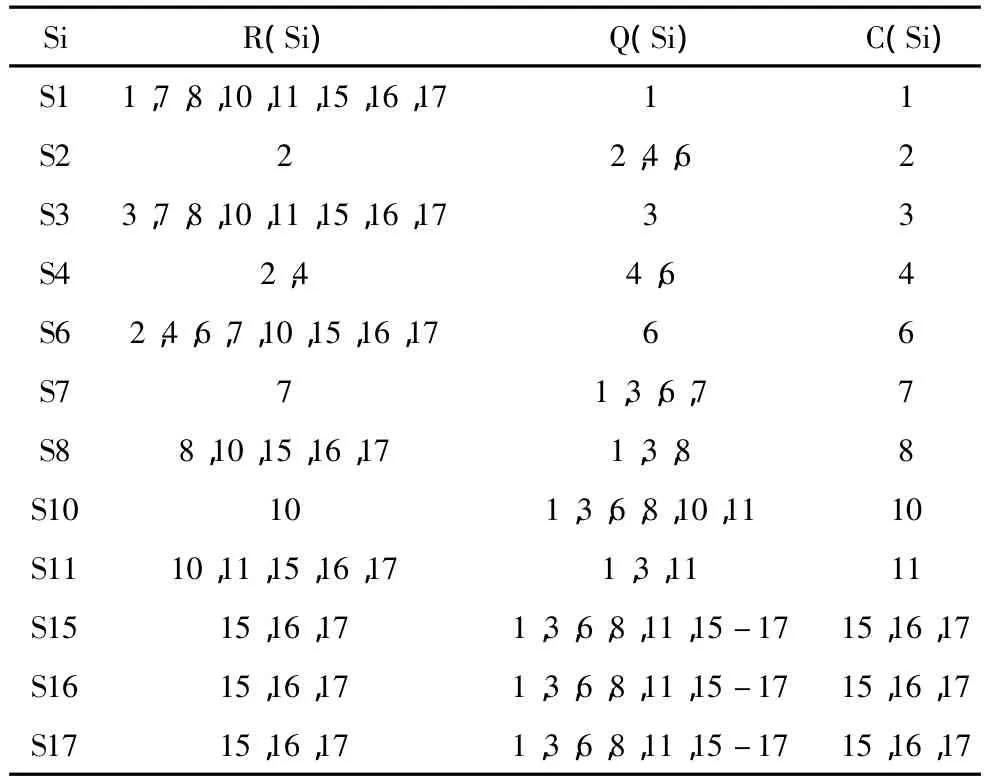
表3 第二級的可達集和前因集

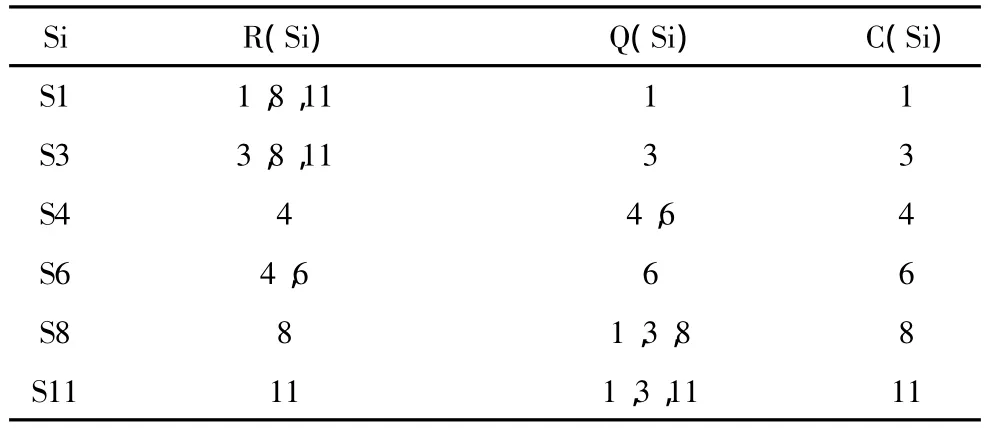
表4 第三級的可達集和前因集

重復同樣的操作，可發現i=1，3，6滿足條件，即最底層因素為S1、S3、S6，如表5所示。

表5 第四級的可達集和前因集

由上述步驟可知，影響區域衛生信息化的17個因素分配在4個級別上，從表2中可以發現S15、S16、S17所對應的行和列的元素完全相同，稱之為強連通塊［9］。

1.5 繪制因素有向圖，建立解釋結構模型

對建立的結構模型進行分析，繪制因素有向圖，如圖3所示，區域衛生信息化影響因素的解釋結構模型具有4層的多級遞階結構，所包含的的影響因素共17項，每一項影響因素通過不同的途徑和方式對區域衛生信息化的成功建設產生影響。

根據解釋結構模型的理論，可將層次遞階結構大致分為3層，即表象層、中間層和根源層。將該理論應用到本模型中，即可得出第一級為表象層，第二、三級為中間層，第四級為根源層［10］。本研究所得的解釋結構模型最底層的影響因素為國家宏觀政策推動、地方政府政策推動、信息技術變革;第三層因素為信息化投資和市場競爭力加強;第二層主要為信息化實施主體內部建設與標準化建設;第一層主要表現為信息化實施主體處理數據與保護數據的能力。

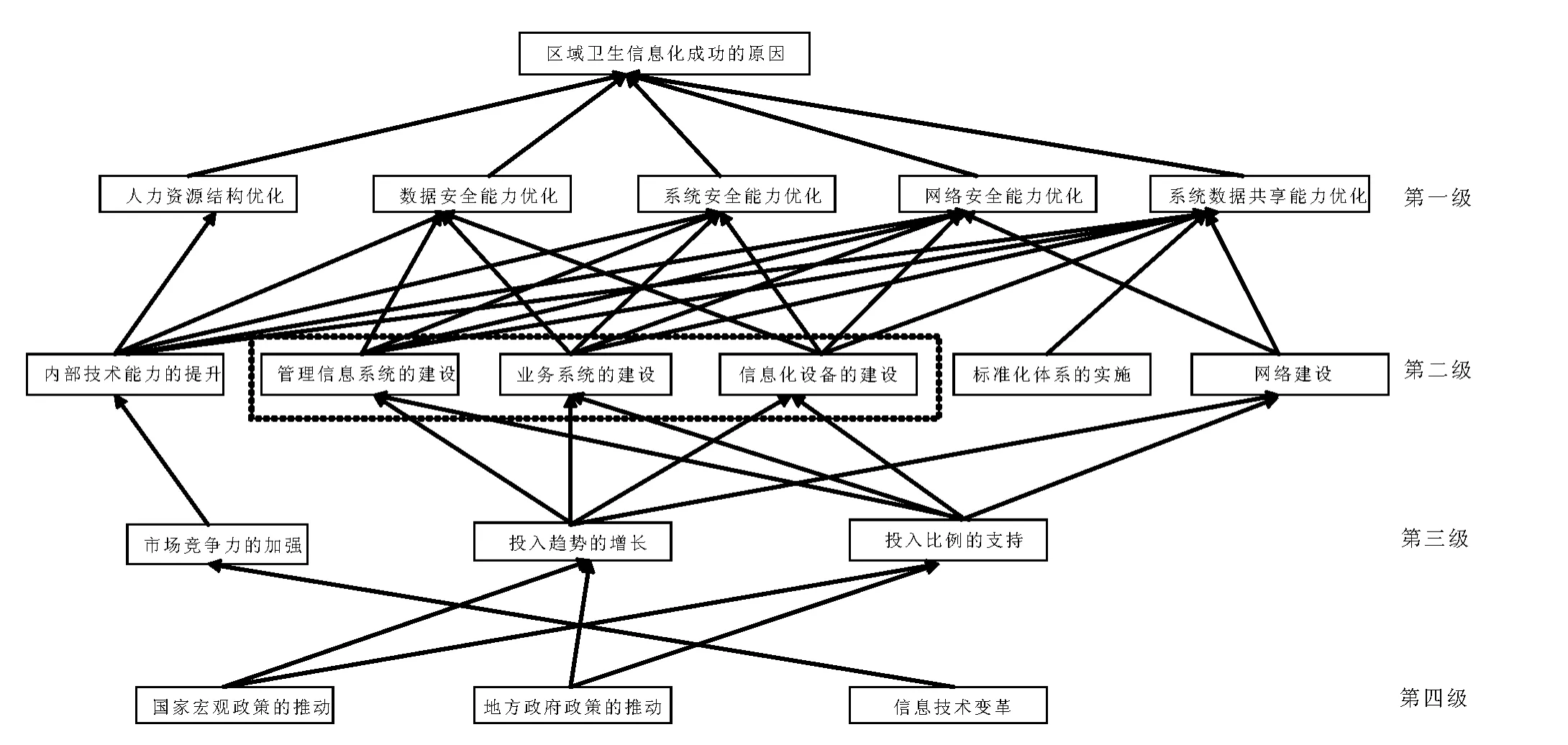
圖3 區域衛生信息化影響因素的解釋結構模型

2 結論

由區域衛生信息化影響因素的解釋結構模型圖可知，17項影響因素呈4級遞進結構，不同層次結構的各項因素相互支撐、相互促進，影響著區域衛生信息化的可持續發展。根源層的3項影響因素，正是引起整個信息化系統的原動力和本質原因，由此說明區域衛生信息化建設的過程中政府的作用是不容小覷的，政府的推動對衛生信息化的跨越式發展發揮著關鍵作用。第三層中的信息化投資是區域衛生信息化建設中的非常重要的環節，它在區域衛生信息化的發展中起著決定性的保障作用。第二層的信息化系統、標準化建設，共同搭建衛生信息化的實務體系。

在區域衛生信息化的建設過程中，要善于從表象因素找到根本因素，只有這樣才能找到改善區域衛生信息化的最著實而有效的方法。我國的區域衛生信息化建設應以宏觀政策為導向，加強頂層設計，自上而下進行規劃建設;而信息技術的變革則是區域衛生信息化成功的最堅實的基礎，只有以先進成熟的信息技術作保障，區域衛生信息化才具有扎實的根基。因此，為促進區域衛生信息化的進一步建設，要抓住這三個最基本的點，根據各地區域衛生信息化不同的基礎，因地制宜地進行引導，以期獲得更好的效果。

［1］王佐卿，王樹山.新醫改模式下區域衛生信息化建設的探討［J］.中國醫院管理，2010，30(11):47-48.

［2］胡振華，蔡新.基于解釋結構模型的高校圖書館館藏紙質資源利用率影響因素分析［J］.圖書情報工作，2010，54(7):46-50.

［3］Jiangyan liu.Analysis of the Factors Influence on Urban E-conomic Development Based on Interpretative Structural Model［J］.Advances in Intelligent and Soft Computing，2011(106):347-351.

［4］Yongxiu He.Risk transmission assessment of electricity price chain in China based on ISM and ECM［J］.Electrical Power and Energy Systems，2013(46):274-282.

［5］Yongsheng Liu.Enterprise Logistics Risk Factors Analysis Based on Interpretative Structural Modeling Method［J］.Advances in Intelligent and Soft Computing，2012(115):617-625.

［6］Jianzhong Xu.On Interpretative Structural Modeling Research of Factors Influencing the Investment Environment in Northeast Old Industrial Base［J］.Management Science and Engineering，2006(6):1151-1154.

［7］Nansheng Pang.The Analysis of the Core Competition of Chinese Construction Enterprise Based on Interpretative Structural Modeling［J］.Knowledge Acquisition and Modeling Workshop，(2008):116-119.

［8］Dingding Xiao.Analysis of Influence Factors of Corporate Technology Innovation Based on Interpretative Structural Model［J］.Industrial Engineering and Engineering Management，2009(9):1943-1947.

［9］Guoqiang Xiong.Interval Number Interpretative Structural Modeling and its Application In Technological Innovation Management［J］.Information Management，Innovation Management and Industrial Engineering，2009(4):156-159.

［10］Hongyan Li.Study on Risk of Enterprise Technology Innovation Based on ISM［J］.Communications in computer and information Science，2011(135):215-220.