還“法則”一個(gè)道理
王淑紅
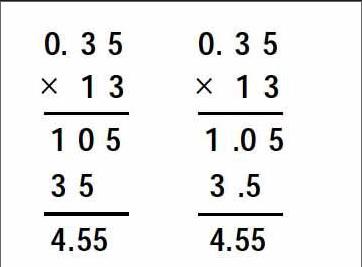
運(yùn)算能力主要是指能夠根據(jù)法則和運(yùn)算律正確地進(jìn)行運(yùn)算的能力。培養(yǎng)運(yùn)算能力有助于學(xué)生理解運(yùn)算的算理,尋求合理簡(jiǎn)潔的運(yùn)算途徑解決問(wèn)題。作為教師,我們更多地應(yīng)關(guān)注學(xué)生思維形成的過(guò)程,使學(xué)生在潛移默化中掌握、理解、應(yīng)用數(shù)學(xué)。
一、在運(yùn)算思維形成過(guò)程中,知其然
布魯納的發(fā)現(xiàn)學(xué)習(xí)論認(rèn)為:“認(rèn)知是一個(gè)過(guò)程,而不是一種產(chǎn)品。”在思維形成過(guò)程中,學(xué)生如果知其然,知其所以然,那么對(duì)知識(shí)的應(yīng)用就得心應(yīng)手了。在“小數(shù)乘整數(shù)”的教學(xué)過(guò)程中,為什么小數(shù)乘法可以用整數(shù)乘法算?這也是筆算時(shí)末尾對(duì)齊的依據(jù)。
1.圖形結(jié)合,更明理
老師用親切的語(yǔ)氣和生動(dòng)的圖片出示義賣活動(dòng)情境,板書小數(shù)乘整數(shù)。學(xué)生把過(guò)程簡(jiǎn)單地寫下來(lái),老師展示其中三種方法:
①小數(shù)的意義:0.2+0.2+0.2+0.2=0.8
②單位換算:整數(shù)乘法0.2元=2角 2×4=8角=0.8元
③
師:怎么想的?(先算2×4然后再加小數(shù)點(diǎn)。)
師:第三種方法也用到了整數(shù)乘法。先算2×4,那道理何在呢?教師出示課件。
師:0.2就是2個(gè)0.1,那4個(gè)0.2呢?就是2個(gè)0.1×4=8個(gè)0.1,用到了整數(shù)乘法2×4。師:那0.25×3呢?
生:25個(gè)0.01×3=75個(gè)0.01用到整數(shù)乘法25×3。
師:那3.5×3呢?
生:想到就是35×3=105個(gè)0.1。
師:3.5怎么變成35?
(教師板書豎式過(guò)程。)積為什么要除以10?
師:好眼熟,積的變化規(guī)律把3.5看成了整數(shù)35。
思考:教師通過(guò)圖形的結(jié)合,結(jié)合小數(shù)意義的教學(xué)為筆算時(shí)末尾對(duì)齊作鋪墊。
2.直擊錯(cuò)誤,免彎路
師:有一個(gè)算式與眾不同。(如左)你有什么想法?
生:我們想整數(shù)乘法35×3就可以了,把3寫到末尾。
師:有沒(méi)有信心挑戰(zhàn)難一點(diǎn)的?0.35×13用豎式算。教師展示(如下)。
師:哪個(gè)更合理?說(shuō)說(shuō)你的想法。(先算整數(shù)乘法35×13,板書35×13豎式過(guò)程,再處理積的結(jié)果。)
師:這個(gè)整數(shù)乘法在小數(shù)乘法豎式中有沒(méi)有應(yīng)用?
學(xué)生完整快速地再寫一次。用自己的方法說(shuō)說(shuō)計(jì)算的方法。
教師板書:小數(shù)乘整數(shù)→整數(shù)乘法。這是轉(zhuǎn)化思想。
思考:教師在巡視過(guò)程中尋找學(xué)生的錯(cuò)誤,但在實(shí)際操作過(guò)程中學(xué)生仍會(huì)出現(xiàn)數(shù)位對(duì)齊、計(jì)算過(guò)程中加小數(shù)點(diǎn)的現(xiàn)象,教師直接出示錯(cuò)誤,在討論中生得出末尾對(duì)齊的方法,這是學(xué)生自我認(rèn)識(shí)改正的過(guò)程,免走了彎路。
二、在運(yùn)算能力訓(xùn)練過(guò)程中,熟其法
1.培養(yǎng)良好習(xí)慣
新課標(biāo)明確指出:數(shù)學(xué)教學(xué)活動(dòng)要注重培養(yǎng)學(xué)生良好的數(shù)學(xué)學(xué)習(xí)習(xí)慣,使學(xué)生掌握恰當(dāng)?shù)臄?shù)學(xué)學(xué)習(xí)方法。在運(yùn)算教學(xué)中培養(yǎng)學(xué)生舉一反三的好習(xí)慣,在利用已有經(jīng)驗(yàn)的基礎(chǔ)上,自主得出運(yùn)算的過(guò)程。當(dāng)然,字跡要清晰,否則會(huì)導(dǎo)致題目抄錯(cuò);計(jì)算細(xì)心,反復(fù)檢查,培養(yǎng)通過(guò)驗(yàn)算檢查正確與否的好習(xí)慣;思路清晰,先算什么,再算什么,進(jìn)位是幾,通過(guò)這些常規(guī)訓(xùn)練來(lái)提高運(yùn)算能力。
2.加強(qiáng)估算意識(shí)
新課標(biāo)要求:在具體的情境中,能進(jìn)行簡(jiǎn)單地估算。加強(qiáng)估算意識(shí),有助于提高計(jì)算的正確率。老師出示錯(cuò)例3.16×15=4.740,學(xué)生先把0去掉,再來(lái)添小數(shù)點(diǎn),在處理積的結(jié)果時(shí),把小數(shù)點(diǎn)點(diǎn)錯(cuò)了,所以,及時(shí)培養(yǎng)學(xué)生的估算意識(shí),對(duì)運(yùn)算結(jié)果快速檢驗(yàn),既方便又省時(shí)。
3.轉(zhuǎn)化形式練習(xí)
熟能生巧,當(dāng)學(xué)生掌握了技能,及時(shí)進(jìn)行鞏固提升,發(fā)散思維。計(jì)算是為實(shí)際生活中解決問(wèn)題服務(wù)的,在具體情境中,教師轉(zhuǎn)化形式提高學(xué)生應(yīng)用能力。如,0.35×13和3.5×13這兩個(gè)計(jì)算方法有什么相同點(diǎn)?都用到了整數(shù)。提問(wèn)學(xué)生哪里看出來(lái)的,還能寫出其他乘法算式嗎?0.035×13,350×13等。通過(guò)找共同點(diǎn),更深刻地發(fā)現(xiàn)整數(shù)乘法中間計(jì)算過(guò)程,也通過(guò)找規(guī)律的形式,提高了學(xué)生對(duì)數(shù)學(xué)學(xué)習(xí)的興趣。
編輯 黃 龍

