破除“相異構想”的羈絆

王曉靜

研究表明，學生在學習之前頭腦里并非一片空白，在日常的觀察和體驗過程中，會形成一些自己的看法，并在無形中養成一定的思維方式。國外研究者將學生在學習之前形成的概念簡稱為“前概念”，而把學生圍繞“前概念”建立起來的一種特有的錯誤思維結構稱為“相異構想”或“不同的概念框架”。“相異構想”對學生的學習有較大的影響，表現在當新知識與學生已有的“相異構想”不同時，可能會被學生排斥、異化，影響其對知識的理解。很多教師在教學時不重視學生“相異構想”的轉變，認為只要把正確的概念傳授給學生，學生的錯誤認識就自然被糾正過來。殊不知，學生先有的“相異構想”是不容易被拋棄的，會頑固地影響其學習行為的理性趨向，如果教師不能幫助學生消除疑惑、解除困擾，將他們從“相異構想”的羈絆中解放出來，學生對知識的正確理解就會受到阻礙，造成“我都講三次了，你還不懂”的現象。因此，教師在教學時應著力改善學生的“相異構想”，有效促進學生的數學理解，以下談談自己在這方面的一些做法：

一、指導實驗操作，讓錯誤變醒悟

教學中，創設適應學生認知需要的操作活動，引導學生開展數學實驗進行探索、驗證，可以讓學生在活動中發現自身的“相異構想”與數學問題之間的矛盾，經歷自我否定的過程，促進數學知識的理解。

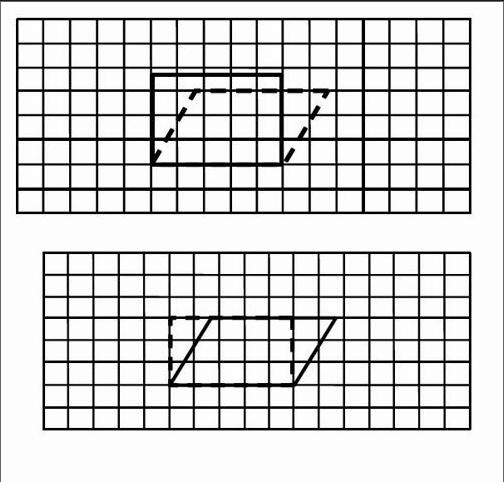
例如，教學“平行四邊形的面積公式”時，受長方形面積計算方法的影響，學生會產生“平行四邊形的面積=底×鄰邊長”的“相異構想”。這時教師可以讓學生操作學具，將一個平行四邊形拉成一個長方形，如圖所示：

學生在操作中會發現平行四邊形拉成長方形后，長方形的長是平行四邊形的一組對邊的長，寬是平行四邊形的另一組對邊的長，用平行四邊形的底×鄰邊的長可以算出長方形的面積。但在拉的過程中面積變大了，原來平行四邊形的面積比拉成的長方形面積小，因此平行四邊形的面積不能用底×鄰邊長來計算。這時，再引導學生在方格紙上畫出與平行四邊形面積相等的長方形。如圖所示：

通過這些實驗，學生會發現與平行四邊形面積相等的長方形面積=平行四邊形的底×高，產生有關平行四邊形面積計算的正確猜想，促進學生對平行四邊形面積公式的理解。

二、運用多種變式，讓局限變全面

有研究者發現，“模擬”在科學概念的發展上扮演著一個極其重要的角色。人們在解決一個不熟悉的問題時，通常會用自己熟悉的類似的事物來詮釋，“相異構想”往往也會在模擬的過程中產生。例如學生在學習2、5的倍數的特征后，以為3的倍數的特征也體現在個位上的數，列舉出了3、6、9、36、93、96……這樣的數。此時，就需要給學生提供一些變式和實例，開拓學生的視野，為學生創設多元化研究的可能，從而擺脫已有經驗的束縛，修正自身的片面認識和錯誤構想。因此在教學時，筆者秘而不宣，讓學生在百數表中圈出3的倍數，學生很快發現百數表里3的倍數個位上分別出現了0-9中的任意一個數。由此，學生很自然地得出判斷3的倍數不能只看個位的結論，去除了只看個位判斷3的倍數的“相異構想”。

在教學《三角形的底和高》時，不少學生認為“底下的邊”才是底，豎直方向的垂線段才是高。為了消除學生的思維定勢，在教學時，筆者用課件將三角形旋轉，讓學生觀察，如圖：

通過觀察，學生發現在旋轉的過程中底和高的位置變了，但位置關系是不變的，因此三角形的底和高不只是水平或豎直的，一個三角形的三條邊都可以看成底并存在相應的高。通過變式，學生很快理解了三角形高的數學本質。

三、利用正向關聯，讓缺陷變建構

奧蘇貝爾認為：“有意義學習過程的實質，就是符號所代表的新知識與學習者認知結構中已有的適當觀念建立非人為的和實質性的聯系。”學生在日常生活和學習中積累起來的經驗是學習新事物的基礎，在正式學習前產生的“相異構想”中也會含有一些可加以利用的因素。此時，應積極在學生已有的經驗與所學知識之間搭建橋梁，以求發揮遷移在學習中的作用，促進學生加速理解和掌握新知。

例如，在教學“倒數”一課時，教師若問學生“什么是倒數”，大多數學生都會猜想“倒數就是倒過來的數”，這是因為根據生理和心理的特點，學生在研究問題時大多著重于外在的因素，所以首先從字面對數的特征進行構想。這樣的構想雖然有一定的缺陷，但也反映了兩個互為倒數關系的分數的外在屬性。教師可以在學生這一猜想的基礎上追問：“0.6與1.6的倒數分別是多少呢？”“6和16的倒數分別是多少呢？”學生可能會想出把這這些數化作分數找出它們的倒數的方法，也可能因這些問題的出現，會讓學生不滿足于僅僅認為倒數就是倒過來的數，產生探求倒數概念本質的欲望，促進其對倒數概念的理解。

四、形成知識結構，讓零散變系統

學生的“相異構想”受制于其生理和心理的特點，會有一些不足，但暗含著學生的諸多探索和思考。如果教師能正確看待學生的一個又一個“相異構想”，尋找構想中的閃光點耐心打磨，這些“相異構想”也會成為一顆顆光彩奪目的珍珠，把它們串聯起來，會幫助學生提升思維品質，促進知識的理解。

例如，在教學“圓錐的認識”時，筆者和學生一起經歷了這樣的學習過程。

師：我們已經認識了圓錐，想一想圓錐的側面展開后是什么圖形？

生1：是三角形！

生2：我同意他的想法，還想補充說明，圓錐的側面展開會是一個等腰三角形。

“噢，”筆者饒有興趣地問，“為什么呢？”

生3迫不及待地要求幫助解釋：“圓錐的頂點到底面圓弧上的點的距離相等，圓錐側面展開后得到一個三角形，它的頂點到底邊上的點的距離也應該是相等的。所以，圓錐的側面展開是一個等腰三角形。”

聽到這樣的解釋，筆者深信學生這一猜想不是僅僅來自于他的直覺，一定經過了比較充分的思考。因為他們已經能夠從曲面中選擇圓錐的母線進行研究，而且發現了母線長度不變的特征。這說明，學生是敢于思考，能夠思考的。

于是筆者問：“等腰三角形的兩條腰相等說明三角形的頂點到底邊兩個端點的距離是相等的，那連接頂點和底邊任意一點的線段長度都相等嗎？”

學生自覺地在等腰三角形中畫出了這樣的線段，很快發現這些線段長度不全部相等。

“怎么辦呢？怎樣的圖形才是圓錐側面展開后的圖形呢？”筆者故作不知。

一段沉默后，生4說：“要找到一種從中心點到周邊任意一點的距離都相等的平面圖形，這樣的圖形才可能是圓錐側面展開的圖形。”

他的回答讓絕大多數學生都點頭稱是，紛紛在紙上比劃，找尋這樣的圖形……經過畫圖實驗，學生最終發現圓錐的側面展開后是扇形。

在這一教學環節中，學生并不缺少發現的眼光，只是沒有能夠抓住平面圖形的特征系統、深刻地思考，離成功發現只有一步之遙。華羅庚先生說過：“學習數學要經過‘由薄到厚和‘由厚到薄的過程。‘由薄到厚是學習、接受的過程，‘由厚到薄是消化、提煉的過程。只有同時經歷這兩個過程，學生才能達到融會貫通、透徹理解，才能抓住統帥全書的基本線索和貫穿全書的精神實質。”因此，在教學中，教師應引導學生將分散、割裂的認識進行整合，形成一個統一的整體，幫助學生構建科學、系統的認知結構，促進學生的構想日趨合理，實現學生對數學知識的自主理解。

德國教育家鮑勒洛夫曾強調：“教育者只能以兒童的先天素質為起點，按其內在法則，幫助兒童成長。”因此，在教學中教師應注意研究學生的“相異構想”，順應學生的學習心理和認知規律，通過智慧地應答、追問、論辯，有效地促進其思維的完善，引導學生科學地理解數學知識，做一個生命的牧者！

責任編輯 林云志