學習《概率初步》注意的問題

陳聚萍

新課程實施以來， 概率內容全面進入中小學課程。從近幾年各地的中考試卷來看， 概率問題已成為中考命題的熱點和亮點，為了更好地掌握這一章知識，在學習過程中應注意下面問題。

一、應弄清概率所研究的范疇

概率是研究隨機事件的數學分析理論，一般地，對于一個隨機事件A，我們把刻畫其發生可能性大小的數值，稱為隨機事件A發生的概率。試驗的特點有兩個：1、出現的結果只有有限個；2、各種結果出現的可能性相等。它的獲取有理論計算和試驗估算兩種。有人會問： “火星上有生命的概率是多少？”這個問題它是一個不知道的現象，它不是隨機現象，所以不是概率研究的范疇。

二、學生對“必然事件”“不可能事件”“隨機事件”概念不清容易混淆

“必然事件”、“不可能事件”屬于確定的事件，“隨機事件”是事先無法確定的事件，在講解這些事件時多舉例，多聯系實際。

例1.成語 “甕中捉鱉”、“拔苗助長”、“守株待兔”、“水中撈月”、“一箭雙雕”是屬于什么事件？此題在學生感到趣味性的同時，加深對概率的認識。

例2.

1、在地球上，太陽每天從東方升起。（必然事件）

2、一元二次方程x2+2x+3=0沒有實數解。（必然事件）

3、用長為5㎝、5㎝、11㎝的三條線段能圍成一個三角形。（不可能事件）

4、有一匹馬奔跑的速度是70㎞/s。（不可能事件）

5、2015年1月1日我市會下雨。（隨機事件）

6、射擊運動員射擊一次，命中十環。（隨機事件）

三、把概率和頻率混為一談

頻率是指每個對象出現的次數與總次數的比值；而概率是指大量重復試驗中，利用頻率m/n的穩定值估計概率，不能說頻率等于概率。概率是伴隨隨機事件客觀存在的，只要有一個隨機事件存在，那么這個隨機事件的概率就一定存在；而頻率則依賴于具體的試驗，它隨著試驗次數的變化而變化，雖多次試驗頻率能穩定其理論概率，但它是一個近似值，接近而不相等，兩者之間總有一定的偏差，且它們是兩個不同的概念。

四、概率的求解容易出錯，不會選擇適當的方法

1、對于一些問題，需把所有的情況一一列舉出來。

例.擲兩枚均勻的硬幣，一枚硬幣正面朝上，一枚硬幣反面朝上的概率是多少？

學生立即回答：“1/3。”學生腦海里想到“正正”、“正反”、“反反”三種情況。實際上，本題目應耐心地列出“正正”、“正反”、“反正”、“反反”四種情況，那么一枚硬幣正面朝上，一枚硬幣反面朝上的概率是“1/2”。

2、學會使用列表法和樹形圖法。

（1）當試驗包含兩步時，列表法比較方便，當然此時也可用樹形圖法。

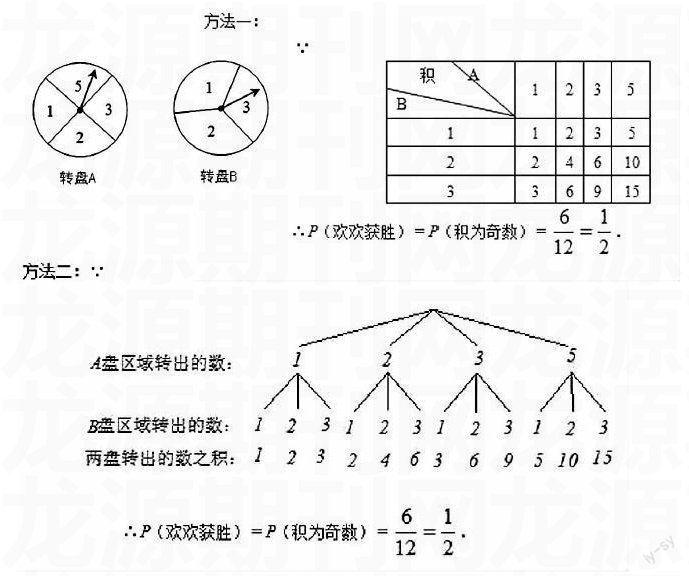
例：轉盤游戲：分別把帶有指針的圓形轉盤A、B分成4等份、3等份的扇形區域，并在每一小區域內標上數字（如圖所示）.歡歡、樂樂兩人玩轉盤游戲，游戲規則是：同時轉動兩個轉盤，當轉盤停止時，若指針所指兩區域的數字之積為奇數，則歡歡勝；若指針所指兩區域的數字之積為偶數，則樂樂勝；若有指針落在分割線上，則無效，需重新轉動轉盤。

a：試用列表或畫樹狀圖的方法，求歡歡獲勝的概率； b：請問這個游戲規則對歡歡、樂樂雙方公平嗎？試說明理由。

（2）當試驗在三步或三步以上時，用樹形圖方便，此時，不宜列表。

例：經過某十字路口的汽車，它可能繼續直行，也可能向左轉或右轉。如果三種可能性大小相同，三輛汽車經過這個十字路口，求下列事件的概率：

a：三輛車全部繼續直行；

b： 兩輛車向右轉，一輛車向左轉；

c： 至少有兩輛車向左轉。

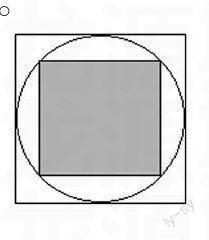
3、利用所占面積的百分比求相應事件的概率。

例：如圖，小凱隨意向水平放置的大正方形內部區域拋一個小球，則小球停在小正方形內部（陰影）區域的概率為： 0.5

4、用頻率估計概率。

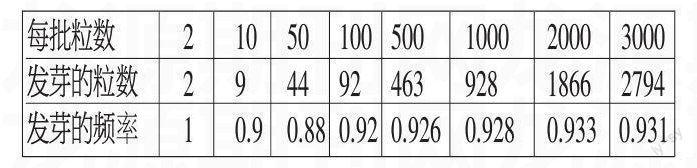
例：某種綠豆在相同條件下發芽的實驗結果如下表，根據表中數據估計這種綠豆發芽的概率約是（保留三位小數）。

解析：隨著試驗次數的增加，頻率呈現出一定的穩定性。所以，這種綠豆發芽的概率約是0.931。

總之，在《概率初步》這一章學習中，多設置與現實生活緊密聯系的問題， 讓學生在解決實際問題的過程中感受到概率知識與實際生活的緊密聯系， 初步感受概率的思想， 進而體驗概率在進行解決實際問題的作用。掌握以上內容，對概率題目就能迎刃而解。