有效復習再提升 轉變觀念促發展

賀娟

在實際教學中，復習課演變成了滿堂練、滿堂講、滿堂考的無效訓練場。如何改進復習課教學，提高課堂效率呢？

一、轉變復習觀念，突出主體地位

復習的過程是學生對已學知識進一步梳理、補充、內化、再生成的過程。在學習過程中，新知識已經不同程度地在學生腦海建構，學生掌握知識的情況已經形成差異性。此時，如果只是簡單梳理、強化，或者不分主次“眉毛胡子一把抓”，顯然不符合認知規律。

教師要準確把握復習課的任務，認真領悟復習課的功能，充分呈現復習課的特點，立足學生基礎，加強復習課研討，努力打造有效、平實、厚重的數學課堂。學生在復習時對知識掌握情況的差異性，決定了復習的過程也有差異性，這需要教師放手讓學生自己獨立或通過小組合作去完成，明確復習目標，把復習的主動權還給學生，讓學生主動參與。復習，是一項再認識的過程，這需要有對知識體系全面把握的能力，及對學習的鉆研精神，教師要引導學生自主整理，構建知識網絡，促進知識系統化，使學生對以前所學的知識有新的認識。復習，還能培養學生自覺性。主動求知才能得到提高，故復習能發展學生自主學習的能力，培養其概括能力，更培養他們自主學習的良好習慣。

二、立足學生基礎，整合教學資源

建構主義理論告訴我們，對知識的理解是建立在學生原有知識基礎之上的。在對已學內容進行復習時，教材作為教學的重要資源，如何使學生在熟悉的同時產生新鮮感，對學習材料重新產生興趣，就需要作為主導者和服務者的教師，根據學生實際情況，對教材進行恰當的整合，以生成新的教學資源。

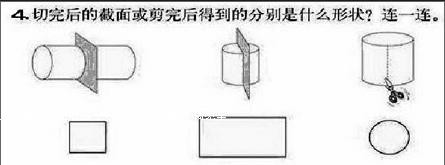
例如，小學數學六年級下冊20頁第4題，將立體圖形切開后的截面或剪開后得到的側面與平面圖形連線。（如下圖）

在新授時練習的目的是發展學生的空間想象能力，在復習階段可以進一步利用和開發這一教材資源，進行圓柱表面積和體積的綜合運用，創造這樣的問題情景：第一個長20厘米的圓柱，經過切割后表面積增加18平方厘米，原來圓柱的體積是多少？第二個底面直徑8厘米的圓柱沿直徑作垂直于底面的切割后，表面積增加了32平方厘米，原來圓柱的體積是多少？

像這樣“舊瓶裝新酒”，學生對經歷過的情境首先產生心理相融，但進一步分析后發現，出現了新的探究問題，學生在“還有這樣的變化”的疑問中，激發了新的探究興趣，思維達到一個新的高度。

三、重組知識結構，構建知識體系

我們說復習課要解決的是知識點的點、線、面三者結合的問題，承載著溝通與生長的獨特功能，它不是對舊知的簡單重復再現，而是要使學生在原有知識基礎上產生新的、系統化的理解與認識，在“溫故”的過程中，達到“知新”的高度。這里的“新”，并非新的知識點，而是結構、系統之“新”，是理解、運用之“新”。

例如，數的整除的有關知識：因數與倍數、質數與合數、公因數與最大公因數、公倍數與最小公倍數、互質數等概念教學，是分散在五年級下冊《分數的意義與性質》單元中完成的，與約分、通分相關聯。六年級下冊的《整理與復習》單元，則將這些知識點系統歸類于“數與代數”的體系中進行整理。與原來所學相比，知識的生長點和結構都發生了很大的變化，在復習課時怎樣幫助學生重新理解這些概念之間的聯系，建立知識體系，就要求教師對知識進行重組，幫助學生形成新的知識結構，建構新的知識體系，使學生更深刻地理解知識，更好地運用知識，達到新的學習高度。從方法基礎到數論體系，將知識進行重組，打造厚重的數學課堂。

（作者單位：武漢市蔡甸區奓山中心小學）