初中數學課堂有效提問的探索與思考

熊方亮

摘要：問題是開啟學生思維，促進學習有效學習的重要手段。綜觀當前課堂教學現狀，課堂提問華而不實，流于形式，效果不佳，難以充分調動學生，促進學生綜合發展。因此，在初中數學課堂教學中，教師要不斷思考與探索，優選有效方法，做到有效提問，從而構建高效靈動課堂。對此，筆者結合自身教學實踐，對初中數學課堂有效提問提出了自己的幾點建議，以作拋磚引玉。

關鍵詞：初中數學；課堂提問；有效性

中圖分類號：G633.6文獻標識碼：A 文章編號：1992-7711（2015）15-060-2

一、關注實際，有效提問

課堂提問是服務于教學內容與教學目標的，在進行問題設計時，教師要關注實際，靈活有效提問，以明確學習目標，啟迪學生積極思維，培養學生問題意識。

首先，要注意問題的指向性，明確提問目標。教師要充分關注學生實際情況，從學生已有知識經驗出發，圍繞教學目標，緊扣教學內容，靈活提問。

比如，學習蘇科版七年級上《合并同類項》后，在進行課后小結時，教師不應按照常規提問：“同學們，我們今天探討了什么內容？你學到了什么？”這樣的問題范圍太廣，目標性過大，有的學生思維如脫韁野馬，一放不可收拾，有的學生卻無從回答。倘若教師規定或限定范圍，將問題空間與目標合理縮小，更有助于啟迪孩子思維，喚醒學生知識與經驗。

如判斷下列各組中的兩項是不是同類項？為什么？①02x2y與2x2y；②4abc與4ac；③2m2n與2mn2；④-125與12；然后提問：同類項的分類需要注意什么事項？這樣，問題更有指向性，更能誘導學生快速思考。學生口答后總結三條注意事項：①兩個相同：字母相同，相同字母的指數相等；②兩個無關：與系數無關，與字母順序無關；③所有的常數項都是同類項。

其次，要注意提問的思維性，激活學生思維潛能。在課堂教學中，有些教師單純為活躍氣氛，或看低學生能力，而提出大量欠缺思維性的問題，學生看似配合答問，但沒有得到思維發展。

因此，在初中數學教學中，課堂提問要有思維深度，緊扣知識重難點或疑點，并考慮學生實際與現實生活，巧設開放性、適宜的、新穎的、有坡度的問題與情境，驅動學生思考，使其以原有知識與經驗為基礎進行主動建構，提高教學有效性。

二、尊重差異，分層提問

學生個體之間存在一定的差異，因此，教師在進行提問的過程中，要充分考慮學生的個性差異，尊重學生個體差異，結合學生學習基礎、學習能力以及思維水平的不同，巧設層次性的問題，做到因材施教，分層提問，盡可能讓每位學生都有所收獲、有所提高、有所發展，從而增強學生學習信心。需注意的是，教師在設計分層問題時，要把握好問題的難度和梯度，問題難度既不可太大，否則部分學生無從入手，惘然無所得，也不可太淺顯，否則難以啟發學生思維，而應有針對性的、有層次性的提問，由淺入深，由易至難，循序漸進，層層遞進，以促使學生主動參與答問，積極思索起來，促進學生的共同發展。

譬如，學習蘇科版七年級下《因式分解》后，筆者結合學生實際水平和認知規律，設計了以下分層問題：

A組：把下列各式因式分解：（1）3ax2-3ay4（2）-2xy-x2-y2（3）3ax2+6axy+3ay2

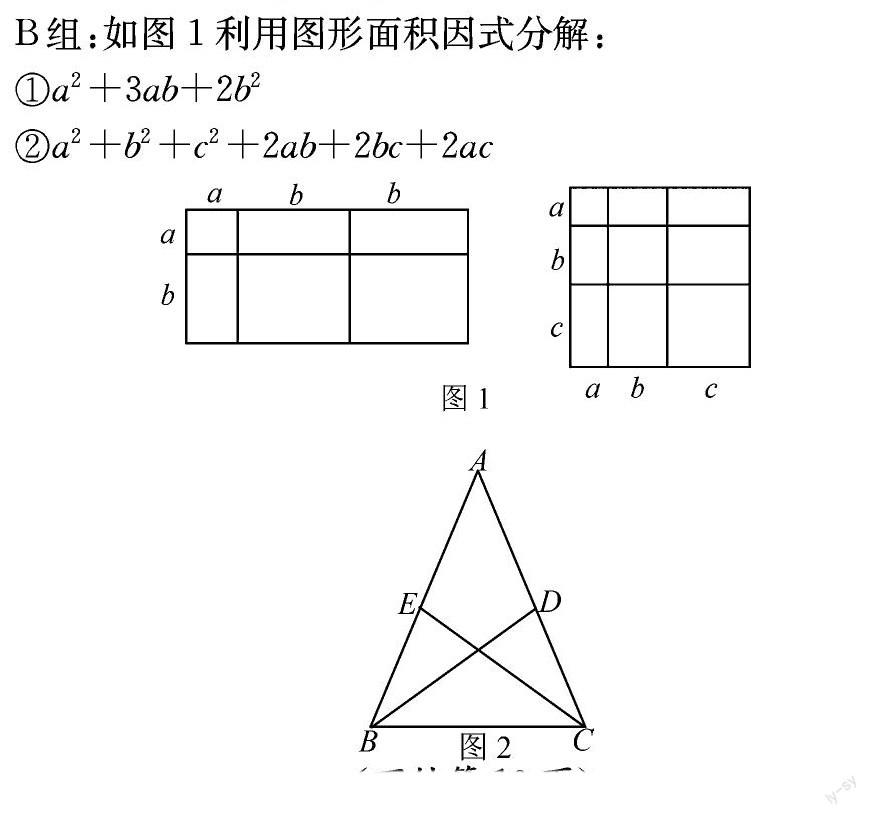
B組：如圖1利用圖形面積因式分解：

①a2+3ab+2b2

②a2+b2+c2+2ab+2bc+2ac

C組：①請你從下列各式中，任意選擇兩式作差，

并將得到的結果因式分解：9a2，（x+y）2，1，4b2；

②請寫出一個三項式，使它能先提公因式，再運用公式法來因式分解，你編的三項式是，分解因式的結果是。

其中A組為基礎性問題，B組為提升性問題，C組為拓展性問題，然后要求學生根據自身學習情況自主選擇問題，進行參與作答，以滿足不同層次學生的學習需求，讓學生體驗成功的喜悅，增強學生學習自信心。

三、變換角度，發散提問

發散性思維是學生要具備的思維品質之一，是培養學生創新能力的重要途徑。教學實踐表明，學生數學思維能力靈活與否與學生的發散性思維有著緊密聯系。學生在解決問題的過程中，往往容易受思維定勢的影響，拘泥于既定方法與模式，因而無法使問題得到高效解決。因此，在初中數學課堂提問中，教師要注意打破定勢思維，變換問題角度，發散提問，從而促使學生多角度、多方位探索問題、分析問題、解決問題，培養學生思維的發散性、靈活性以及敏捷性，增強學生多向思維能力。如，教師在進行概念、法則、定義、公式、定理教學時，可以從不同的角度提出問題，引導學生多層次、多方位的去理解和運用；在進行習題教學時，可以通過一題多解，一題多變，一題多問等方式，訓練學生多向思維能力，提高學生解題能力。

例如，蘇教版八年級上P29例2經濟習題中，筆者通過設置發散性問題，通過一題多問，培養學生思維發散性和靈活性，提高學生多角度、多方面思考、分析、解決問題能力。

例1：如圖2所示，在△ABC中，已知AB=AC，兩條角平分線BD、CE交于點O，請問：OB與OC是否相等？請說明理由。

變式1：若此題條件保持不變，請問OD與OE是否相等？BD與CE是否相等？為什么？

變式2：若此題中條件AB=AC保持不變，BD、CE分別為AC、AB上的中線，則OB與OC是否相等？OD與OE是否相等？BD與CE是否相等？請說明理由。

變式3：若此題中AB=AC這一條件仍保持不變，BD、CE分別為AC、AB上的高，則是否存在以下關系：OB=OC，OD=OE，BD=CE？請說明理由。

四、適時等待，深度回答

在課堂教學中，有些教師太過關注教學進度，急于得到正確答案或結論，因而學生答問時教師等候時間較少。如提問后，往往是“一問即答”，當某位同學答題受阻或回答沒有接近預期答案時，便急著轉問他人，轉問無果時，老師干脆自圓其說、自問自答。在如此情況下，課堂提問又如何能發揮真正教育意義與作用，怎會促進學生思維發展，培養學生科學素質，甚至還會影響學生學習積極性。

事實上，在教學過程中，等待也是一種藝術，合理而恰當的等待，給學生充足思考時間，促使學生深入思考、主動探尋，形成意想不到的、令人驚嘆的精彩回答，獲得自豪感，提高學生學習興趣。反之，學生基礎再好，若欠缺思考時間，也難以快速形成有深度的回答。因此，在初中數學課堂提問中，教師要注意等待藝術，留出充足的等待時間，讓課堂綻放出燦爛的智慧火花，促進有效提問。

如：教學蘇科版七年級下《探索平行線的性質》時，筆者創設情境，提問引思：

如圖3，工人在修一條高速公路時在前方遇到一座高山，為了降低施工難度，工程師決定繞過這座山，如果第一個彎是左拐30°，那么第二個彎應朝什么方向，才能不改變原來的方向。

問題一出，教師并沒有急著讓學生回答，而是在等待，讓學生認真觀察、自主探究、小組合作、交流討論，主動獲取新知。另外，在學生答問時，教師也要給其留出一定組織語言與調整答案的時間，并耐心聆聽，靈活啟發。

總之，課堂提問是一門藝術，也是一種智慧，它對于調動學生探究動機，激活學生思維，提高學生學習能力有著積極的作用。在平時教學過程中，教師要充分結合課程特點、學生心理特征以及認知規律，圍繞教學目標，優化問題設計，從而啟迪學生智慧，碰撞學生思維，讓學生愛學、樂學，使課堂走向有效、高效。

（本文為江蘇省“十一五”規劃課題：農村初中數學課堂中主體參與探究的實踐研究（編號：D/2013/02/625）階段成果。）