小學數學教材要厘清邏輯順序

張奠宙

平行和平移，都是小學數學中的幾何學名詞。二者之間存在著內在的邏輯順序，即先有平行，才有平移。小學數學盡管需要深入淺出，卻不宜違背這一邏輯順序。

讓我們看某現行教材中關于平行直線的定義。

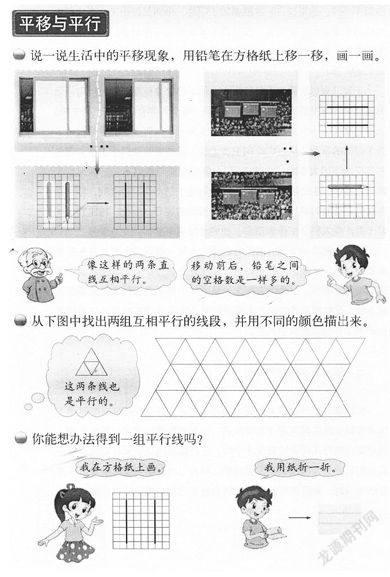
這一段教材，通過移動的門窗、上升的國旗，以及鉛筆的水平移動的觀察，就說“像這樣的兩條直線互相平行”。顯然，這是從物體的平移，給直線的平行作定義式的陳述。這樣處理，會出現不少問題。

首先，門窗、國旗都是立體或平面的實體，抽象之后，乃是二維的平面，怎樣和一維的“直線”聯系起來呢？像國旗升起的畫面中，平行線在哪里？不加以明確指出，讓學生如何理解編寫意圖？

其次，若從兩支鉛筆抽象為幾何圖形，不過是一條線段，怎能說是直線呢？線段和其所在的直線，需要有所區分。這里的斷語，應該是“像這樣的兩條線段互相平行”。至于說這也是它們所在的兩條直線互相平行，那是另一種約定，在界定一個對象時要分清楚，不能混同起來。

第三，最為嚴重的混淆是用平移來界定平行，把二者的邏輯順序弄顛倒了。說到底，究竟是先有“平行”，還是先有“平移”呢？

先來看什么是平移。百度詞典這樣定義：

“在平面內，將一個圖形上的所有點都按照某個方向作相同距離的移動，這樣的圖形運動叫作圖形的平移運動，簡稱平移。”

這里的一個關鍵詞是“所有點按同一個方向”，它的意義就是每組對應點連成的直線都彼此平行。這就是說，教材圖上那支平移的鉛筆，其上的每個點都要沿“水平方向”移動一個固定的距離。如果將鉛筆頭移動前后兩點的連線線段（記為ab），鉛筆底部點前后形成的兩點連線（記為cd）那么因為是同一方向，所以必須有ab∥cd。這時，abcd四點構成一個矩形。進一步，那支鉛筆也可以沿45度角向“東北”方向平移，鉛筆各點掃過的圖像就是一個平行四邊形。

這就是說，作平移運動時，圖形中無限多的點都要保持“同一方向”，也就是要形成無限多條的平行線。因此，先有平行概念和平行判斷準則，才能作平移運動。用平移定義平行，在邏輯上有誤，混而有錯。

在這頁教材上，還可能會產生另外一些誤解。

1.以為可以用兩條線段彼此間是否為平移來判斷是否平行。但這是做不到的。事實上，判斷兩線段是不是平移，必須把平移的那個“統一方向”找出來。為了找這個方向，最后不得不依賴同位角相等的那些平行線判定法則。因此，想用平移概念，繞開平行線的嚴格定義和判別準則是做不到的。

2.教材的那兩支鉛筆，是向水平方向和垂直方向平移。容易產生的錯覺是，平移就是水平方向的移動，或者是垂直方向的移動。這就會造成平行線都是水平的或垂直的錯誤印象。

3.教材呈現的平移操作，只能在方格紙上向水平或垂直兩個方向移動。 那么，要在方格紙上作45度、60度方向的移動怎么辦？教材沒有交代，也無法說清楚。

綜上所述，用線段平移來界定線段平行， 在邏輯上有誤，既不能實際操作，又會帶來一些誤解，應予修正改進。

筆者認為，平行線教學要和“方向”概念聯系起來，用直線的方向相同來定義直線的平行，即用直觀的、相當于同位角判定準則的情境來進行處理，那要另文探討了。

（華東師范大學數學系 ? 200241）