例談小學數學教學中數形結合思想的滲透

易玲

在小學數學教學中，數與形是兩條貫穿始終的主線。數形結合既是重要的數學思想，又是解決數學問題的重要方法。在教學中有意識地向學生滲透數形結合的思想對數學學科的后續學習，乃至學生的終身發展都具有十分重要的意義。本文筆者結合教學實踐，談談自己的想法。

一、在數的概念教學中滲透數形結合思想

數的概念教學是小學數學教學中的重要內容，是形成數學知識體系的基礎。然而對于小學生來說，數學概念是抽象的，因此，教師應充分利用圖形，將圖形的形象與概念的抽象建立聯系，用恰當的圖形演示數學概念中最本質的屬性，豐富學生的感性材料，從而為學生建構數學概念奠定基礎。在課堂教學中，通過數與形的不斷轉化，引領學生經歷概念的形成、概念的理解及概念的應用三個階段，使得學生對于概念由感性的表象發展到理性的概括理解。

如在“分數的初步認識”一課的教學中，可借用多種圖形材料去幫助學生認識分數，初步感悟分數的含義。首先教師在創設情境中讓學生創設符號來表示“一半”，有圖形語言，有文字語言，有符號語言，如、、等，在對比與交流中不僅要讓學生體會符號語言表示的優越性，同時也要能借助圖形語言去引導學生初步認識分數。

其次，在揭示分數概念之后，引用歷史材料等圖形史實，展示各個不同年代分數的表示方法，讓學生感受分數的產生、發展過程，更重要的依然是用充分的“形”去理解分數的含義。

比如分數，古代的中國人、埃及人以及阿拉伯人表示的方式都各有不同。

古代中國人算籌表示法 ? ?古代埃及人表示法 ? ? 阿拉伯人表示法

直到印度人發明了“—”，就成為了我們現在所通用的表現形式了。

最后采用線型模型豐富學生的認識表象，設計在數軸中尋找分數位置的聯系。除了用以鞏固學生對分數含義的理解外，還為學生全面理解分數的含義提供多種直觀支持，將分數與整數的關系建立起整體表象，幫助學生建構與完善知識體系。

在小學階段的數學學習中，有諸多關于數的概念的內容，如小數、百分數等，教師要充分挖掘、利用圖形的特質，讓“形”成為教師教學的得力助手，用“形”去闡述“數”的知識本質，溝通數學知識之間的內在聯系;也讓“形”成為學生思維發展的“腳手架”，促進學生對概念的認知從具體形象的層面向理性感知的層面過渡。

二、在數的運算教學中融合數形結合思想

在計算教學中，引導學生關注算法背后的算理，實現算理與算法的交融是教師教學的重要關注點。教師要有意識地在數的運算教學中融合數形結合思想，用看得見、摸得著的實物，直觀形象地演示算理，幫助學生以形促思，以形助數，從而實現由算理到算法的過渡。

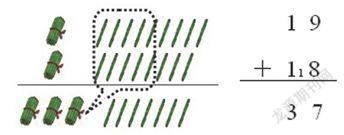
如在“兩位數加兩位數進位加法”一課的教學中，教師引導學生先用小棒擺一擺、算一算19+18，再結合小棒圖，引導學生一步步說出豎式計算的過程，用擺小棒與列豎式并行的方式去演繹“滿十進一”的算理。

在這里，直觀操作是為了解決學生計算中遇到的障礙，體現了以“形”助“數”的必要。在直觀操作的基礎上讓學生抽象出豎式計算的過程。而在之后的教學中，教師沒有把直觀圖丟到一邊，而是引導學生反思整個過程，尋找豎式計算的每一步與直觀圖中的哪一部分有聯系，了解直觀圖與豎式計算的內在關系。因為豎式計算的每一步都有直觀圖的支撐，所以學生能形象地理解“滿十進一”的算理，實現算理與算法的交融。

又如在分數乘、除法的一系列教學中，教師始終可以用長方形紙片作為素材，讓學生通過“分一分、涂一涂”的操作，將“數”的問題轉化為對“形”的分析，從而借助圖形語言理解分數乘、除法的算理。因此，將數形結合的思想融合到運算教學中，能有效尋找數與形的聯系，充分揭示計算方法的本質，為溝通算理和算法服務。

三、在解決問題教學中運用數形結合思想

（一）用“數形結合”化復雜為簡單，理清數量關系

數量關系是數學所特有的研究對象，《義務教育數學課程標準（2011年版）》明確提出要“從現實生活或具體情境中抽象出數量關系”。在一些解決問題教學中，數量關系是教學的重點、難點，因其數量關系多且繁，學生掌握起來十分困難。如果充分運用數形結合思想，巧妙運用線段圖等恰當的圖形直觀地表示其數量關系，常能產生意想不到的效果。

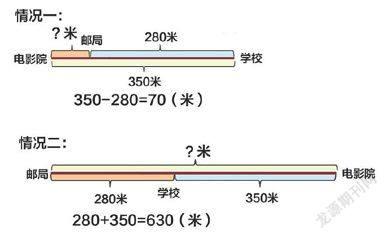
如解決“郵局、電影院和學校在創業大道的同一邊。郵局距學校280米，電影院距學校350米。郵局距電影院多少米？”這一問題時，大部分學生只有一種答案，280+350=630（米）。教師如果能引導學生用畫線段圖的方式表達題意，學生就會有疑惑：郵局、電影院和學校應該在什么位置呢？用線段圖就能清楚、直觀地表示出兩種不同的情況（如下圖）。

直觀的線段圖不僅可以吸引學生的興趣，更重要的是可以幫助他們在適當的圖形中讓復雜問題簡單化，抽象問題形象化，利于學生抽象出數量關系，建構基本的數學模型，有效提高解決問題的效率。

（二）用“數形結合”化抽象為直觀，巧妙解決問題

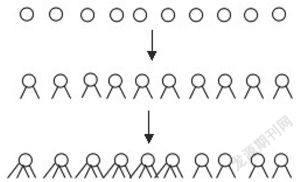
如雞兔同籠問題——已知雞和兔一共有10只，一共有32條腿，求雞兔各有幾只？這類題目的解決方法很多：（1）列方程解答，（2）枚舉法，（3）假設法。但是，對于小學生而言很多方法受到了限制，比如中低年級學生不會用方程，無序的枚舉容易導致枚舉不全面，假設法的數量關系很抽象，學生難以理解。用什么樣的方法讓低年級的學生也可以解決這個古老的難題呢？其實充分運用“數形結合”就能巧妙地解決這個問題。用圓表示10只動物。假設全是雞，則每只雞有兩條腿，把腿畫出來，只有20條腿，但還有32-20=12條腿沒畫。如果每只再添2條腿，這樣還得添12÷2=6只，得出兔子有6只，雞有4只。

在類似的教學中，都可以讓學生畫直觀圖的形式，通過借助直觀圖這種“數形結合”的方式來使得看似抽象的問題直觀化，這顯然更符合小學生以具體思維為主，并逐步向抽象思維過渡的思維特點，從而讓解決問題變得輕松自如，且保護了學生的學習信心，激發學習興趣。

總之，在小學數學教學中，教師應有意識地強調和滲透數形結合的思想和策略，以“形”的直觀表達“數”，以“數”的精確研究“形”，將抽象變具體，把無形變有形，實現教學的有效突破，從而更好地促進學生的數學學習。

（湖北省武昌水果湖第二小學 ? 430071）