豐富視覺體驗 優化觀察效果

朱宇

《義務教育數學課程標準（2011年版）》中明確指出：“學生應當有足夠的時間和空間經歷觀察、實驗……等活動過程。”數學學習是從感性認識開始的，學生通過以觀察為主要形式的視覺活動對學習素材進行多層面、多角度、多維度的觀察、比較、選擇與歸納，生成視覺體驗。

由此可知，視覺體驗是建立在積極觀察基礎上的歸納與整合，是通過某種特殊的抽象過程而生成的經驗。然而，很多情況下，學生只見表面而不及其里，只關注個別而忽略整體，目之所及卻思維缺席……對此，教師不應簡單歸因為“學生不認真、不細致”，而應該從視覺體驗形成的機理出發，尋找改善學生視覺體驗的具體辦法，提高數學觀察活動的效果。

一、激活視覺意趣

真正的視覺體驗，起步于對物象中形式因素的觀察，發現物象中的疑惑之處或趣味之點。簡單地說，觀察是為了有所發現，隨意進入視網膜里的事物多半與觀察無關。

如在“7的乘法口訣”的鞏固練習環節，教師設計了“比一比，誰的眼力準”的游戲（如圖1）。課件呈現“小豬吹泡泡”的場景，泡泡上雜亂出示7的乘法口訣中的6句，要求學生在短時間里找出少了哪句口訣的得數。

學生聚精會神，仔細觀察，比對口訣，“找到了！找到了！”找到的學生欣喜若狂。隨后，課件又變換出示6個積，讓學生尋找缺少的一個積。游戲進行了4次，學生仍覺意猶未盡。枯燥乏味的口訣背誦變身為興趣盎然的“尋寶游戲”，無需提醒學生“仔細看”， 新穎別致的設計讓學生的視線高度聚焦。

圖1

又如在“找規律”一課的教學時，教師安排了一場比賽：在3秒鐘內迅速記住一長串數字，男生記“162536496481”，女生記“123412341234”。結果，男生組落敗，“不公平”的抗議聲表明，他們對兩組數據進行了觀察比較：第二組數據太有規律了！課尾，教師引導學生再次觀察第一組數據，學生終于參透玄機：“162536496481”的規律是“16，25，36，49，64，81”。原來規律藏在這兒！

在上面的兩個片段中，蘊含數學任務的情境給學生帶來了刺激，他們感受到新奇，思維也發生了沖突，產生一種認知和情感方面的需要，進而產生了屬于自己的真實問題，促使他們主動地觀察，視覺體驗真實地開始了。需要注意的是，如果僅僅是形式上的新奇，只能吸引學生外在的短時興趣。教師既要促進學生外在動機向內在動機的轉化，也要推動學生對情境的外在興趣與數學思維活動的內在興趣緊密結合，從而賦予視覺體驗以“數學”特征。

二、過濾視覺行為

用眼睛看，是容易的，但要透過現象，有所發現是困難的。觀察不僅需要眼睛的凝視，更需要心的凝視。觀察活動的全過程包括初步感受情境，觀察、發現并分析數學問題，每一個環節都會帶給學生不同的體驗、感受和發現。為了確保學生能生成或積累必要的數學觀察經驗，就必須對視覺行為進行有意識的引導與選擇。

例如，在“折線統計圖”的教學中，我們發現，學生在觀察條形和折線兩種統計圖的基礎上，能說出“折線統計圖不但能表示數量的多少，而且能反映數量增減變化的情況”，但是對兩種統計圖各自特點的解讀卻很蒼白，尤其是不清楚怎樣根據數據特點合理選擇呈現方式。

浙江名師俞正強老師在 “折線統計圖”一課教學時采用的方法值得我們借鑒。俞老師先出示“上海月平均氣溫”條形統計圖，學生觀察之后，把能看到的都表達了，可俞老師還在追問：還能看到什么呢？“逼”著學生“過濾”掉其他非本質信息，轉向研究哪兩個月之間溫差比較大，大了幾度，從而體會到折線統計圖產生的合理性和必要性。接著，課件動態演示條形統計圖變化為折線統計圖的過程。審視兩種統計圖，借“主角”這個擬人化的形象，學生感悟到條形統計圖上，1月份一個主角，2月份一個主角，3月份一個主角……12個主角各走1個月，而折線統計圖12個月只有一個主角。舍棄其他非本質信息，聚焦“主角”的“行走軌跡”，學生悟出了根據數據特點合理選擇呈現方式的關鍵——看看有幾個主角。這樣的加工，不僅幫助學生深刻理解了折線統計圖的價值和意義，而且為下一步理解條形統計圖的“離散”和折線統計圖的“聯結”埋下伏筆。

更為常見的是在數學主題圖的觀察環節，如果不引導學生對視覺行為進行過濾取舍，那么豐富的信息資源就容易把學生引入誤區，費時費力。所以，出示主題圖后，教師不妨這樣一問：“同學們，請認真看圖，然后告訴大家你在這幅圖上發現了哪些數學信息？”最后根據學生的回答教師引導歸納，選擇合適問題，讓學生去探究解決。

三、關注視覺理解

經過觀察階段獲得的數學感性經驗，很大程度上僅是一些同某些實物、圖形、操作情境緊密相關的具象，教師還需要據此進行適時適度的抽象，實現感性經驗的提升。

例如，在“長方體的認識”教學中，在發現棱的特征的過程中，教師基于觀察、超越觀察，多次引導學生進行直觀圖形或實踐操作基礎上的觀察活動、想象活動、推理活動，學生在直觀的基礎上不斷產生新的思考。對學生的思考來說，直觀的形式、視角越多樣，積累的表象就越豐富，也就越容易達成數學抽象，越容易實現數學理解。而在接下來探究“面”的特征環節，教師反其道而行之，不再像發現棱的特征那樣先觀察再思考，而是先思考再觀察。

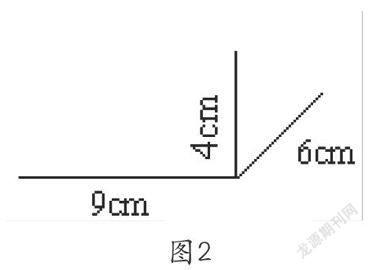
課件先出示一個長方體的長、寬、高（如圖2），接著出示6個圖形（9×9，9×7，9×4，6×6，6×4，4×4），要求學生判別能否從中找到這個長方體的6個面。學生此時觀察到的是長方體“棱”的特征，教師的要求是“從棱聯想到面”，因為有前面實踐活動形成的表象支撐，學生很有條理地說出“因為前面的長是9厘米，寬是4厘米，和9×4的長方形圖是一樣的”。值得一提的是，教師雖然給出了6個圖形，但是其中并沒有上、下兩個面，需要學生去偽存真，在腦海中鑒別、想象、構圖，這進一步拓展了學生的想象空間。推理結束后，教師出示長方體的直觀圖，組織學生共同經歷想象后的驗證活動，概括出長方體面的特征。

再如，在“倍的認識”教學中，課件只出示“12朵黃花”，但卻沒有紅花，只出現一種量，這就讓見慣了“兩種量”的視覺出現了真空。這時，教師提問：我們再來看看，黃花的朵數是紅花的幾倍呢？學生感覺有困難，感嘆“1份紅花有幾朵太關鍵了！”。隨后，教師組織學生“猜一猜”：如果紅花有3朵，黃花的朵數是紅花的幾倍呢？如果1份紅花有4朵、6朵，它們之間的倍數關系又會是怎樣呢？學生先是在紙上圈，漸漸地，教師提出“在自己的腦海里默默地圈一圈”。教師最后的發問畫龍點睛：“孩子們，黃花一直是12朵，那為什么兩種花之間的倍數關系在發生變化呢？”

所謂視覺，是眼中之像經過感知、選擇、分析后形成的某種形式語言的體驗狀態，不只是客觀事物的映像，還包括對事物的假設、推理與理解。所以如以上兩個片段一樣，需要呈現變化的情境，讓視覺擺脫操作性情境的單純刺激，從與活動相當的概念水平上升為抽象理解的水平。

四、完善視覺表達

課堂上，教師還需要組織學生對視覺感知內容進行反思和交流，及時概括所獲得的經驗并進行形式化的表述，使已得經驗條理化和系統化。

還是以“倍的認識”教學為例，教師引導學生將2朵藍花，6朵黃花“圈一圈”，在此基礎上，直觀形成對倍的初步認識：藍花有2朵，黃花有3個2朵，我們就說黃花的朵數是藍花的3倍。接下來，出示藍花2朵，黃花12朵。教師提問：現在黃花的朵數是藍花的幾倍呢？能用圈一圈的方法解決嗎？學生匯報之后，教師設疑：觀察剛才的兩幅圖，你們是怎么一眼就從圖中看出第一幅圖中黃花是藍花的3倍，而第2幅圖中黃花是藍花的6倍的？

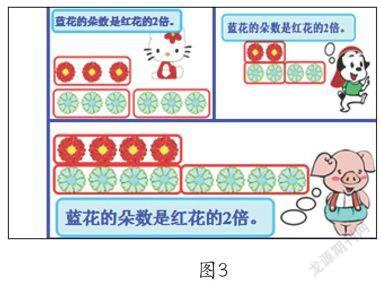
學生由“幾個幾”的實物順利過渡形式化“倍”的概念：能圈出這樣的幾份，就是一份數的幾倍。然而，這樣的視覺注意還只是因教師的提醒而被動地注意，并不是為某種目的尋找特定目標而有指向的選擇。所以，接下來，教師組織學生在比較中充實對倍的認識，掌握倍的內涵。先出示一組圖，都表示“藍花的朵數是紅花的2倍”（如圖3）。組圖的數量變復雜了，學生需要在復雜的環境中找到“特殊”的對象——關于“2倍”背后的共同規律。學生就需要對觀察到的圖意進行類比加工，尋找共性，準確表達。

圖3

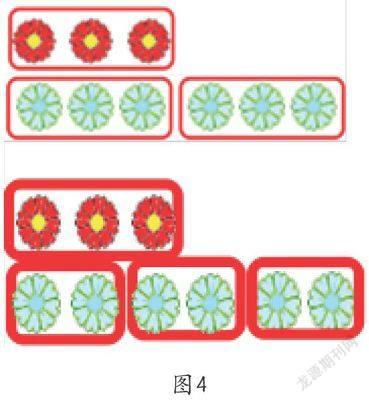
接著，出示圖4，質疑：你覺得下面的哪幅圖能夠表示“藍花的朵數是紅花的幾倍”呢？藍花的朵數是紅花的3倍、還是2倍呢？提供反例為的是讓學生在觀察中比較和思辨，使學生認識到黃花不是隨意圈的，要根據藍花的朵數來圈，從而加深對“倍”的理解，將一般意義上的“看”生成了具有數學特點的視覺語言。

圖4

需要注意的是，不同學生語言表達的能力水平是不一樣的。如果時間倉促，只有少數學生完成了觀察任務，教師就立即組織反饋評價，大多數學生就不能獲得較為充足的觀察體驗。另外，在交流觀察所得的環節，還必須關注學生參與機會的公平性，讓學生暢所欲言，通過互動交流完善觀察體驗。

視覺不只是一種與感覺、知覺有關的生理與心理現象，它其實更是一種特殊的思維方式，與選擇、判斷、整合等智力活動密切相關。課堂上關注學生視覺體驗的完善，有助于學生獲得豐富而深刻的數學活動經驗，學會從數學角度去觀察周圍的世界，讓數學課堂的有效教學真正落到實處。

（江蘇省高郵市天山實驗小學 ? 225600）