淺談初中生數學直覺思維能力的培養
鄧金華
【摘 要】 直覺思維作為人類思維中一種較為重要的思維方式,是現代人才素質必備的思維品質。初中數學教學中要加強對學生進行直覺思維能力的訓練和培養。1.夯實雙基,建立引發直覺思維的契機及智力圖象。2.鼓勵猜測,提高直覺思維的準確性、敏銳性和超常發揮的水平。3.加強數學建模,提供直覺思維突變跳躍的框架和模塊。4.訓練全面思維的方法,提高直覺思維的簡縮能力與突破力度。
【關鍵詞】初中數學;直覺思維;能力;培養
直覺思維,是指對一個問題 未經推理分析,僅依據內因的感知直接地對問題答案作出的覺察和判斷,猜想、設想、突然對問題有“靈感”和長久沉思后的“頓悟”,或者對未來事物發展的結果有“預言”“預感”等都是直覺思維。一個人的數學思維,判斷能力的高低主要取決于直覺思維能力的高低。它是現代人才素質必備的思維品質。因此,我們在初中數學教學中,就要加強對學生進行直覺思維能力的訓練和培養。
一、夯實雙基,建立引發直覺思維的契機及智力圖象
直覺思維并不是憑空臆想、胡亂猜測,“靈機一動”是以人們積累的豐富知識經驗為基礎建立起來的,只有夯實雙基,才能使學生建立以雙基為基礎的智力圖象,引發契機,促進思維從低級的感觀直覺上升到高級的理性直覺。
例1 講授多項式平方后,給出下列趣題:
(1)計算:152=?,252=?,352=?
(2)不計算按規律寫出:852=?,1052=?
學生從152=225,252=625,352=1225中發現個位上的數字是5的兩位數的平方規律,結果是先將十位數字與十位數字加1相乘,再在未尾“添”上25。這一規律可推廣到個位數是5的自然數的平方,即(10n+5)2=100n(n+1)+25,從而852=7225,1952=38025。
直覺思維總是大膽地跳躍到某種結論上,由于結果具有隨機性必須嚴格證明。上述結論可運用多項式平方公式不難證明。
二、鼓勵猜測,提高直覺思維的準確性、敏銳性和超常發揮的水平
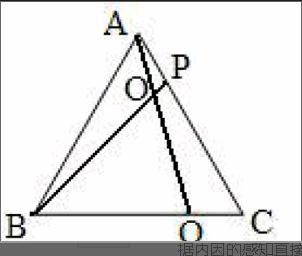
例2 如圖,在等邊⊿ABC的邊AC、BC上各取一點P、Q,使CQ=AP,AQ,BP相交于點O,求∠BOQ的度數。
由于AC、BC邊上的點P、Q是任意的,先讓學生從P、Q分別是邊AC、BC的中點的特殊位置去猜測問題的結果。而這時同樣滿足CQ=AP,并且有了AQ⊥BC,BP⊥AC的條件,又因⊿ABC是等邊三角形,就可以簡單的求出∠BOQ的度數。從而學生可以有目的地去選擇解題的方法。
隨著新課程改革的不斷推進,使圖形變化而結果不變的動態問題在近幾年各地的中考試題中時會出現。我們在平時教學中,教師會用幾何畫板制作動態的教學課件讓學生直觀的理解。然而學生在考試的時候只能憑著一個腦子思考。對于這一類問題就需要學生通過猜想特殊情形的結果,從而合理而正確地尋找和發現一般情形的結果,這樣常常能較快地找到結論。
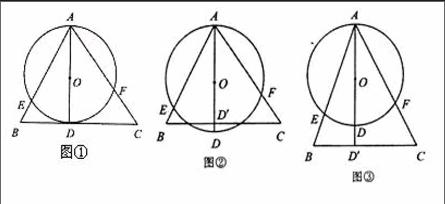
例3 如圖①中,AD是圓O的直徑,BC與圓O相切于點D,AB、AC交圓O于點E、F。
(1)求證:AB·AE=AC·AF;
(2)圖②、圖③分別是將圖①中的直線BC向上平移與圓O相交或向下平移所得,此時,AB·AE=AC·AF是否仍成立?若成立,請證明,若不成立,請說明理由。
在此題中,易見本題的圖①其實是運動中的一個特殊情形。當學生能猜測到這一特殊到一般的思想方法,就不難獲得猜想證明的啟迪。
三、加強數學建模,提供直覺思維突變跳躍的框架和模塊
著名數學家懷特海說:“數學就是對于模式的研究”。布魯納在“教學過程”中指出:“我們的教學與其說是單純地掌握事實和技巧,不如說是教授學習結構。”他指的結構就是學科的基本概念、基本原理、基本方法以及相互聯系所構成的理論框架,只有掌握了學科結構才能有效地掌握學科知識并進行知識能力的遷移。同時,還要善于把已證明過的重要命題轉變為直覺的知識模塊,在以后使用中供“組裝”之用。
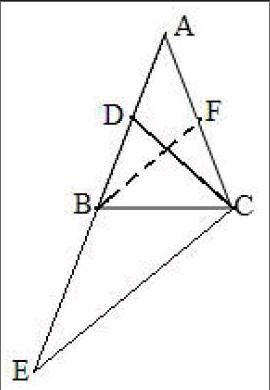
例4 等腰⊿ABC中,CD為腰AB上的中線,延長AB至E,使BE=AB,連結CE,求證:CE=2CD。
學生在遇到2倍關系問題時,憑經驗直覺可構成中位線解題模型,因此添輔助線中線BF,便可迎刃而解。
四、訓練全面思維的方法,提高直覺思維的簡縮能力與突破力度
直覺思維是對思維對象從整體上考察,調動自己的全部知識經驗,通過豐富的想象作出的敏銳而迅速的假設、猜想或判斷,它是一種瞬間思維,省去了一步一步分析推理的中間環節,其邏輯思維的凝結、簡縮、躍進的具體過程往往是不清晰的,是長期積累上的一種升華,是思維過程的高度簡化,是思維者的靈感和頓悟,但是將這些思想環節展開時,可以看到不少是發散思維、類比、歸納和聯想的結果,它清晰地觸及到事物的“本質”。因此教學中要全面介紹形象思維、邏輯思維和直覺思維,使學生能夠從整體上把握問題。
例5 有甲、乙、丙三種貨物,若購甲2件,購乙4件,購丙1件,共需210元;若購甲3件,購乙7件,購丙1件,共需315元。問購甲、乙、丙各一件共需多少元?
容易看到,這是一個方程應用問題,設甲、乙、丙三者單價分別為x元、y元、z元,則
2x+4y+z=2103x+7y+z=315
由于方程組的未知數個數多于方程個數,要解不定方程。如果指導學生把握題目的整體特征,直接求三者單價之和x+y+z,將上述方程轉化為:
(x+3y)+(x+y+z)=2102(x+3y)+(x+y+z)=315
問題就化難為易了。
總之,學生直覺思維能力的培養,不是一朝一夕的事,培養學生的直覺思維能力有很強的科學性創造性,它是一項復雜的系統工程。教師在教學過程中要善于引導學生觀察,及時捕捉直觀信息,有意識有目的地培養學生的直覺思維能力,讓學生的思維在深度、廣度、靈活性、獨立性等方面得到全面發展。
(作者單位:江蘇省常熟市第一中學)

