基于分段分層相似日搜索和自適應脊波神經網絡的風電功率多步預測

張宜陽，嚴歡

（1.國網陜西省電力公司電力科學研究院，陜西 西安 710054；2.國網陜西省電力公司經濟技術研究院，陜西 西安 710065）

基于分段分層相似日搜索和自適應脊波神經網絡的風電功率多步預測

張宜陽1，嚴歡2

（1.國網陜西省電力公司電力科學研究院，陜西 西安 710054；2.國網陜西省電力公司經濟技術研究院，陜西 西安 710065）

隨著大規模風電的并網運行，電網結構越來越復雜，給傳統的電網調度和控制方法帶來了很大的挑戰，而風電功率預測是調度和控制的基礎，如何提高風電輸出功率的預測精度是一個棘手的問題。在實際運行中，提前多步對輸出功率進行準確預測，能夠為電網調度部門實施調度控制、制定運行方式等提供有力支持，有效減輕風電波動對電網的影響，而且可以降低整個系統的運營成本［1］。但是目前對于風電功率的預測主要集中在短期、單步預測上，多步預測的研究較少，且主要是通過滾動迭代預測來實現，即將前一時刻的預測值當做真實值代入網絡輸入端，并去除離當前預測點最遠的歷史數據來預測下一時刻的功率［2］。由于每步的誤差積累，預測的時間不可能很長，且誤差隨超前步數的增加而增大。因此，本文將對風電場輸出功率的短期多步預測展開研究，以期得到更為準確的輸出功率多步預測值。

相似日方法被廣泛應用在短期負荷預測中，且取得了不錯的效果［3-4］。近年來，也有部分學者將相似日的概念引入到風速或風電功率預測中，與負荷預測相比，風電功率預測更具挑戰。

文獻［5］將預測時刻前24 h作為“基準日”，從歷史數據中找出與“基準日”相似的風速時間序列作為徑向基網絡的訓練樣本，對下1 h的即時風速進行預測，沒有真正實現多步預測。文獻［6］采用模式識別技術，以未來日的部分氣象參數作為識別矢量，對歷史日進行搜索，構成訓練樣本集。這些研究都是首先預測風速，再進行風速-功率的轉換，往往帶來較大的誤差。文獻［7］直接對功率進行預測，但僅以日特征向量的相似度來選擇相似日，忽略了實際功率曲線的價值。

盡管文獻［5-7］在選擇相似日時有不同的標準定義，但它的中心思想始終是不變的，即找到能與預測日相似或者對它有慣性作用的歷史日作為訓練樣本來進行建模［8］。而相似日選取的質量好壞也直接影響預測結果的準確度［9］。

基于此，本文將相似日細致到“相似時段”［10］，提出了一種基于相似日理論結合自適應脊波神經網絡的風電功率預測模型。首先在歷史日相應時間段中對基準段實際風電功率曲線的相似曲線進行搜索，并結合風電機組狀態，排除由機組狀態不同而帶來的差異性，強調天氣的影響，進一步保證天氣狀況的趨勢性和連續性；其次，對預測段特征向量進行相似性搜索，采取分層搜索的方法，突出風速和風向作為主導因素的影響；最后，將搜索到的相似樣本輸入自適應脊波神經網絡進行建模、訓練，再用訓練好的網絡進行預測。

1 相似日搜索

傳統相似日方法是通過氣象信息相似度的判定來選擇與預測日變化相似的風電功率序列樣本集，本文提出的基于相似日理論的方法不僅要尋找與預測時刻前12 h變化相似的風電功率曲線，還要尋找與預測時刻后12 h變化相似的日特征向量。

在風電功率預測中，相似日可以是一種廣義上的概念。如圖1所示，以當前12點為界（最新的風電功率數據截止點），將前12 h定義為“基準段”，且風電功率已知；后12 h定義為“預測段”，風電功率未知，待預測。

本文研究的是預測未來12 h的功率數據，即12點至24點的值。“相似日”由兩部分組成：一是0至12點的風電功率曲線與基準段相似；二是12點至24點的氣象參數與預測段相似。

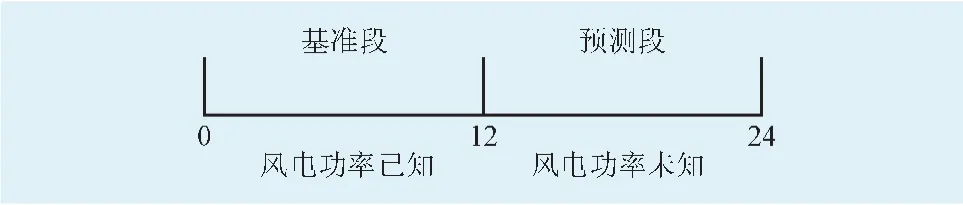
圖1 本文所提相似日的定義Fig.1 Definition of the similar day as proposed in this paper

1.1 基準段相似曲線的搜索

1.1.1 相似曲線的搜索

考慮到計算速度，需縮小選擇范圍，由于風具有日周期和年周期性，在確定歷史日的選擇范圍時，時間不應相隔太久，選擇最近幾個月的數據以及去年同月的某幾天數據構成搜索樣本集。

基準段曲線是各點的輸出功率構成的，在尋找相似曲線時，不僅要形狀相似，還要在功率水平上相似，故同時計算其歐氏距離和相關系數。歐氏距離實質上是表征兩者幾何平均距離的相近性，即功率水平上的相似性。相關系數是一種趨勢的反應，即形狀的相似性。

在實際應用中，2條曲線的歐氏距離小，但相關性可能不大，而歐氏距離大的可能相關性很大。原因在于這是2種不同的標準，從2個不同的角度來描述相似度，必然導致這兩者存在一定的不一致。歐氏距離小的曲線有利于基準段的訓練；而相關系數大的曲線則有助于選擇預測段的相似段，且相關性大的曲線可以通過系數修正來靠近基準曲線，即實現坐標平面的上下平移。歐氏距離和相關系數的計算公式如下。

歐氏距離：

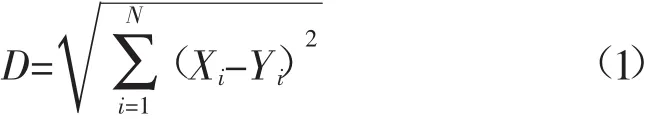
相關系數：

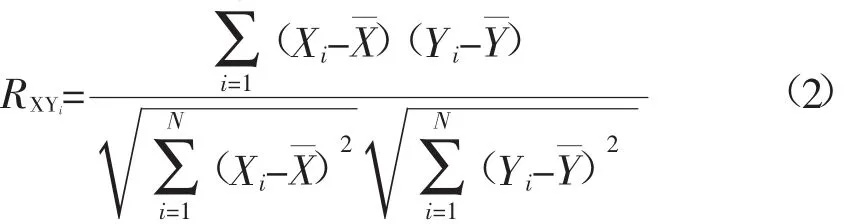
1.1.2 機組狀態的影響

經研究發現，在相近的天氣形勢下有可能出現相似的天氣［5］。由此可以大膽推斷相似的天氣下可能出現相似的風電功率輸出，但是往往會忽略機組狀態的影響，機組的啟停也影響著風電功率的輸出。

如圖2所示，風電功率的輸出由天氣情況、地表情況和機組狀態共同決定。由于同一風電場所處位置不會改變，地表情況對于輸出功率的影響一致，故將其視為不變條件，不予考慮。于是，天氣情況和機組狀態決定了風電功率的輸出。不同的天氣情況和不同的機組狀態可能會有相似的風電功率輸出，換句話說就是功率曲線相似，而天氣情況未必相似，為了最大限度保證天氣趨勢的相似度，本文考慮了機組狀態的影響。

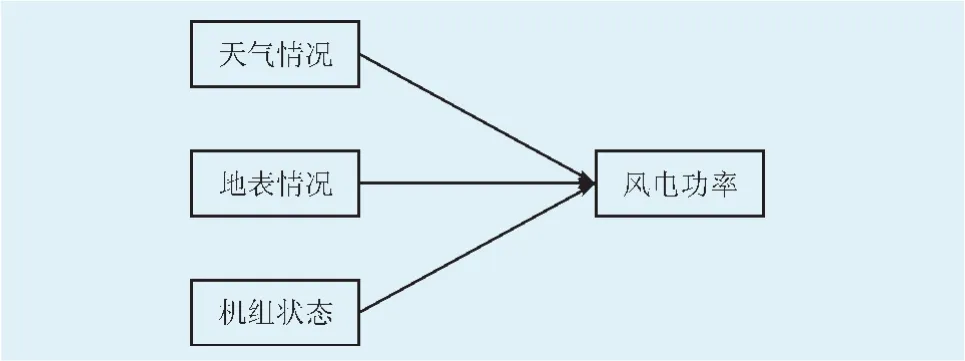
圖2 風電功率的影響因素Fig.2 Effect factors of wind power

氣象因素的影響是一種緩慢的過程，當一種天氣或一種因素發生變化時，功率曲線的變化是平穩且緩慢的，具有相同的變化趨勢［10-11］。倘若基準段的天氣因素與相似曲線的天氣因素相似度比較大，預測段的特征量相似度也普遍比較大。

本文選用4個參數來表征風電機組的狀態，即正常運行、故障停運和計劃檢修的風電機組臺數以及風電機組可用率，分別表示為N、F、J和η。風電機組可用率的計算公式如下。

η=（統計時間-計劃停運時間-非計劃停運時間）/統計時間

其中，

計劃停運時間=計劃檢修維護時間+計劃性技術改造和升級時間+限制風電出力時間

非計劃停運時間=電網故障停機時間+風電機組故障停運時間+環境參數超出許可值的待機時間+風速低于切入風速或高于切出風速的待機時間

設基準段的機組狀態分別為N0、F0、J0和η0，則篩選條件為

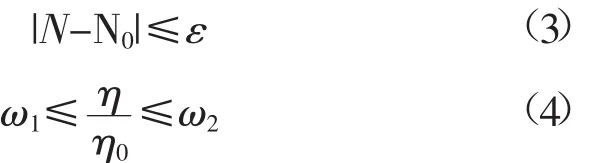
式中，ε∈［0，+∞）一般為一較小正數；ω1∈［0，1）、ω2∈［1，2），且ω1和ω2的取值一般在1左右。具體取值需根據實際情況確定，ε、ω1太大，或者ω2太小會造成篩選效果不明顯，反之又可能導致不能正常地選擇相似段。

1.2 預測段日特征向量搜索

由于功率曲線各點的數據是一個總量參數，即它是不同時刻、不同影響因素的綜合作用的結果，就目前現有的監測系統和信息水平而言，實際上還難以分辨出其中由風速、風向等各氣象因素引起的功率變化分量［8］。但是，風速和風向是主導因素［12-13］，因此，在預測相似段的選取上對主導因素要進行比較精細的處理。

本文對相似段特征向量的搜索采取了分層的方法，即首先搜索相似的風速和風向，且必須保證最大的相似度，在此條件下再對溫度、濕度和氣壓進行搜索。簡單來說就是風速和風向的相似度必須大于某個閾值，而其他條件只要不小于某個閾值就行了。

隨著氣象觀測技術的發展，氣象部門現在能夠獲得越來越精確的氣象數據，與單個統計參數（如日最大、日最小、日平均風速）相比，能更準確、更全面地反映氣象參數在一日內的動態變化過程。

第一層搜索的特征值為風速和風向，構成的特征向量為

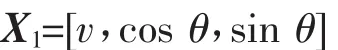
式中，風速向量v=［v1，v2，…，v12］為每小時預報值，cos θ、sin θ分別為主風向的正弦和余弦值。

第二層搜索的特征值為溫度、濕度和氣壓，各影響因素構成的向量為

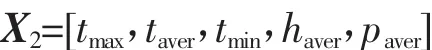
式中，tmax、taver、tmin分別為最高溫度、平均溫度和最低溫度；haver、paver分別為相對濕度百分數和氣壓的平均值。

為了消除不同量綱帶來的影響，采取“極差化”方法對各分量進行歸一化：

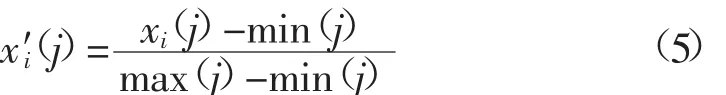
對于日特征向量的搜索，采用計算2個日特征向量之間的夾角余弦來衡量樣本向量之間的差異，具體計算公式為

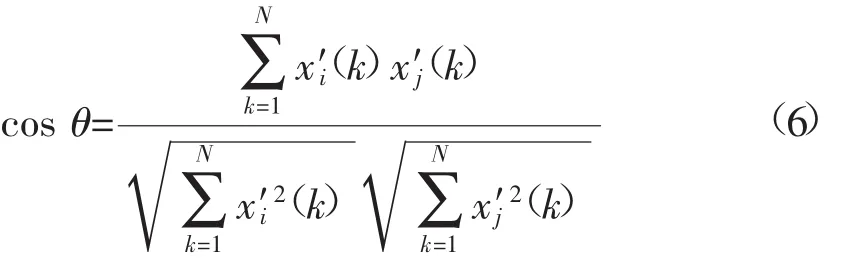
2 自適應脊波神經網絡

逼近多變量函數可以采用基于固定變換的方法和自適應的方法。典型的基于固定變換的逼近方法有傅立葉變換、子波變換等，它們將信號在一組固定的基函數下進行分解，優點是實現方式簡單，缺點是隨著維數的增加它們的計算復雜度劇增，即會出現“維數災難”的問題［14］。神經網絡是一種能夠克服“維數災難”的非參數化函數的自適應逼近方法，理論上，3層前向神經網絡能夠逼近任意一個未知映射。

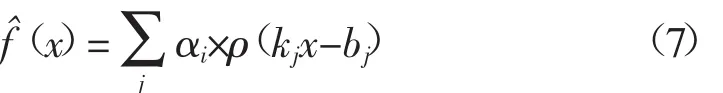
Sigmoid函數的全局特性嚴重違背了大腦神經元的局部激活特性，因此網絡存在著諸如結構復雜、訓練不易收斂、辨識精度較低等缺點。將sigmoid函數用徑向基函數替代形成了徑向基神經網絡，但是它所采用的激勵函數作為網絡隱層單元空間的基函數是存在冗余的，因此它可能會用一個相當冗余的結構來實現一個簡單的映射，從而造成資源的浪費。

另外，將滿足容許性條件的子波函數代替Sigmoid函數作為激活函數，就得到了子波網絡（WNN）的各種模型。在使用子波網絡逼近高維奇異性函數目標函數時，雖然網絡的訓練和學習過程能補償奇異性所帶來的失真，但子波本身處理高維非點狀奇異性的“失敗”，使得子波函數逼近這類目標函數的結果表現出了奇異性擴散的跡象；和其他神經網絡一樣，子波網絡對高維樣本的處理能力缺乏有效的方法，在高維時也需要大量增加節點的數目，從而增加了網絡的復雜度［16］。因此，選擇能表征空間幾何信息的方向基函數作為神經元的激勵函數，將能更有效地處理高維信息，同時和生物神經系統更為一致。

脊波網絡就是這樣一種多尺度幾何網絡，使用脊函數作為神經元激勵函數的脊波網絡模型是一種既能像傳統神經網絡那樣表示階梯函數，在高維空間中又具有子波網絡在一維時的效果的自適應網絡。它同時具有脊函數可調以及神經網絡的并行學習等優點，可以對高維函數和某些具有空間不均勻性的函數進行有效的逼近。

若函數f（x）：Rd→Rm滿足

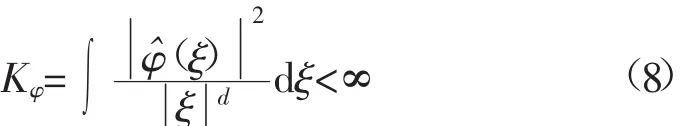
其中，參數γ=（a，u，b）（分別表示脊波的尺度、方向和位置）屬于神經元參數空間Γ=｛γ=（a，u，b），a，b∈R，a＞0，u∈Sd-1，‖u‖=1｝Sd-1為d維空間的單位球面。

對于任何多變量函數f∈L1∩L2（Rd），均可以展開為脊函數疊加的形式：

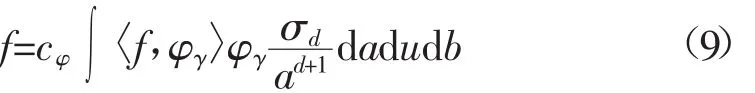
式中，cφ=π（2π）-dK-1φ；σd是維數為d的空間中單位球Sd-1的表面積。

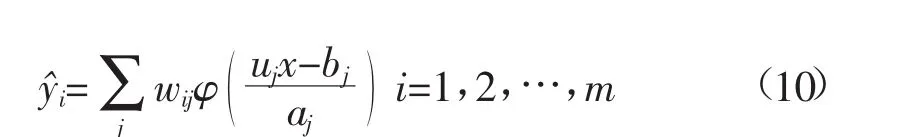
對于輸出為m維的函數f（x）：Rd→Rm來說，均可以分解為m個Rd→R的映射，選擇脊波函數作為基變量，從而有如下使用脊波函數的逼近方程：式中，x、uj∈Rd，‖uj‖=1，Y?=［y?1，…，y?m］，wij表示脊函數的疊加系數。將脊波函數作為一個3層前向網絡的隱層神經元的激勵函數，就可以得到如圖3所示的自適應脊波網絡的結構。

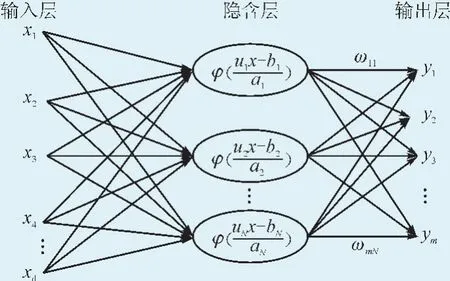
圖3 自適應脊波神經網絡模型Fig.3 Model of self-adaptive ridgelet neural network

設共有P個學習樣本，X=［X1，…，XP］，Y=［Y1，…，YP］，其中XP=［x1t，…，xdt］，YP=［y1t，…，ydt］，t=1，…，P，Zj=［zj1，…，zjp］，j=1，…，N，為第j個隱層神經元的輸出，則對于第t個輸入樣本，網絡的第j個隱層單元的輸出可以寫作：

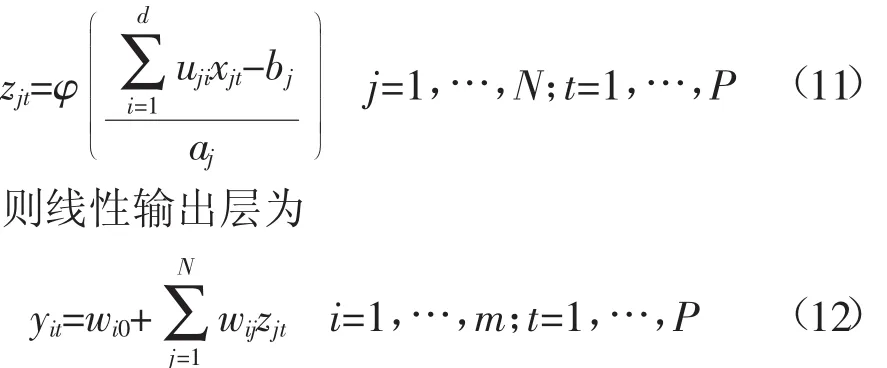
從自適應脊波網絡的整個計算過程來看，網絡的訓練實際上是基于訓練數據，用自適應的方法尋找一族合適的脊波函數和相應的脊波系數，從而實現對輸入輸出映射的最佳重構［17］。

3 相似日理論結合脊波神經網絡風電功率預測

3.1 預測步驟

文獻［2］說明當充分考慮歷史功率、風速和風向等影響因素時，直接預測的效果要好于間接預測，因為間接預測的每一步都會有預測誤差和計算誤差，積累的誤差較大。本文綜合考慮了歷史功率和氣象信息的影響，故采取直接預測功率的方法。預測程序大致分為2部分：一是“相似日”的搜索；二是脊波網絡的訓練、預測。具體步驟如下。

1）在最近幾個月的歷史日中（有條件的可以增加前幾年同月份某幾日的數據）提取對應時間的功率曲線，搜索與基準曲線相似度最高的10條曲線。

2）以基準曲線的值作為輸出，其相似曲線的值作為輸入，建立自適應脊波神經網絡，并進行訓練。

3）查看基準曲線和10條相似曲線當日的風電機組狀態表，舍棄偏移過大的。

4）相似曲線的后12 h即為預測段的潛在相似時段，通過計算日特征向量的相似度進行篩選，最終確定預測段的相似時段。

5）將預測段的相似時段的功率值作為輸入，用訓練好的網絡進行預測，最終得預測段的功率值。

圖4為相應的預測流程圖。

3.2 算例分析

以某風電場為例進行驗證，該風電場共安裝78臺機組，單機容量為850 kW，總裝機容量為66.3 MW。以2011年3、4月及其相似數據為訓練樣本，對2011年5月31日12時至24時的風電輸出功率進行預測，樣本采樣間隔為5 min。每個歷史段的相似段個數選為3。

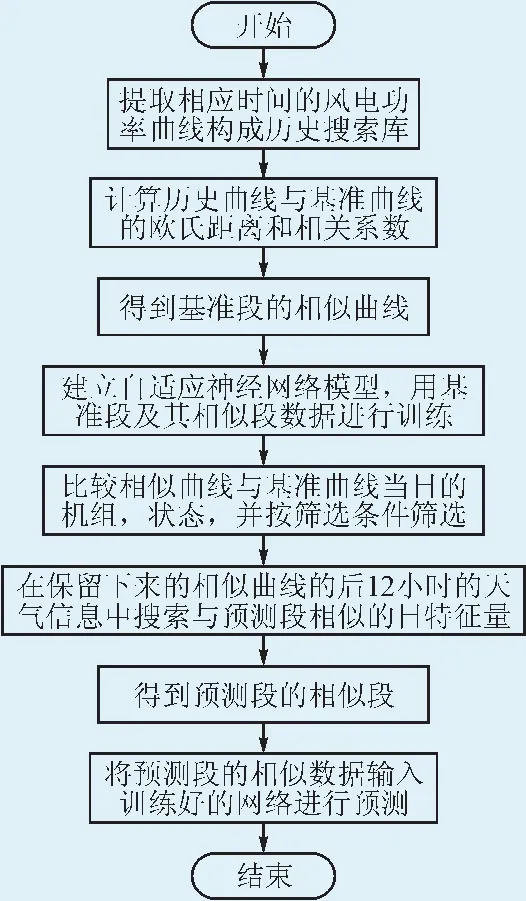
圖4 預測流程圖Fig.4 Forecasting flow chart

歐氏距離和相關系數的計算結果如表1所示，表1中分別列出了在2種標準下最佳的前10個相似日時段，可以看出，除了第20日和27日（00：00-12：00）的結果較好外，其他都出現了矛盾。為此，分別取二者的前5位進行處理。

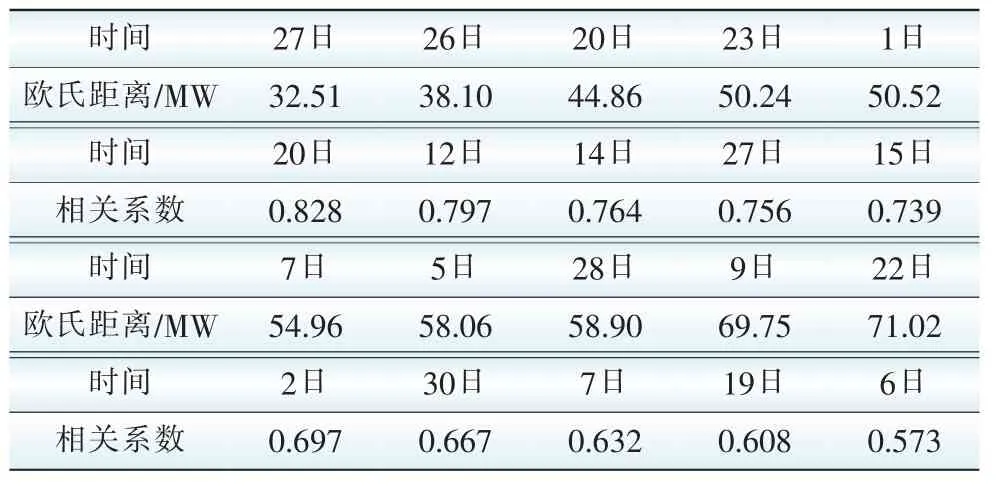
表1 歐氏距離和相關系數計算結果Tab.1 Results of Euclidean distance andcorrelation coefficient

如圖5所示分別是歐式距離最小、相關系數最大的5條曲線與基準曲線的對比，可以看出，歐氏距離小的曲線靠得很近，但規律性不強；而相關系數大的曲線表現出了很強的規律性，這也說明功率水平上的相似和形狀趨勢上的相似不一致，分開計算、分析有一定的意義。

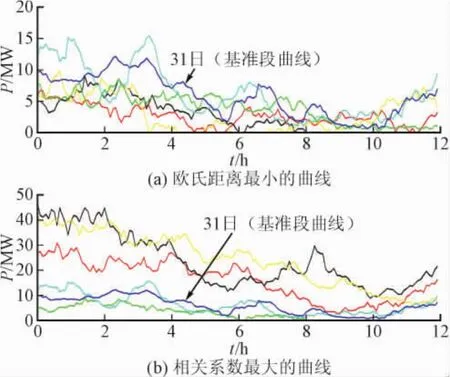
圖5 歐式距離最小的5條曲線和相關系數最大的5條曲線Fig.5 Curves of the five least Euclidean distances and the five maxima correlation coefficient

從圖5可以看出，12、14和15日的曲線相關系數大，但在空間上的距離卻很遠，但是經過一定的系數修正，可以實現坐標平面的上下平移，從而在保證相關性大的基礎上接近基準曲線，如圖6所示。

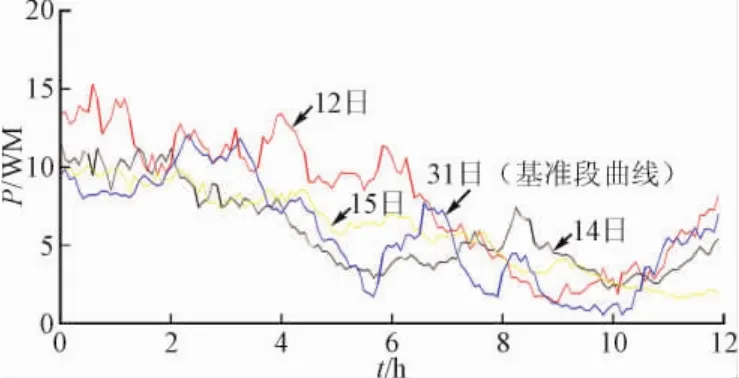
圖6 經系數修正后的曲線Fig.6 Curves revised by ratio

初步將這10條曲線作為相似曲線，將各曲線當時的機組狀態與基準曲線的機組狀態進行對比，如表2所示。取ε=2，ω1=0.95，ω2=1.05，由結果可看出，這幾天均未出現因故障或檢修停運的機組，但是1、20和23日的機組可用率與基準段的差異過大（η＜0.95），被篩選掉。

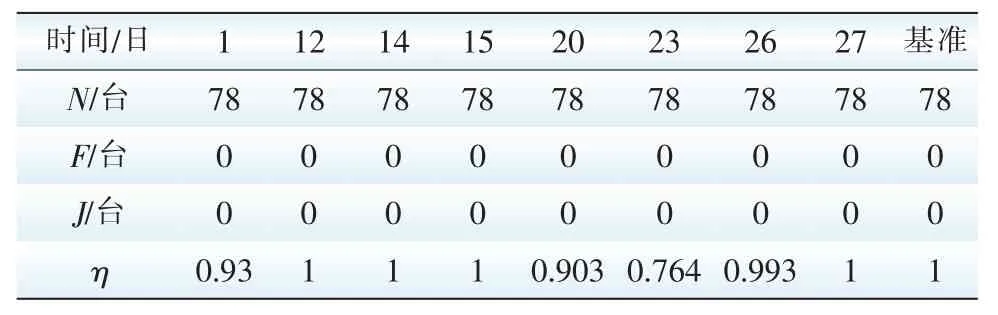
表2 風電機組狀態Tab.2 State of wind turbines

剩下12、14、15、26和27日的相似段的后12 h為預測段的潛在相似段，計算其日特征向量的夾角余弦值，并將結果列于表3中。

最終，得到預測段的相似段為12日、26日和27日的12：00-24：00的功率時間序列。用自適應脊波神經網絡進行建模，模型為網絡結構，3為輸入層，8為隱含層，1為輸出層，得到的預測結果如圖7所示。

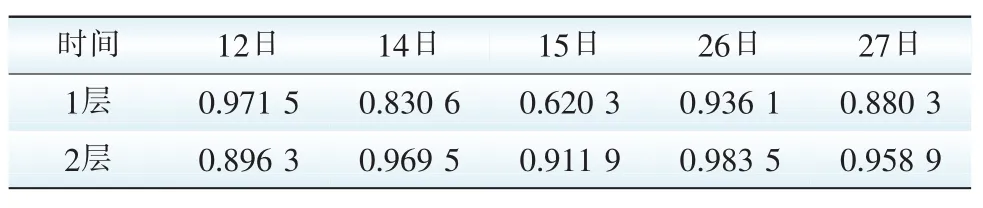
表3 日特征向量相似度計算結果Tab.3 Calculation results of similarity degree of daily feature vector

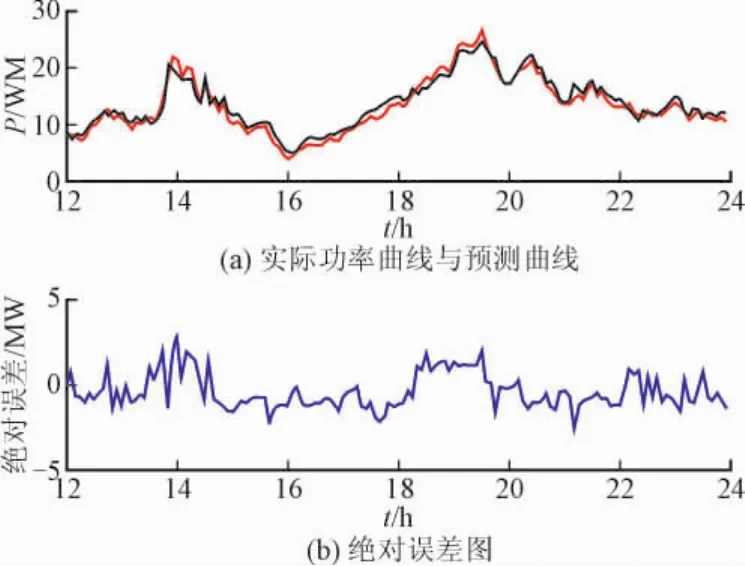
圖7 預測結果Fig.7 Forecasting results

圖8列出了預測值與真實值的散點圖，可以看出，預測值與真實值呈線性關系，且擬合較好，說明該預測結果能較好地反映真實情況。進一步對誤差進行統計分析，得到誤差分布圖，如圖9所示，97%的誤差都在±0.03 pu之間，預測結果較穩定。

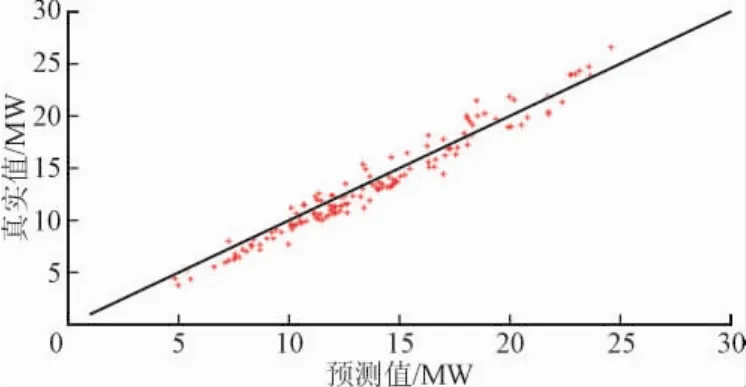
圖8 預測結果散點圖Fig.8 Scatter plot of forecasting results

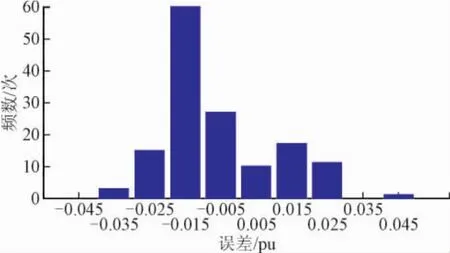
圖9 預測誤差統計Fig.9 Statistic of forecasting errors

為了說明本文所提模型的有效性，將3種模型的結果進行對比。

模型1：本文所提模型。

模型2：基于相似日理論選擇相似樣本，采用BP神經網絡模型進行風電功率預測。

模型3：采用傳統相似日方法，即只用日特征向量搜索相似日，并采用脊波神經網絡模型進行預測。

表4中分別對應的是平均百分比誤差、均方根誤差，計算公式為

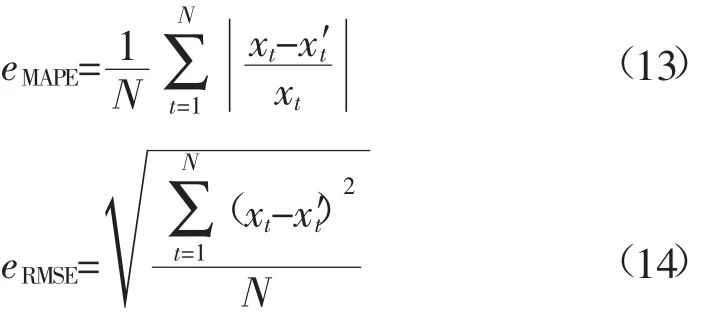
式中，xt為實測值；x′t為預測值；N為預測值的個數。

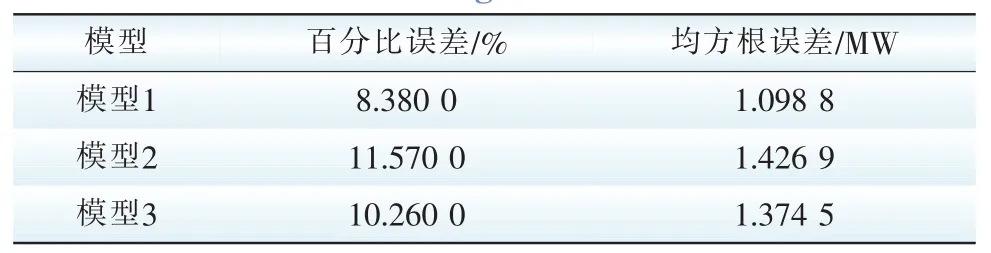
表4 各模型預測誤差Tab.4 Forecasting errors of all models

4 結論

1）基于相似日理論，本文在基準段曲線相似度的基礎上結合機組啟停狀態，并引入了預測段的特征量，增加了相似日的評估信息，使得相似日的選取更加合理、準確。

2）在搜索相似信息時采用了雙重分層搜索，雙重搜索保證了相似精度，分層搜索突出了主導因素，梯次逼近搜索目標，既滿足了精度，又縮小了搜索范圍，提高了計算速度。

3）自適應脊波神經網絡具備了神經網絡所特有的分布式存儲、并行式處理、自適應性、強容錯性和魯棒性等特點，使用脊函數作為神經元激勵函數又有效地解決了傳統神經網絡處理高維信息時的一些缺點，因此適合風電功率的預測。

4）通過本文所提方法進行相似信息的搜索，篩選出了一些與預測段相似的或者有慣性作用的訓練樣本進行建模，由于訓練樣本集對預測模型外推能力影響較大，經算例分析表明，該方法能有效提高預測精度。

［1］劉永前，韓爽，胡永生.風電場出力短期預報研究綜述［J］.現代電力，2007，24（90）：6-11.

LIU Yongqian，HAN Shuang，HU Yongsheng.Review on short-termwindpowerprediction［J］.ModernElectric Power，2007，24（90）：6-11（in Chinese）.

［2］茆美琴，周松林，蘇建徽.基于脊波神經網絡的短期風電功率預測［J］.電力系統自動化，2011，35（7）：70-74.

MAO Meiqin，ZHOU Songlin，SU Jianhui.Short-term wind power forecast based on ridgelet neural network［J］. Automation of Electric Power Systems，2011，35（7）：70-74（in Chinese）.

［3］康重慶，程旭，夏清，等.一種規范化的處理相關因素的短期負荷預測新策略［J］.電力系統自動化，1999，23（18）：32-35.

KANG Chongqing，CHENG Xu，XIA Qing，et al.A new unified approach to short-term load forecasting considering correlated factors［J］.Automation of Electric Power Systems，1999，23（18）：32-35（in Chinese）.

［4］黎燦兵，李曉輝，趙瑞，等.電力短期負荷預測相似日選取算法［J］.電力系統自動化，2008，32（9）：69-71.

LI Canbing，LI Xiaohui，ZHAO Rui，et al.Power load forecasting similar days selecting algorithm［J］.Auto-mation ofElectricPowerSystems，2008，32（9）：69-71（in Chinese）.

［5］鄭婷婷，王海霞，呂泉，等.基于相似日選取樣本的短期風電功率混沌預測［J］.電網與清潔能源，2013，29（3）：74-79.

ZHENG Tingting，WANG Haixia，Lü Quan，et al.Shortterm wind power forecasting based on trend-similar days and chaotic time series［J］.Power System and Clean Energy，2013，29（3）：74-79（in Chinese）.

［6］吳興華，周暉，黃梅.基于模式識別的風電場風速和發電功率預測［J］.繼電器，2008，36（1）：27-32.

WU Xinghua，ZHOU Hui，HUANG Mei.Wind speed and generated power forecasting based on pattern recognition in wind farm［J］.Relay，2008，36（1）：27-32（in Chinese）.

［7］孟洋洋，盧繼平，孫華利，等.基于相似日和人工神經網絡的風電功率短期預測［J］.電網技術，2010，34（12）：163-167.

MENG Yangyang，LU Jiping，SUN Huali，et al.Shortterm wind power forecasting based on similar days and artificial neural network［J］.Power System Technology，2010，34（12）：163-167（in Chinese）.

［8］周暉，王瑋，秦海超，等.基于多時段氣象數據判斷相似日的日負荷曲線預測研究［J］.繼電器，2005，33（23）：41-45.

ZHOU Hui，WANG Wei，QIN Haichao，et al.Study of next-day load curve prediction based on similar days determ ined by daily multi-intervals meteorological data［J］.Realy，2005，33（23）：41-45（in Chinese）.

［9］鞠平，姜巍，趙夏陽，等.96點短期負荷預測方法及其應用［J］.電力系統自動化，2001，25（22）：32-36.

JU Ping，JIANG Wei，ZHAO Xiayang，et al.Ninety-six points short-term load forecasting—theory and applications［J］.Automation of Electric Power Systems，2001，25（22）：32-36（in Chinese）.

［10］楊正瓴，田勇，張廣濤，等.相似日短期負荷預測的非線性理論基礎與改進［J］.電網技術，2006，30（6）：63-66.

YANG Zhengling，TIAN Yong，ZHANG Guangtao，et al.Nonlinear theoretical foundation and improvement of similar days method for short term load forecasting［J］.Power System Technology，2006，30（6）：63-66（in Chinese）.

［11］張芳明，李俊周，毛弋.基于相似日權重的電力系統擴展短期負荷預測［J］.電力系統保護與控制，2009，37（20）：69-73.

ZHANG Fangming，LI Junzhou，MAO Yi.Extended shortterm load forecasting based on similar days weight［J］.Power System Protection and Control，2009，37（20）：69-73（in Chinese）.

［12］范高鋒，王偉勝，劉純，等.基于人工神經網絡的風電功率預測［J］.中國電機工程學報，2008，28（34）：118-123.

FAN Gaofeng，WANG Weisheng，LIU Chun，et al.Wind power prediction based on artificial neural network［J］.Proceedings of the CSEE，2008，28（34）：118-123（in Chinese）.

［13］李德超.一種基于BP神經網絡的快速諧波分析算法研究［J］.電瓷避雷器，2014（6）：67-71.

LI Dechao.Study of fast harmonic analysis algorithm based on BP neural network［J］.Insulators and Surge Arresters，2014（6）：67-71（in Chinese）.

［14］焦李成.自適應多尺度幾何網絡理論與應用［M］.西安：西安電子科技大學，2005.

［15］BARRON A R.Universal approximation bounds for superpositions of a sigmoidal function［J］.IEEE Trans. Inform.Theory，1993（39）：930-945.

［16］焦李成，楊淑媛.自適應多尺度網絡理論與應用［M］.北京：科學出版社，2008.

［17］孫鋒利，何明一，高全華.基于自適應脊波網絡的高光譜遙感圖像分類［J］.計算機科學，2011，38（8）：260-264.

SUN Fengli，HE Mingyi，GAO Quanhua.Hyperspectral image classification based on adaptive ridgelet neural network［J］.Computer Science，2011，38（8）：260-264（in Chinese）.

（編輯 董小兵）

Multi-Step Wind Power Forecasting Based on Subsection and Layer Searching for Similar Day and Adaptive Ridgelet Neural Network

ZHANG Yiyang1，YAN Huan2
（1.Shaanxi Electric Power Research Institute，Stae Grid Shaanxi Electric Power Company，Xi’an 710054，Shaanxi，China；2.State Grid Shaanxi Electric Power Corporation Economic Research Institute，Xi’an 710065，Shaanxi，China）

為進一步提高風電功率預測精度，提出了一種基于相似日理論結合自適應脊波神經網絡的風電功率預測模型。在傳統相似日方法上，將相似日細致到“相似時段”，即基準段和預測段；采取對基準段風電功率曲線和預測段日特征向量進行雙重搜索的方法，保證了相似精度；并采用分層搜索逐步逼近預期目標，既突出主導因素又節約計算時間。在基準段曲線相似度的基礎上結合機組啟停狀態，并引入了預測段的特征量，增加了相似日的評估信息，使得相似日的選取更加合理、準確。用自適應脊波神經網絡對相似樣本進行建模、訓練，得最終預測值。經算例分析，該方法能有效預測未來12 h的風電輸出功率，從而實現較高精度的多步預測，為調度部門提供有力支持。

風力發電；相似日；功率預測；脊波網絡；多步預測

To further improve the wind power prediction accuracy，this paper introduces a wind power forecasting model based on the similar day theory and adaptive ridgelet neural network.On the basis of the traditional similar day method，the similar day is further divided to the“similar period”，that is，the reference period and forecasting period.To guarantee the similar accuracy，wind power curves in the reference period and daily feature vector in the forecasting period are both searched. To highlight the main factors and save calculating time，the hierarchical search is used to gradually approach the anticipated goal.Assessment information of similar days is increased by introducing the state of wind turbines and characteristic quantity in the forecasting period on the basis of similarity of the reference curve.Therefore it is more reasonable and precise to select similar days.In the end，similar data are inputted in the adaptive ridgelet neural network for modeling，training and forecasting.The analysis results show that the method proposed in this paper can effectively forecast wind power in the next 12 hours，and achieve relatively high multi-step accuracy，thus it can offer convincing supports the power dispatch department.

wind power generation；similar day；power forecasting；ridgelet network；multi-step forecasting

1674-3814（2015）04-0124-08

TM71

A

2014-08-18。

張宜陽（1986—），男，碩士，工程師，研究方向為電力系統自動化。