同軸結構半徑突變處補償電容的計算分析

焦重慶 李明洋

（新能源電力系統國家重點實驗室（華北電力大學）北京 102206）

0 引言

在電力測試線、GIS 套管、微波傳輸和耦合電路等同軸結構中，常會出現導體半徑的突變。半徑的突變會激發起高階電磁模式[1]。在單模工作狀態下，這些高階模式主要分布在突變處附近，沿兩側會呈指數衰減。文獻[2-4]基于全波的方法分析得出，高頻時，在半徑突變處兩邊的外導體上電位連續、電流不連續。在某些實際情況中，比如GIS 的開關操作，同軸導體外徑在半米以內，而最高感興趣的頻率一般不超過100MHz[5-7]，此時波長遠大于同軸結構的外徑。半徑突變對橫向電磁場（Transverse Electric and Magnetic Field，TEM）模傳播的影響可等效為一個位于半徑突變處的集總補償電容[4]。

文獻[4]基于全波的方法，可以考慮補償電容的頻變效應，推導過程和計算公式均較復雜；對于本文尺寸，參照文獻[4]的計算，靜態補償電容與100MHz 時的補償電容的相對誤差不超過5%，在工程應用允許的誤差范圍內，即可以忽略補償電容的頻變效應，用靜態電容代替。本文利用分離變量法，基于同軸結構半徑突變處電位分布的精確計算，推導了靜態補償電容的精確計算模型。該計算模型計算簡單，便于工程應用。

1 計算模型

同軸結構的半徑突變模型如圖1 所示。半徑突變處位于區域A、B 的分界面oo'上，假設突變處兩邊的同軸線均勻且無限延伸。取同軸線的軸向為z向，z 軸的坐標原點在半徑突變處的分界面上，z 軸的正方向由區域A 指向區域B。內導體的半徑為r1，區域A 外導體的內半徑為r2，區域B 外導體的內半徑為r3。內導體施加電壓U0，外導體電位為0。

圖1 同軸結構半徑突變模型Fig.1 Model of abrupt change of radius in coaxial structure

圖1 所示結構的電路模型可由特征阻抗分別為Z0A、Z0B，傳播常數分別為γ0A、γ0B的傳輸線和表征半徑突變效應的補償電容Cc來等效，如圖2 所示。

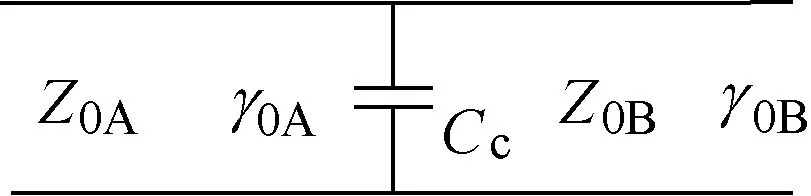
圖2 半徑突變的同軸結構的等效電路Fig.2 Equivalent circuit of a coaxial structure with abrupt change of radius

先利用分離變量法[8]解出區域A、B 的電位分布，再由導體上的電荷分布及內外導體間的電壓求出補償電容Cc的值。

區域A 的電位分布表達式為

式中，J0、Y0分別為第一、第二類貝塞爾函數；U0為內外導體間的電壓（V）；式（1）等號右邊的第一項表示均勻同軸線內的電位分布。φA1是利用分離變量法解得的圓柱坐標系中拉普拉斯方程的一般解[9]，φA1表示由于半徑突變的存在引起的電位分布的畸變，并且 φA1在區域A 中的內外導體表面邊界上滿足條件

將式（3）、式（4）分別代入式（2），可得

求解由式（5）、式（6）組成的方程組，若En、Fn有非0 解，必有系數行列式為0，如式（7）所示。

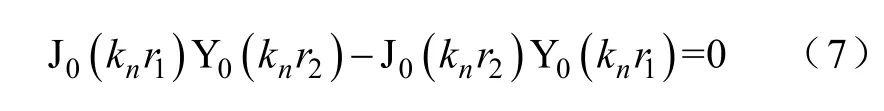
求解式（7），得kn為一系列正數[10]。

由式（5）可得

將式（8）代入式（2），并定義

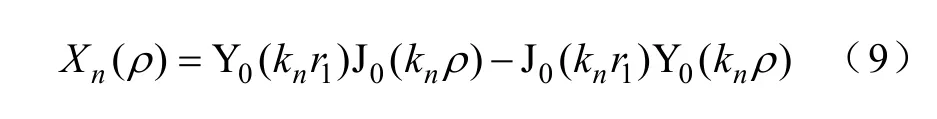
則式（2）可表示為

式（10）、式（15）中的未知系數An、Bm可利用區域A、B 分界面上的邊界條件[11]確定，邊界條件為

由式（12）、式（13）可以證明，當n ≠i 時，式（22）中等號左邊的項的積分為0，則式（22）可以簡化為

式（23）表明系數iA 可以用系數Bm表示，即

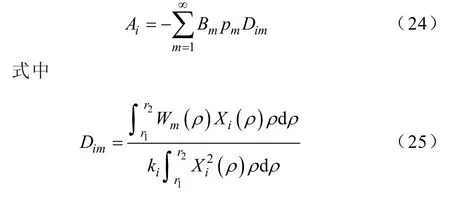
在z=0，r1＜ ρ＜r3邊界上，由式（19）、式（20）可得

將式（1）、式（14）代入式（26），并利用正交性得

將式（24）代入式（27），整理式（27）可得關于Bm的線性方程

對j、m 分別從1 取到M，且m≠j，就構成了由M 個方程組成的方程組，并可解出系數Bm的值，進而由式（24）解出nA 的值。

補償電容的值僅與結構突變處高階模式的電位引起的電荷分布有關，即僅需考慮由 φA1和 φB1引起的導體上的電荷分布。

區域A 內由 φA1引起的內導體表面的電荷密度分布為

區域A 內由 φA1引起的內導體表面總電荷量為

同理，區域B 內由 φB1引起的內導體表面的總電荷量為

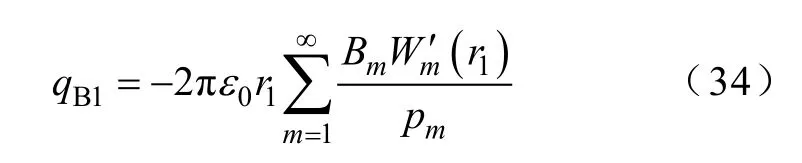
則由尺寸突變引起的該同軸結構的補償電容為

2 對比驗證及規律分析

以變分原理為基礎建立的有限元法[13]已被普遍推廣并成功應用于電磁場工程問題等應用技術領域。本文利用Ansys 和Maxwell 兩種有限元軟件計算驗證了上述公式的正確性。有限元計算模型如圖3 所示。利用同軸結構的軸對稱特性，畫出二維軸面；模型的總長度L 遠大于區域B 的外導體半徑r3。在模型的左、右邊界分別施加電場平行邊界條件；內導體施加1V 電壓，外導體電位為0。

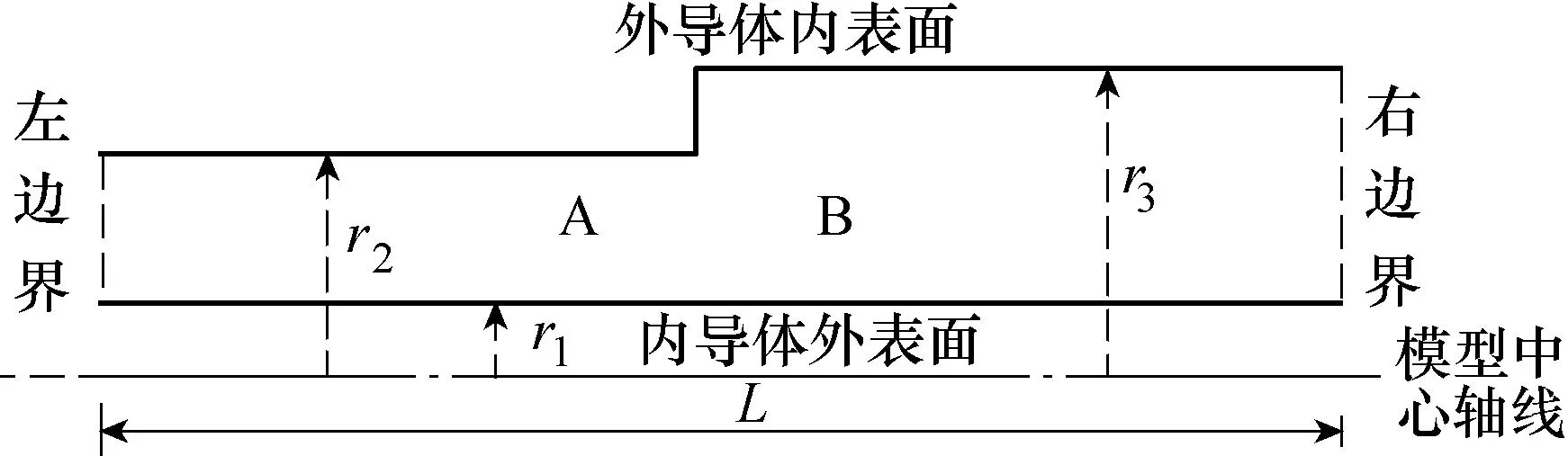
圖3 補償電容的有限元計算模型Fig.3 Model in FEM for calculating the compensation capacitance

本文分別對比了“z=0，r1＜ρ＜r2線上的電位分布”和“內導體表面電場強度”，以驗證本文公式在不同點上的計算結果與有限元結果一致，如圖4、圖5 所示。其中，計算模型的尺寸為r1=0.1m、r2=0.2m、r3=0.3m。由圖4、圖5 可見，圖中的公式計算結果與有限元軟件的計算結果的一致性很好，說明本文公式的正確性。

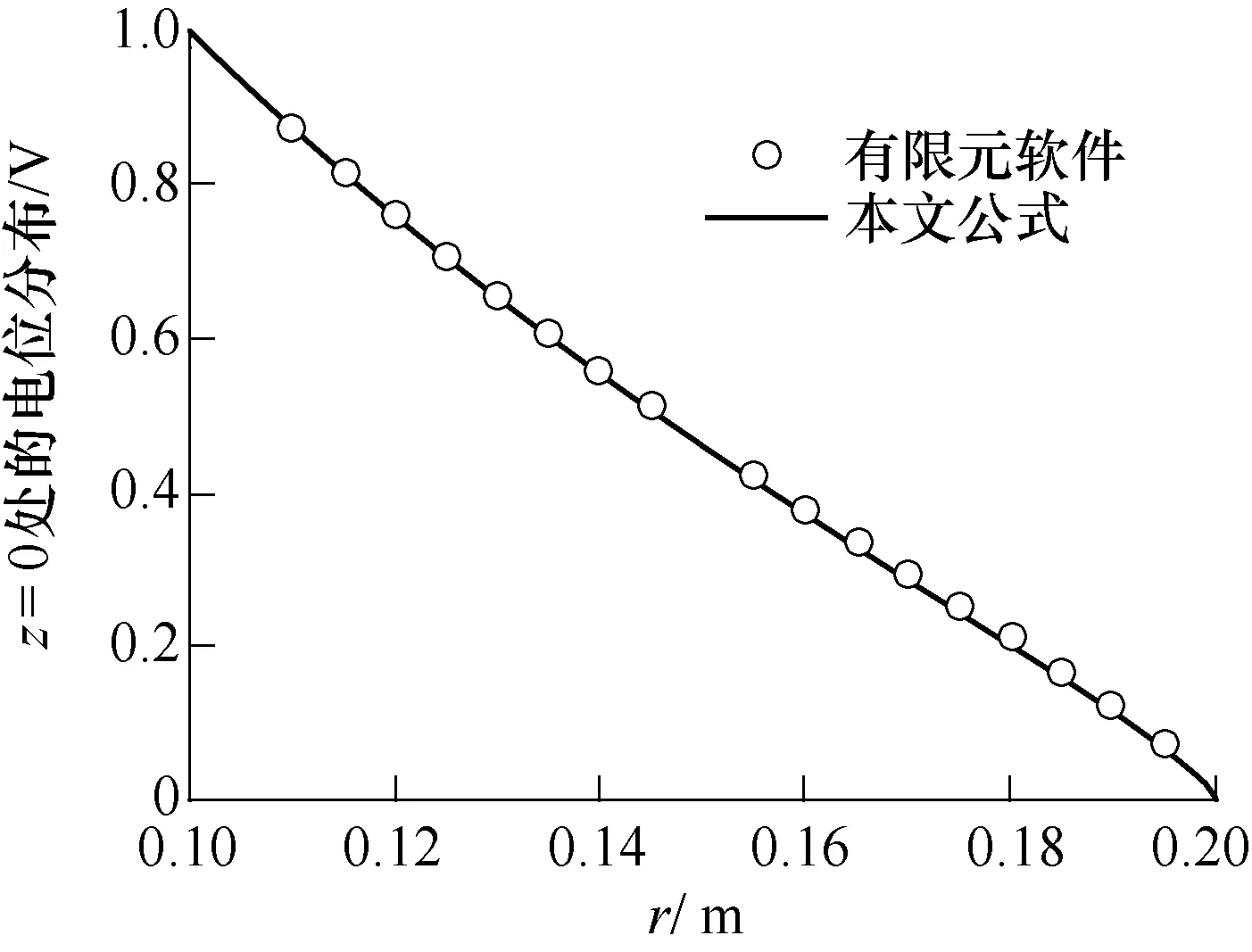
圖4 z=0，r1＜ρ＜r2線上的電位分布的對比Fig.4 Comparison of potential distribution at z=0,r1＜ρ＜r2

圖5 內導體表面電場強度的對比Fig.5 Comparison of electric field intensity at inner conductor surface

有限元計算模型的補償電容Cd為

式中，Ctotal為內外導體間的總電容；CA、CB分別為均勻區域A、B 段的電容，利用區域A、B 的同軸結構單位長電容公式乘以長度計算。

文獻[5]基于Schwarz-Christoffel（施瓦茲-克里斯多菲）變換[14]，給出了平行平板結構的尺寸突變處的橫向單位長度靜態補償電容的精確計算公式

由式（37）乘以同軸結構內導體周長可近似應用于同軸結構半徑突變處補償電容的計算，即

圖6 和圖7 給出了不同半徑取值下補償電容的四種計算方法的對比結果。由圖6 和圖7 可見，本文計算模型與有限元軟件的計算結果相對誤差較小。近似公式與有限元軟件的相對誤差較大；且r2/r1越小，r3/r1越大，補償電容的值越大。

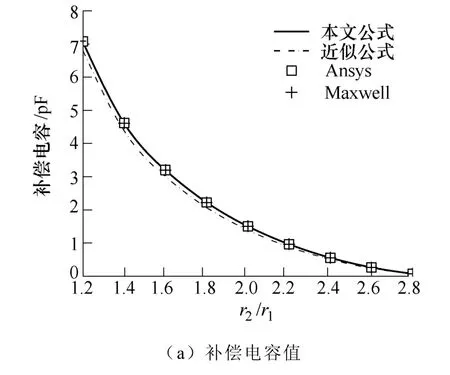
圖6 r1=0.1m，r3=0.3m，不同r2/r1時補償電容的對比Fig.6 Comparison of compensation capacitance value among different r2/r1with r1=0.1m and r3=0.3m

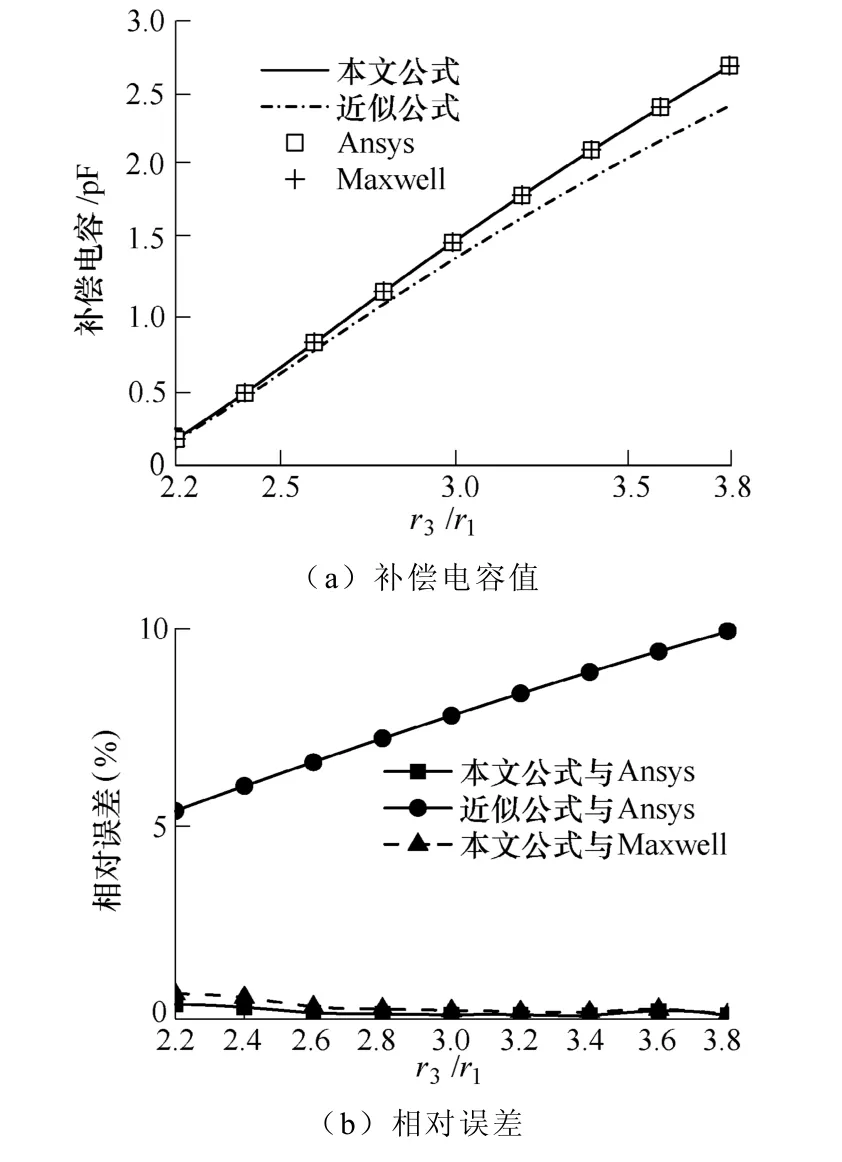
圖7 r1=0.1m，r2=0.2m，不同r3/r1時補償電容的對比Fig.7 Comparison of compensation capacitance value among different r3/r1with r1=0.1m and r2=0.2m

3 應用算例

為分析補償電容對時域信號傳輸的影響，作了“有補償電容”和“忽略補償電容”時半徑突變的同軸結構的終端電壓的對比。基于EMTP[15,16]仿真平臺的仿真模型如圖8 所示。其中，計算模型的尺寸為r1=0.1m，r2=0.2m，r3=0.3m，區域A、B 的同軸線的長度均為1m。在區域B 的始端加上升時間為5ns、下降時間為50ns、幅值為10kV 的雙指數函數信號源，仿真的時間步長為0.005ns。區域A 的終端接不同負載R，對比區域A 終端的電壓。

圖8 EMTP 仿真模型Fig.8 Simulation model using EMTP

區域A 終端電壓的對比結果如圖9 所示。由圖9 可見，當區域A 終端接匹配電阻時，臺階電容對時域信號的傳輸影響很小。當區域A 終端接1MΩ或0.1Ω電阻時，由于阻抗不匹配產生了信號的折反射，由圖9b、圖9c 可見，在多次折反射后，忽略補償電容時的電壓波形比有補償電容時的電壓波形超前。

圖9 補償電容對時域信號傳輸的影響Fig.9 Comparison of influence of compensation capacitance to transmission of the time domain signal

4 結論

本文推導出同軸結構半徑突變處靜態補償電容的精確計算模型，該模型計算簡便，準確度高，計算結果與有限元軟件的結果的相對誤差不超過1%，也說明了本文計算模型的正確性；并且當負載不匹配時，相比考慮半徑突變同軸結構等效電路的補償電容時，忽略補償電容時會產生信號超前。平行平板結構尺寸突變處靜態補償電容的精確公式近似應用于同軸結構時誤差較大，在一些尺寸下甚至超過了10%；近似公式形式簡單，缺點是準確度低。有限元軟件能以較高的準確度求解復雜工程電磁問題，但是需要使用者能熟練、正確地使用軟件。

[1]Marcuvitz N.Waveguide handbook[M].New York:Mcgraw-Hill,1951.

[2]Ramo S,Whinnery J R.Fields and waves in modern radio[M].New York:John Wiley &Sons,1953.

[3]Whinnery J R,Jamieson H W.Equivalent circuits for discontinuities in transmission lines[J].Proceedings of the IRE,1944,32(2):98-114.

[4]Whinnery J R,Jamieson H W,Robbins T E.Coaxial-line discontinuities[J].Proceedings of the IRE,1944,32(11):695-709.

[5]胡榕,崔翔,陳維江,等.特高壓氣體絕緣開關設備瞬態外殼電壓特性的試驗研究[J].中國電機工程學報,2014,34(29):5244-5258.Hu Rong,Cui Xiang,Chen Weijiang,et al.Experimental research on the characteristics of transient enclosure voltage in ultra high voltage gas insulated switchgear[J].Proceedings of the CSEE,2014,34(29):5244-5258.

[6]吳昊,李成榕,徐海瑞,等.用于VFTO 測量的GIS窗口式傳感器[J].電工技術學報,2012,27(9):210-217.Wu Hao,Li Chengrong,Xu Hairui,et al.Method for measurement of VFTO based on GIS disk sensor[J].Transactions of China Electrotechnical Society,2012,27(9):210-217.

[7]孟濤,林莘,徐建源.分段電弧模型下VFTO 的計算與分析[J].電工技術學報,2010,25(9):69-73.Meng Tao,Lin Xin,Xu Jianyuan.Calculation of very fast transient over-voltage on the condition of segmental arcing model[J].Transactions of China Electrotechnical Society,2010,25(9):69-73.

[8]倪光正.工程電磁場原理[M].2 版.北京:高等教育出版社,2009.

[9]Harrington R F.Time-harmonic electromagnetic Fields[M].New York:Wiley-IEEE Press,2001.

[10]張善杰.矢量函數、圓柱函數和球函數[M].南京:南京大學出版社,2011.

[11]王澤忠,全玉生,盧斌先.工程電磁場[M].北京:清華大學出版社,2004.

[12]王竹溪,郭敦仁.特殊函數概論[M].北京:北京大學出版社,2012.

[13]胡仁喜,孫明禮.ANSYS13.0 電磁學有限元分析從入門到精通[M].北京:機械工業出版社,2011.

[14]龍非池,王慧.基于 Schwarz-Christoffel 變換的平板電容器電場電荷分布仿真[J].物理與工程,2007,17(6):25-27.Long Feichi,Wang Hui.Simulation on the distribution of electric field and charges of flat capacitor based on schwarz-christoffel transformation[J].Physics and Engineering,2007,17(6):25-27.

[15]吳文輝,曹祥麟.電力系統電磁暫態計算與 EMTP應用[M].北京:中國水利水電出版社,2012.

[16]楊琳,吳廣寧,田曉菲.基于EMTP 的水平接地體沖擊時-頻特性分析[J].電工技術學報,2011,26(6):194-198.Yang Lin,Wu Guangning,Tian Xiaofei.Analysis of impulse characteristic grounding electrode in frequency and time domain based on EMTP[J].Transactions of China Electrotechnical Society,2011,26(6):194-198.