“幾何直觀”在小學數學教學中的運用

黃艷

《義務教育數學課程標準》指出：“幾何直觀主要是指利用圖形描述和分析問題.”數學教師進行授課過程中，由于小學生自身特點決定，其思維模式單一，具有一定的局限性，且知識儲備有限，因此，教學環節往往會出現某些困難或障礙.幾何直觀具有形象性強的特性，能幫助學生有效理解數學知識點.因此，運用幾何直觀可以實現輕松學習數學知識的目的.具體可從以下三方面著手：

一、對概念的理解更加清晰

小學生對于數學概念的理解和掌握具有一定的困難，這往往是數學概念自身的抽象性和邏輯性造成的.為此，數學教師在進行授課環節時，可利用幾何直觀，化抽象概念為具體，減少學生在理解上的難度，進而輕松、深刻地理解數學概念.下面以《面積的意義和面積單位》的教學片斷為例，進行說明：

師：在之前課程的學習中我們已經有效了解了線段的含義、長方形的概念、正方形的特征，那么，接下來同學們仔細觀察以上幾幅圖形（教師運用多媒體向學生展示兩片形狀各異的樹葉圖片），并向大家闡述自己的觀點與感受.

生：第一片樹葉較小，第二片樹葉則很大.

師：接下來向學生展示兩個正方形，讓學生談談這兩個正方形各自的特點.

生：兩個正方形的大小不同.

師：回答得非常不錯！同學們，無論是樹葉，還是正方形、黑板、書本等等我們都可以將它們統一稱作物體.那么用來表示這些物體的表面大小的概念就是——面積.大家自己思考一下，我們如何才能精準地判斷兩個不同物體的大小呢？

生：可以用眼睛觀察.

生：可把物體分成若干小方格，方格數量越多，圖形的面積就越大.

師：用方格子的方法可取嗎？同學們，請你們看看上面這幾幅圖形.通過這幾個圖形的格子數量我們是不是就可以知道這些圖形哪個比較大，哪個比較小呢？

生：這種方法是錯誤的，因為每個格子的大小不同，所以沒辦法進行合理比較.

師：好，同學們說得非常好，換句話說，也就是我們要想精準地得到圖形的面積，就應該使用大小統一的方格，在這里，大小統一的方格也就是大小相等的方格.由此，我們可以準確理解國際上對于面積單位的定義，即為一定標準的正方形的面積大小.

作為數學教師應該懂得，數學是一個逐步構建思維體系的過程，在思維體系的構建中，只有不斷從中進行體驗和思考，才能在其中發現美妙的風景，并得到有效的感悟和體會，進而了解抽象的數學概念，建立穩固的熟悉思維體系.在上述教學環節的再現過程中，我們可以得知，數學教師在通過幾何圖形進行數學概念的講解中，學生就可以更為直觀地進行理解和掌握，進而輕松感受到面積的含義和面積單位的形成過程.

二、對規律的掌握更加直觀

數學學科是小學科目中邏輯性最強且難度最大的學科，每個知識點之間都具有密切的聯系.因此，教師在進行數學科目的教學過程中，可以根據其知識點間的聯系入手，從其固有的聯系中著手，給學生創設一定的數學教學情境，進而實現舉一反三，活學活用的教學效果.下面以《三角形的三邊關系》教學片斷為例：

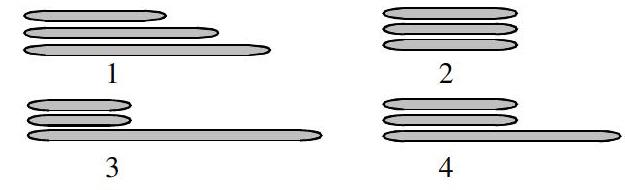
師：同學們，下面老師為大家準備幾組長度不同的小棒，請大家仔細觀察，動手操作，看看哪一組小棒能夠圍成三角形，并在旁邊打上對號.

1. （3，4，5） 2. （3，3，3） 3. （2，2，6） 4. （3，3，5）

生：第一組小棒能圍成一個三角形.

生：第二組小棒也能圍成一個三角形.

生：第三組小棒不能圍成三角形.

師：同學們，你們是怎么樣得出這個結論來的呢？請把這個過程告訴老師，也和大家一起分享一下.

生：我用第二組小棒動手進行搭建的時候，發現2 cm的邊長太短了，不能圍成一個三角形.

師：同學們回答的非常好，也就是說，你們剛才所得出的結論是通過自己動手操作得來的，那么在操作的過程中，同學們關于組成三角形的條件你們領悟到了什么或者明白了什么道理？

生：要想組成三角形，必須要使三角形的其中任何兩條邊大于或者等于第三條邊才可以.

通過利用幾何圖形進行三角形和其三邊規律的講解，教師不僅可以鍛煉學生的動手操作能力，也可以有效引導學生進行積極思考，在頭腦中加深印象，使學生對于三角形及其三邊規律有更為形象的認識，以便加深理解和記憶.

三、對問題的解決更加輕松

在某些數學問題中，其已知條件相對復雜，對于小學生來說理解有些困難，如果僅憑教師的口頭講授則過于簡練，不利于學生的消化理解，若在此過程中教師可以借助幾何圖形來解決，那么問題解決將會更加輕松，達到事半功倍的效果.

總之，教師在進行教學活動中，應敢于放手，利用幾何直觀方式將復雜的數學難題具體化、直觀化，尋找最為簡便的解題辦法，提高學生的數學思維，進而有效探索數學規律，達到巧妙學習數學的目的.