淺談面積法在幾何證明中的應用

楊敏欣

（福建省惠安第五中學）

淺談面積法在幾何證明中的應用

楊敏欣

（福建省惠安第五中學）

在初中幾何題中，經常會碰到一些和垂線段有關的問題，這就要求學生要懂得利用特殊位置法猜測垂線段之間的數量關系，善于構造三角形并利用三角形面積之間的數量關系證明結論。

面積法；垂線段；等邊三角形；幾何證明

探究內容：

①探究直角三角形三邊與斜邊上的高的數量關系。

②如圖2，等腰△ABC中，AB=AC，P是底邊BC上一動點P到兩腰的距離分別為PE、PF，PE+PF是一個定值嗎？該定值會等于誰？證明你的猜想。

如果P點在BC或CB的延長線上，你又能得到什么結論?

把等腰三角形改成等腰梯形，還有同樣的結論嗎？

③如圖3，在矩形ABCD中，P是AB上一動點，PE⊥AC于E，PF⊥BD于F，PE+PF是一個定值嗎？本探究題和探究②有聯系嗎？

④如圖4，等邊△ABC中，P是三角形內任意一點P到三邊的距離分別為PD、PE、PF，PD+PE+PF是定值嗎？該定值會等于誰？證明你的猜想。當P點在等邊三角形ABC外部時,上述的和還會是定值嗎？

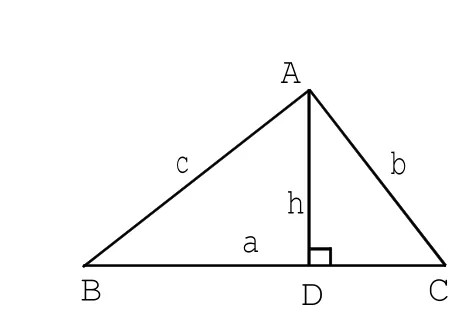
圖1

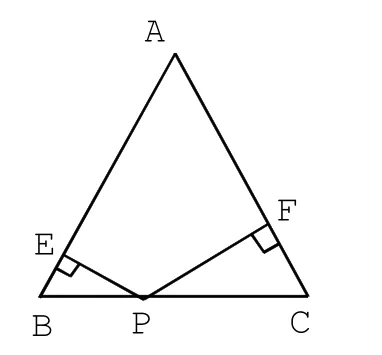
圖2

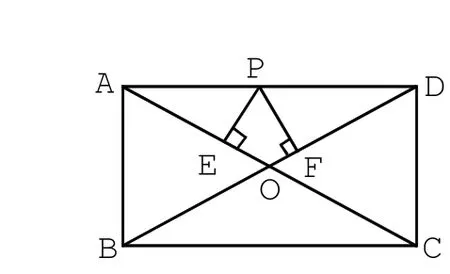
圖3

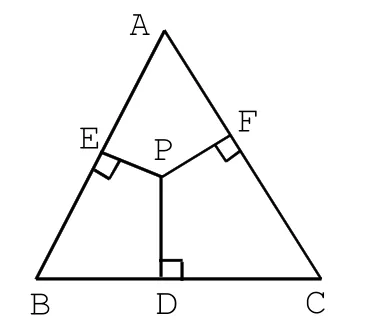
圖4

如果P點在△ABC外，你又能得到什么結論？

探究①：如圖1，設AB=c，BC=a，AC=b，AD=h，由三角形面積可得S△ABC=bc=ah，∴h=。

探究②：（1）如圖2，當P點在線段BC上，設h為△ABC中BC邊上的高。

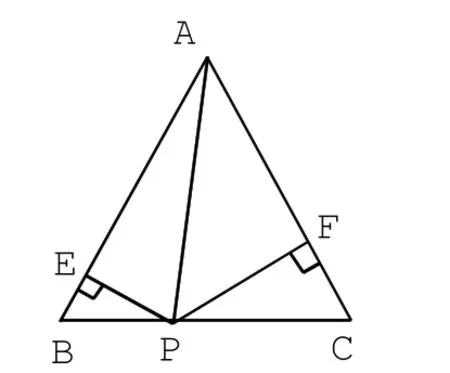
圖2 -1

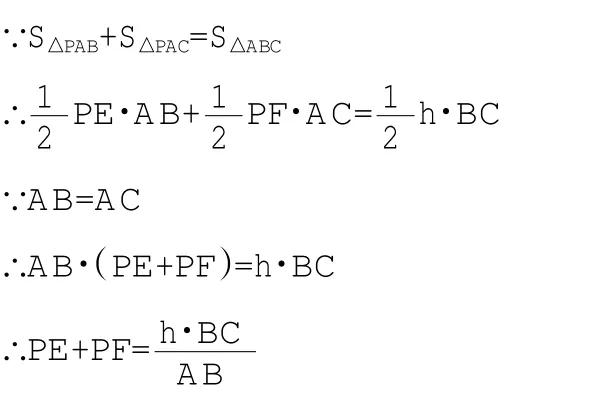
因而可得PE+PF的和是一個定值。

（2）如圖2-2，當P點在線段CB的延長線上，設h為△ABC中BC邊上的高，連接AP

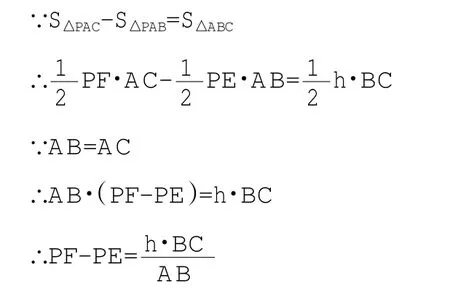
因而PF-PE的差是一個定值。

同理可證，當P點在BC的延長線上，PE-PF的差也是一個定值，為

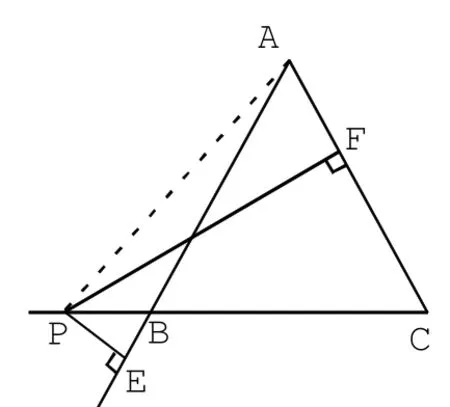
圖2 -2

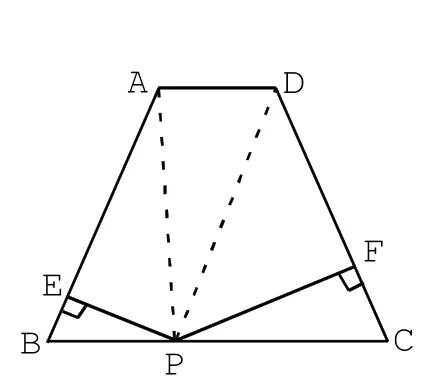
圖2 -3

當把等腰三角形改為等腰梯形時，

（1）如圖2-3，當動點P在BC線段上運動，連接AP和DP，設h為等腰梯形ABCD的高，

（2）如圖2-4所示，當動點P在BC線段的延長線上運動時，連接AP和DP

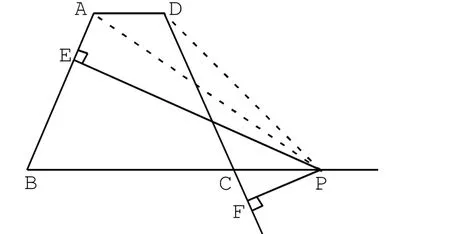
圖2 -4

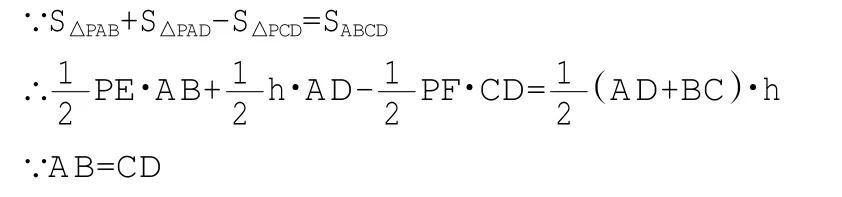
同理可證，P點在CB的延長線上，PF-PE的差也是一個定值，PE-PF=

結論：當把等腰三角形改為等腰梯形時，動點P在線段BC上運動時，PE+PF的和是一個定值，為；當動點P在BC或 CB的延長線上為定值。

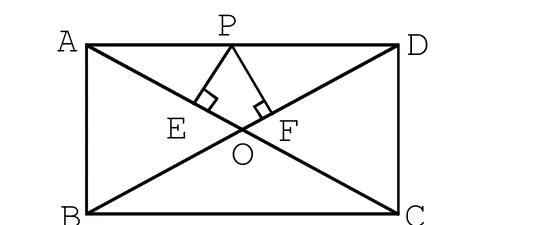
圖3

探究④：（1）如圖4-1，當P點在三角形ABC內部時，連接AP和BP，CP

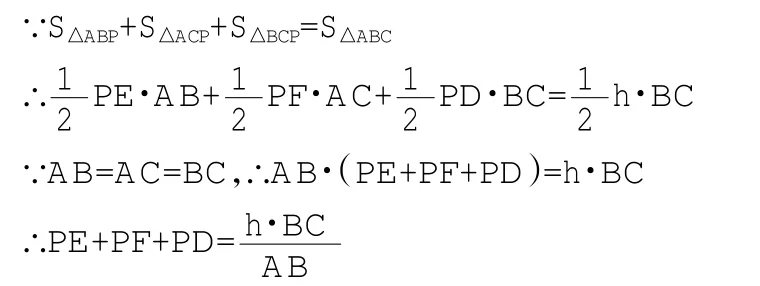
故PE+PF+PD的和為定值。

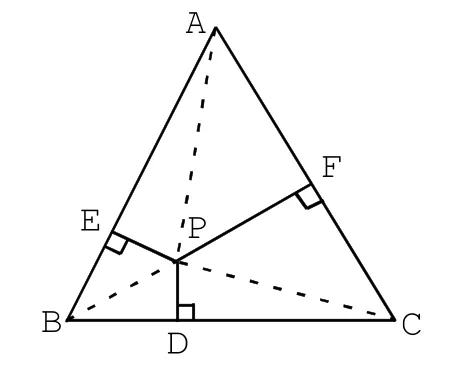
圖4 -1

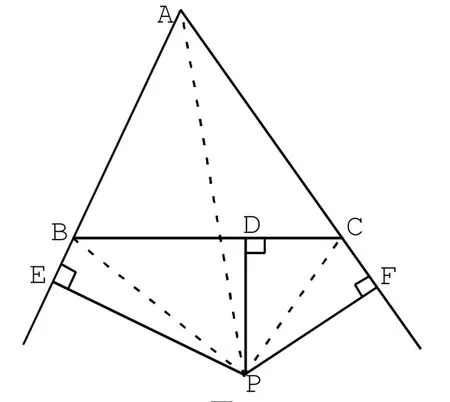
圖4 -2

（2）如圖4-2，當P點在三角形ABC外部時，連接AP和BP，CP

故PE+PF-PD的值為定值。

［1］朱德祥，朱維宗.初等幾何研究［M］.高等教育出版社，2003.

［2］余昌紅.淺談等面積法在幾何題中的應用［J］.新課程導學，2011（13）.

·編輯 謝尾合