在具體問題中學習條件概率
林潔
(廣東佛山南海區九江中學)
在具體問題中學習條件概率
林潔
(廣東佛山南海區九江中學)
條件概率是新課標高考的考查內容,理解和計算的難度不大,但是許多同學一遇到題目中有“條件”的概率對題目就糊涂了,區分不清這個“條件”只是題目的已知,還是因此條件這個題目就是“條件概率”了?其實,條件概率并非想象中的那樣難理解,以下用具體題目的分析,來幫助我們發現“條件”的意義所在。
首先,要理解條件概率的定義,即:在事件A已經發生的條件下,事件B發生的概率,稱為事件B在給定A下的條件概率,
【實例分析1】甲、乙2人各進行一次射擊,如果2人擊中目標的概率都是0.6,且相互之間沒有影響,計算:
(1)2人都擊中目標的概率;
(2)甲擊中目標的條件下,乙擊中目標的概率;
(1)甲、乙擊中目標,題目意在相互獨立事件同時發生的概率,即。
(2)甲擊中目標是條件,是必然發生事件,即A事件發生的前提下計算概率為。
對比發現兩個題目的區別:題目(1)中的甲可能擊中目標,也可能未擊中目標,我們只是計算甲、乙同時擊中目標的概率;題(2)中的甲則必須是擊中目標的,即甲擊中目標是必然事件,發生概率為1。
解:設甲擊中目標為事件A,乙擊中目標為事件B;
(1)甲乙2人都擊中目標的概率為P(AB)=P(A)·P(B)=0.6×0.6= 0.36;
(2)解法一:公式法:甲擊中目標的條件下,乙擊中目標的概率為。
解法二:因為事件A為條件,即A事件為必然發生事件,P(A)= 1;B事件發生的概率為P(B)=0.6,則AB事件同時發生的概率P(AB)=P(A)·P(B)=1×0.6=0.6。
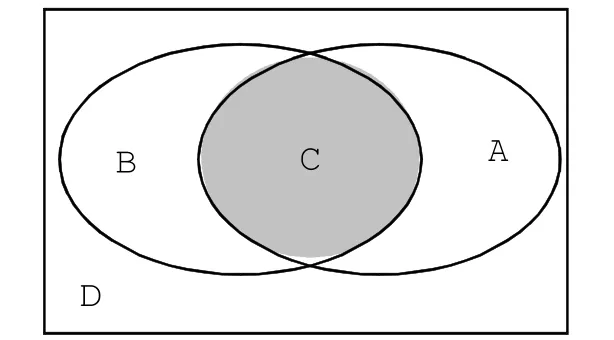
解法三:縮小樣本空間法,在“甲擊中目標”的條件下,計算乙擊中目標的概率為:
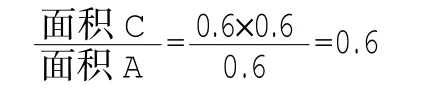
【實例分析2】袋中共有6個紅球和4個白球,每次抽取一個小球并且不放回,連續抽取2次,(1)求連續2次抽取的都是紅球的概率;
(2)求在第一次抽取紅球的條件下,第二次也抽取紅球的概率。
分析:連續抽取2次的所有情況如下:
①第一次是紅球,第二次也是紅球;
②第一次是白球,第二次也是白球;
③第一次是白球,第二次是紅球;
④第一次是紅球,第二次是白球。
(1)連續2次抽取紅球,題目意在相互獨立事件同時發生的概率;
(2)在第一次抽取紅球是條件,是個必然事件,那么題目中要求的第二次也抽到紅球其實就相當于袋中只有9球(5個紅球),求抽到紅球的概率,所以答案是。
對比發現兩個題目的區別:題目(1)中的第一次抽取可能是紅球,也可能是白球,我們只是計算2次都抽到紅球的概率;題(2)中的第一次抽取的則必須是紅球,即第一次抽到紅球的事件必然發生,其發生的概率為1。
解:設第一次抽到紅球的事件為A,第二次抽到紅球的事件為B
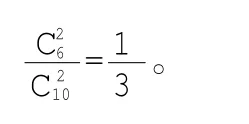
解法(二):第一次抽取是從10個球(有6個紅球)中抽,故
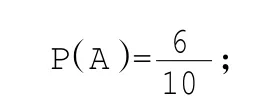
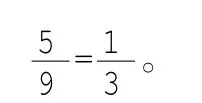
(2)解法(一):公式法,第一次抽取紅球的條件下,第二次也抽取紅球的概率為
解法(二):因為事件A為條件,即A事件為必然發生事件,P(A)=1;B事件發生的概率為P(B)=,則AB事件同時發生的概率為
解法(三):縮小樣本空間法,即“第一次抽到紅球”的條件發生后,計算在9個球(含5個紅球)中抽到紅球的概率為
以上題目我們可以對比歸納出,判斷是否符合條件概率的標準是:“條件”是不是一定要發生,如果“條件”不是一定發生的,則不是條件概率;如果“條件”一定發生,則滿足條件概率,計算的方法有三種:(1)公式法,即;(2)利用“條件P(A)=1”,只需計算兩個事件同時發生,即P(AB)= P(A)·P(B);(3)縮小樣本空間法,即在“條件”發生后的樣本空間內計算概率,此法相對更容易理解,計算更加簡單。
此考點一般以客觀題考查,或者在主觀題中的第一問,難度不高,同學們針對此考點一定要將訓練的重點放在“條件”的“識別”上,牢記一個標準“一定發生的才是條件”。明確方向,細心計算,考點得分將不是問題。
·編輯 謝尾合

