動(dòng)中感悟，水到渠成

陳銘河

[摘 要] 三角形內(nèi)角和是三角形的一個(gè)重要性質(zhì). 新課程要求遵循學(xué)生學(xué)習(xí)數(shù)學(xué)的心理規(guī)律，強(qiáng)調(diào)從學(xué)生已有的生活經(jīng)驗(yàn)出發(fā)，讓學(xué)生親身經(jīng)歷將實(shí)際的問題抽象成數(shù)學(xué)的知識(shí). 《三角形的內(nèi)角》這一課意在讓學(xué)生主動(dòng)地參與數(shù)學(xué)活動(dòng)，并通過(guò)親手“實(shí)驗(yàn)—剪拼”，從而在大腦里“猜想—發(fā)現(xiàn)—?jiǎng)?chuàng)造”. 通過(guò)教學(xué)方式的改變來(lái)促使學(xué)生學(xué)習(xí)方式的轉(zhuǎn)變，盤活學(xué)生思維，從而更好地促進(jìn)學(xué)生主體的發(fā)展.

[關(guān)鍵詞] 內(nèi)角和；探究；思維

根據(jù)新課標(biāo)理念，初中“空間與圖形”的教學(xué)，應(yīng)體現(xiàn)經(jīng)歷觀察、實(shí)驗(yàn)、猜想、證明等數(shù)學(xué)活動(dòng)過(guò)程，發(fā)展合情推理能力和初步的演繹推理能力，能合理、清晰地闡述自己的觀點(diǎn)，形成解決問題的一些基本策略，體驗(yàn)解決問題策略的多樣性，對(duì)數(shù)學(xué)產(chǎn)生好奇心和求知欲，發(fā)展實(shí)踐能力和創(chuàng)新精神，鍛煉學(xué)生克服困難的意志，建立自信心，并獲得成功的體驗(yàn).

教學(xué)時(shí)，教師應(yīng)切實(shí)踐行新課標(biāo)理念，以教者有意、學(xué)者無(wú)意的方式滲透數(shù)學(xué)思想和方法，打開學(xué)生思維的閘門，大膽猜測(cè)，合理推證，發(fā)展學(xué)生思維的靈活性、廣闊性、創(chuàng)造性. 結(jié)合新人教版八年級(jí)上冊(cè)《11.2.1？搖三角形的內(nèi)角》一節(jié)談?wù)勛约旱慕虒W(xué)所感.

吃透教材是起點(diǎn)

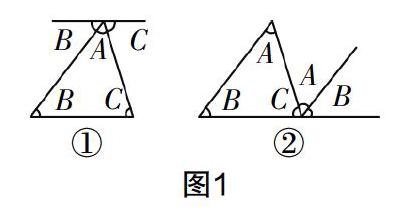
本節(jié)課的主要內(nèi)容是探索、證明、運(yùn)用三角形內(nèi)角和定理. 三角形內(nèi)角和定理是任意三角形的一個(gè)重要性質(zhì)，在理論和實(shí)踐中應(yīng)用非常廣泛. 這個(gè)定理證明的難點(diǎn)是如何添加輔助線，這就要求教師要吃透教材的編寫意圖，處理好教材. 與學(xué)生一道從動(dòng)手實(shí)驗(yàn)入手. 如圖1所示那樣. 通過(guò)拼合等方法來(lái)突破此難點(diǎn)，慢慢地、細(xì)致地引導(dǎo)學(xué)生把實(shí)驗(yàn)的結(jié)果抽象為幾何語(yǔ)言，并從中得出輔助線的添加方法，讓輔助線的出現(xiàn)水到渠成.

教材中的探究語(yǔ)言，學(xué)生也感覺模糊，如教材“探究：在紙上畫一個(gè)三角形，并將它的內(nèi)角剪下拼合在一起，就得到一個(gè)平角”. 教材的表述是“在圖1①中，將∠B和∠C分別拼在∠A的左右兩邊，三個(gè)角合起來(lái)形成一個(gè)平角”. 教學(xué)此處時(shí)，學(xué)生就會(huì)發(fā)問：將∠B和∠C分別拼在∠A的左右兩邊，三個(gè)角合起來(lái)為什么會(huì)形成一個(gè)平角？學(xué)生的問題提得多么經(jīng)典，抓住了要害. 事實(shí)上，現(xiàn)在要初一的學(xué)生來(lái)證明是平角是有難度的，但問題已擺出來(lái)，就一定要讓學(xué)生明白其中的道理. 實(shí)際上原因是這樣的：在圖1①中，將∠B和∠C分別拼在∠A的左右兩邊，就分別構(gòu)成了內(nèi)錯(cuò)角. 由內(nèi)錯(cuò)角相等可得，拼接后的∠B的一條邊平行于BC；同理，拼接后的∠C的一條邊也平行于BC，由“經(jīng)過(guò)直線外一點(diǎn)，有且只有一條直線與這條直線平行”可得，拼接后的∠B的一條邊與拼接后的∠C的一條邊在同一條直線上，并且這條直線平行于邊BC. 教材為了降低難度，在證明中就避開了這一點(diǎn)，而是寫成“過(guò)點(diǎn)A作直線l，使l∥BC”，這就將實(shí)驗(yàn)結(jié)論與理論證明有機(jī)地整合在一起. 故此，教師把教材吃透了，教學(xué)時(shí)才能猶如庖丁解牛，必然游刃有余.

探究展現(xiàn)是關(guān)鍵點(diǎn)

新課標(biāo)明確說(shuō)明：認(rèn)識(shí)通過(guò)觀察、實(shí)驗(yàn)、歸納、類比、推斷可以獲得數(shù)學(xué)猜想，體驗(yàn)數(shù)學(xué)活動(dòng)充滿著探索性和創(chuàng)造性，感受證明的必要性、證明過(guò)程的嚴(yán)謹(jǐn)性以及結(jié)論的確定性. 這個(gè)觀點(diǎn)對(duì)于《三角形的內(nèi)角》的教學(xué)具有很大的理論指導(dǎo)意義，因?yàn)檫@個(gè)定理的證明難點(diǎn)是如何添加輔助線，對(duì)初一學(xué)生來(lái)說(shuō)是“抹布洗臉——初相識(shí)”. 為了讓輔助線走進(jìn)學(xué)生的頭腦，貼近學(xué)生的幾何學(xué)習(xí)，筆者采用了以下教法與學(xué)生一同探討，使學(xué)生在大腦里形成“實(shí)驗(yàn)—猜想—發(fā)現(xiàn)—?jiǎng)?chuàng)造”的思維模型.

環(huán)節(jié)一：筆者先將學(xué)生分成2人一組，每組準(zhǔn)備好三角形紙片.

環(huán)節(jié)二：以小組為單位進(jìn)行“實(shí)驗(yàn)—剪拼—猜想—發(fā)現(xiàn)—?jiǎng)?chuàng)造”，并將三個(gè)啟發(fā)思維的問題用多媒體展示：（1）有多少種方法可以拼此結(jié)論？（2）所拼出的圖，能用以前學(xué)過(guò)的哪些知識(shí)來(lái)說(shuō)明此結(jié)論？（3）你能根據(jù)拼圖引發(fā)出一種輔助線嗎？

環(huán)節(jié)三：成果展示. 由各組將拼出的圖貼在黑板上，并推薦一個(gè)成員進(jìn)行解說(shuō).

環(huán)節(jié)四：以小組為單位對(duì)各組的合作學(xué)習(xí)情況進(jìn)行評(píng)價(jià).

環(huán)節(jié)五：動(dòng)態(tài)再現(xiàn)，激活思維. 筆者將制作的動(dòng)片通過(guò)多媒體規(guī)范再現(xiàn)給學(xué)生，讓學(xué)生對(duì)比感悟、發(fā)現(xiàn)不同的論證方法.

環(huán)節(jié)六：明確輔助線的表述，這是本節(jié)課的難點(diǎn)，也是后續(xù)學(xué)習(xí)幾何的支點(diǎn). 筆者通過(guò)多媒體課件的動(dòng)態(tài)展示，讓學(xué)生憑借直覺，再次動(dòng)中感悟，引領(lǐng)學(xué)生發(fā)現(xiàn)主要有以下幾種常用添畫輔助線的方法推證定理：

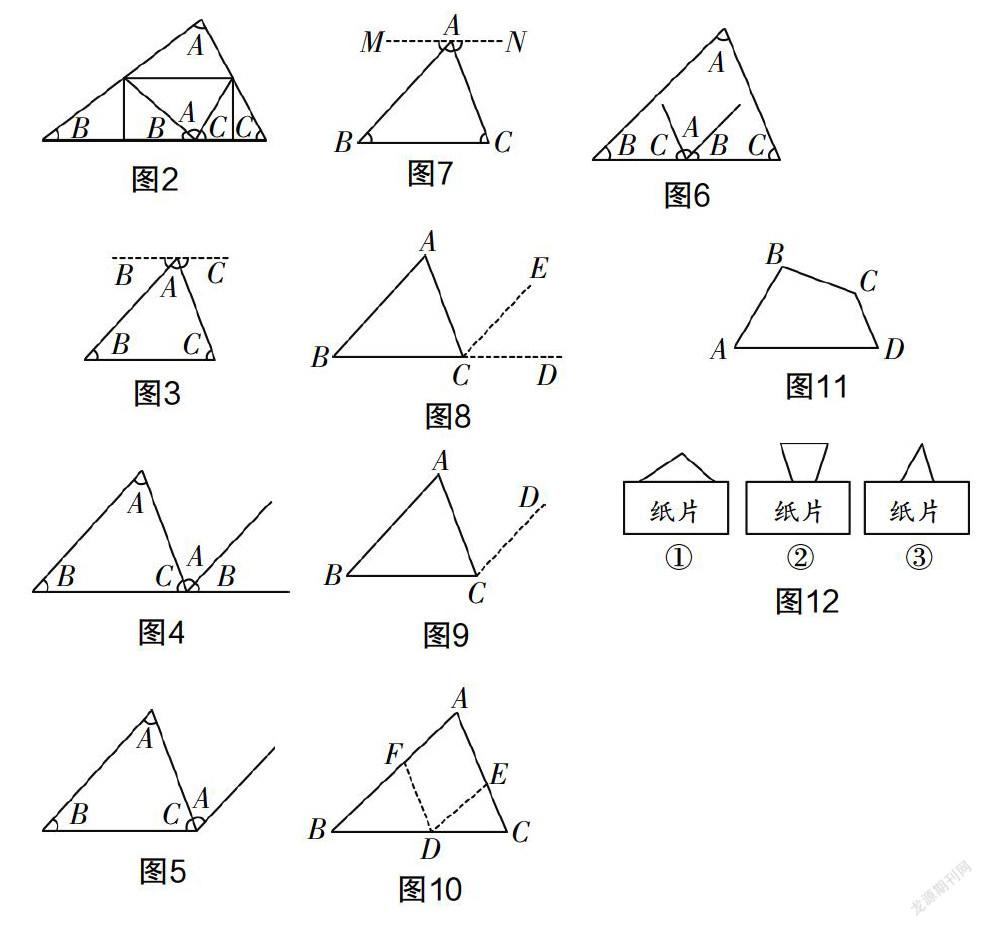
方法一：如圖7，過(guò)點(diǎn)A作MN∥BC.

方法二：如圖8， 延長(zhǎng)BC，過(guò)點(diǎn)C作CE∥BA.

方法三：如圖9，過(guò)點(diǎn)C作CD∥BA.

方法四：如圖10，在BC邊上任取點(diǎn)D（不與點(diǎn)B，C重合），過(guò)點(diǎn)D作DE∥BA交AC于點(diǎn)E，DF∥CA交AB于點(diǎn)F.

鑒于學(xué)生初學(xué)，知識(shí)水平所限，以上幾種方法要求每個(gè)學(xué)生至少掌握一種，這里拋給優(yōu)生一個(gè)問題：“證明此定理，遠(yuǎn)不止以上四種方法，課外再去討論，歡迎隨時(shí)來(lái)辦公室與我交流. ”等學(xué)生學(xué)一段時(shí)間后，學(xué)生水平進(jìn)一步提高，再“殺回馬槍”，開展一次活動(dòng)交流課，可以啟發(fā)學(xué)生聯(lián)想：過(guò)三角形一個(gè)頂點(diǎn)作對(duì)邊的平行線；過(guò)三角形各邊上任意一點(diǎn)（非頂點(diǎn)），分別作另兩邊的平行線；過(guò)三角形內(nèi)或外任意一點(diǎn)，分別作三邊的平行線；過(guò)三角形三個(gè)頂點(diǎn)作一組互相平行的平行線……這樣就有幾十種添畫輔助線的方法，多角度、多側(cè)面激勵(lì)學(xué)生探究數(shù)學(xué)的無(wú)窮的奧妙，并逐步形成對(duì)較復(fù)雜圖形的觀察能力、辨別能力和處理能力. 不在于題海戰(zhàn)術(shù)，而在于融會(huì)貫通，將學(xué)生思維盤活，將冰冷的美麗轉(zhuǎn)化為火熱的發(fā)現(xiàn)，“隨風(fēng)潛入夜，潤(rùn)物細(xì)無(wú)聲”.

務(wù)實(shí)應(yīng)用是落腳點(diǎn)

學(xué)生學(xué)數(shù)學(xué)的目的不是為了做題，而是為了用數(shù)學(xué)思想、數(shù)學(xué)思維、數(shù)學(xué)方法去創(chuàng)造性地解決日常生活中大量的實(shí)際問題，學(xué)生會(huì)將實(shí)際問題轉(zhuǎn)化為數(shù)學(xué)問題，培養(yǎng)學(xué)生數(shù)學(xué)建模.

教學(xué)時(shí)，除了設(shè)計(jì)一些常規(guī)性的題之外，更應(yīng)設(shè)計(jì)一些開放性的題.

開放性試題1：某工廠生產(chǎn)一種模版如圖11，設(shè)計(jì)要求AB與DC相交成20°角，BC與AD相交成10°角.假如廠長(zhǎng)請(qǐng)你去當(dāng)質(zhì)檢員，你怎樣通過(guò)測(cè)量∠A，∠B，∠C，∠D的度數(shù)，來(lái)檢查模版是否為合格產(chǎn)品？

開放性試題2：如圖12，①、②、③各有一個(gè)三角形玻璃片，只露出了一部分，其余部分被紙片遮住，你能判斷它們各是什么三角形嗎？請(qǐng)談?wù)勀愕呐袛嗬碛?

教有法，但無(wú)定法，尤其是新課標(biāo)所體現(xiàn)的新理念，給教師提出了挑戰(zhàn)，給學(xué)生帶來(lái)了創(chuàng)造. 教學(xué)通過(guò)操作互動(dòng)，為學(xué)生探究問題創(chuàng)設(shè)輕松、愉快、平等的學(xué)習(xí)氛圍及創(chuàng)設(shè)生成的空間，善于設(shè)置符合學(xué)生認(rèn)知規(guī)律的學(xué)習(xí)情景，以此激發(fā)學(xué)生的探究欲望并行動(dòng)，這就要求教師以教材為載體，創(chuàng)造性教學(xué)，學(xué)生思維的靈活性、廣闊性、創(chuàng)造性等品質(zhì)才能得到充分發(fā)展，學(xué)生就能沿著開放的探索路風(fēng)雨無(wú)阻、大踏步前行.