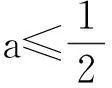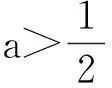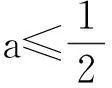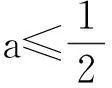“轉換”策略在課標卷把關題中的應用探析*

福建省漳州市第一中學　(363000)　劉開富　林新建

?

“轉換”策略在課標卷把關題中的應用探析*

福建省漳州市第一中學(363000)劉開富林新建

解題需要套路，看到一道題，你的第一反應是什么？迅速生成常規方案，也即第一方案.

為什么要有套路？因為80%的高考題是基本的、穩定的，考查運算的敏捷性.沒有套路，就沒有速度.比如，如何求函數的單調區間、證明函數的單調性；涉及參數問題時，把參數分離出來，轉化為這個參數與一個式子的不等或者相等關系；數列問題，設法轉化為基本數列(等差數列或等比數列)模型；解析幾何問題，根據條件特征選擇適當的算法：坐標、向量和運用幾何性質推演；概率計算，把一事件轉化為互斥事件的和或獨立事件的積，合理選用基本模型和分布；…等等.

問題是，當實施第一方案(套路)遇到障礙時，我們的策略是什么？

轉換視角，生成第二方案.轉換視角，轉換到哪里？轉換到知識豐富領域，也就是說把問題轉換到我們最熟悉的領域.

處理數學難題，從方法論的角度講就是轉換視角.常態方案不行，換一個方案行了；這種說法與思路不通，換一個說法通了；在一個領域內繁復的問題，換一個領域簡單了.

如若不是這樣，靠什么考查能力？又憑什么說高考是一種選拔性考試呢？

所謂試題的創新，本質上是視角的轉換，我們的解題就是要用創新應對創新，用轉換適應轉換.

1．條件轉換

對問題的某個條件作轉換，如式的恒等變形，語意的等價轉換等，這種轉換的目的是使問題簡單化、熟悉化.

例1(2010年高考新課標卷Ⅰ文科21題)

設函數f(x)=x(ex-1)-ax2.

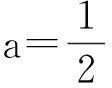
(Ⅱ)若當x≥0時f(x)≥0，求a的取值范圍.

解析：第(Ⅰ)問不難.

第(Ⅱ)問，f(x)=x(ex-1-ax)，令g(x)=ex-1-ax，則g′(x)=ex-a.

若a≤1，則當x∈(0,+∞)時，g′(x)>0，g(x)為增函數，而g(0)=0，從而當x≥0時g(x)≥0，即f(x)≥0.

若a>1，則當x∈(0,lna)時，g′(x)<0，g(x)為減函數，而g(0)=0，從而當x∈(0,lna)時g(x)<0，即f(x)<0.

綜合得a的取值范圍為(-∞,1].

評析：本題第(Ⅱ)問直接求解很難，我們通過將f(x)=x(ex-1)-ax2化為f(x)=x(ex-1-ax)，因為x≥0，所以條件“當x≥0時f(x)≥0”可轉換為“當x≥0時，g(x)=ex-1-ax≥0”.這樣一轉換，問題變得簡單易解，凸顯了“轉換策略”在求解數學難題中的重要作用.

例2(2007年高考全國卷Ⅱ理科22題)

已知函數f(x)=x3-x.

(Ⅰ)求曲線y=f(x)在點M(t,f(t))處的切線方程；

(Ⅱ)設a>0，如果過點(a,b)可作曲線y=f(x)的三條切線，證明：-a

解析：第(Ⅰ)問容易，求導得切線的斜率為k=3t2-1，進而由點斜式即得切線方程為y=(3t2-1)x-2t3.

難在第(Ⅱ)問，“過點(a,b)可作曲線y=f(x)的三條切線”，什么意思？如何下手？

如果我們把第(Ⅱ)問的條件換個說法，變為曲線y=f(x)的三條切線都過點(a,b)，也就是說存在三個t，使得直線y=(3t2-1)x-2t3過點(a,b)，或者說，關于t的三次方程b=(3t2-1)a-2t3有三個相異的實數根.

這么一轉換，問題可輕松獲解.令g(t)=2t3-3at2+a+b，則問題進一步轉換為曲線y=g(t)的圖像與t軸有三個交點.注意到三次函數只有兩種形態：一是沒有極值點，一是有兩個極值點.于是，這個三次函數的圖像應該是：先單調上升經過t軸達到極大值，再單調下降經過t軸達到極小值，而后單調上升第三次經過t軸.

這樣問題就歸結為[g(t)]極大>0，[g(t)]極小<0，進而由極大值g(0)=a+b>0，極小值g(a)=-a3+a+b=b-f(a)<0，問題得證.

評析：本題第(Ⅱ)問獲解的關鍵也是條件轉換，將“過點(a,b)可作曲線y=f(x)的三條切線”轉換為“曲線y=f(x)的三條切線都過點(a,b)”，使得問題變得清晰熟悉，易于求解.

2．結論轉換

對問題的結論作轉換，如恒等變形、等價轉化等，這種轉換的目的是使問題簡單化、明朗化.

例3(2014年高考新課標卷Ⅰ理科21題)

(Ⅰ)求a，b；(Ⅱ)證明： f(x)>1.

3．命題轉換

根據命題的等價性進行轉換等，這種“不同說法”之間的轉換常常可以使那些“理不清”或“說不清”的問題變得容易判斷、理解.

例4(2010年高考新課標卷Ⅰ理科21題)

設函數f(x)=ex-1-x-ax2.

(Ⅰ)若a=0，求f(x)的單調區間；

(Ⅱ)若當x≥0時f(x)≥0，求a的取值范圍.

解析：第(Ⅰ)問較易.

第(Ⅱ)問，自然的想法是分離參數.

當x≥0時f(x)≥0，即ex-1-x-ax2≥0，ax2≤ex-1-x(x≥0).

但我們發現，沿著這個思路，是不能繼續下去的.

再構造函數，令h(x)=ex(x-2)+x+2(x>0)，則h′(x)=(x-1)ex+1.

由于(h′(x))′=xex>0對x∈(0,+∞)恒成立，所以h′(x)在(0,+∞)上為增函數，又h′(0)=0，所以當x∈(0,+∞)時，h′(x)>0，從而知h(x)在(0,+∞)上為增函數.因為h(0)=0，所以當x∈(0,+∞)時，h(x)>0，從而當x∈(0,+∞)時，g′(x)>0，g(x)為(0,+∞)上的增函數，所以g(x)>g(0)，a≤g(0).

問題似乎解決了，可是g(0)無意義，忙碌了半天，徒勞而無功.

問題陷入了僵局，怎么辦？

我們將問題作個轉換，將“當x≥0時f(x)≥0”換個說法，變為“f(x)在[0,+∞)上的值非負”.

如此一來，不難就此猜想出a的取值范圍.

至此，我們可將待證命題轉換為如下命題予以證明：

因為轉換，我們將高考把關題進行得如此簡單！沒有轉換，我們做什么？

參考文獻

[1]吳建山,林新建.自主招生考試數學解題四意識[J].福建中學數學,2014，1-2,14-16.

[2]林新建.數學高考解題的“三化四策八關注”[M].廈門：廈門大學出版社.

*本文是“2015年漳州市基礎教育課程與教學研究課題”《國家命題背景下數學高考復習教學的因應策略研究》的研究成果.