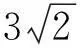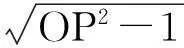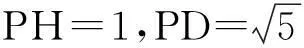以線段長為最值的試題的解法探究

浙江省臨海市東塍鎮中學　(317000)　潘優紅

?

以線段長為最值的試題的解法探究

浙江省臨海市東塍鎮中學(317000)潘優紅

實行新課程標準以來，各地中考以線段長最大(或小)值為載體的新編試題頻頻出現，在我們的日常教學中也常遇到此類問題.從我們的教學實踐中知道，學生對這類問題很不適應，往往難以入手，理不清解題思路，面對選擇題、填空題時，僅憑直覺去猜答案.其實，解這類問題的根本依據往往又是學生很熟悉的性質：兩點之間線段最短.或是另一種表達形式：三角形兩邊之和大于第三邊(或兩邊之差小于第三邊).學生往往忽略這一基本性質，或由于題目條件的隱蔽而找不到與這一性質的聯系造成思維受阻.“人教2013年版《義務教育課程標準實驗教科書·數學》八年級上冊”第85頁13.4課題學習《最短路徑問題》中的問題一(飲馬問題)與問題二(造橋選址問題)，提供了我們解這類問題的兩個很好的模型.下面我們對一些試題的解法根據教學實踐作一些整理與探究，供同行研討，供同學參考.

一、應用“飲馬問題”模型解題

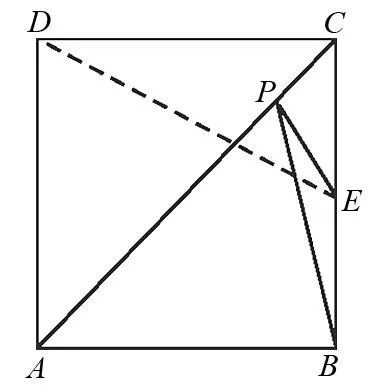
圖1

題1(2012年攀枝花中考題)如圖1，在正方形ABCD中，AB=4，E是BC的中點，點P是對角線AC上一動點，則PE+PB的最小值為.

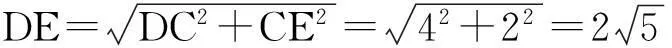
題2(2012年濱州中考題)如圖2，在平面直角坐標系中，拋物線y=ax2+bx+c經過A(-2，-4)，O(0，0)，B(2,0)三點.

(1)求拋物線y=ax2+bx+c的解析式；

(2)若點M是拋物線對稱軸上一點，求AM+OM的最小值.

圖2

二、應用“造橋選址問題”模型解題

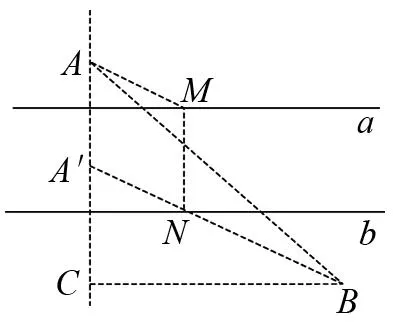
圖3

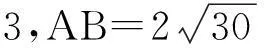
(A)6(B)8(C)10(D)12

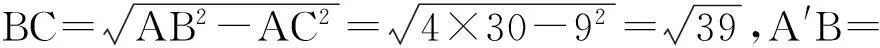
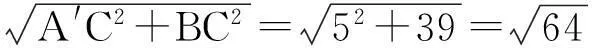
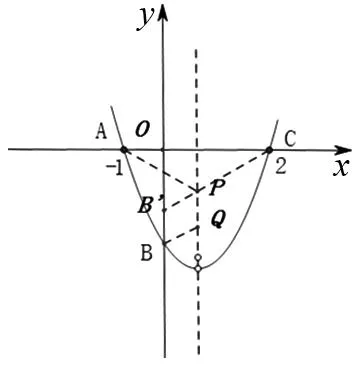
圖4

(1)求A、B、C三點的坐標；

(2)已知點D在坐標平面內，ΔABD是頂角為120°的等腰三角形，求點D的坐標；

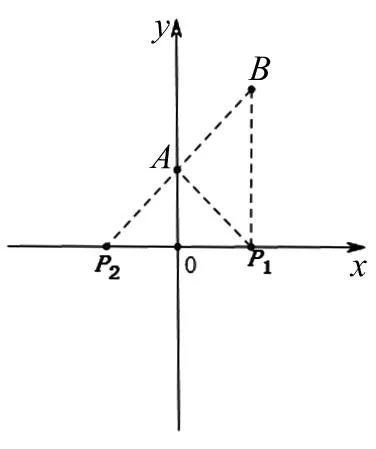
圖5

三、其他涉及線段長最值問題

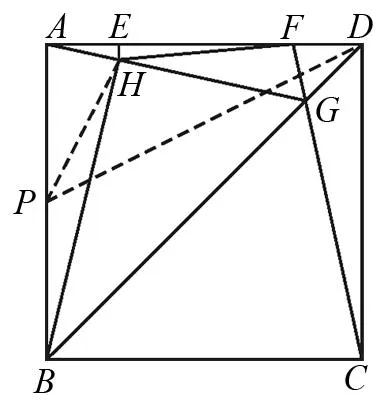
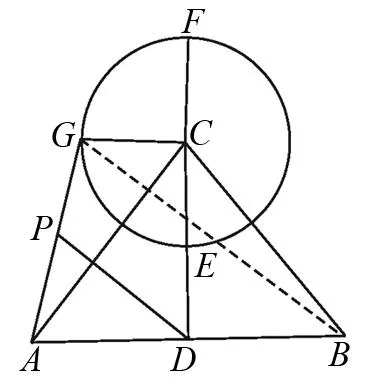
題5在平面直角坐標系xoy中，已知A(0，1),B(1，2 ).點P在x軸上運動，當點P到A、B兩點距離之差的絕對值最大時，點P的坐標是.

解法探究：解這類沒圖的題，首先要畫出示意圖，以直觀的形式提供我們解題思路.于是畫如圖5，再表述出點P到A、B兩點距離之差的絕對值|PB-PA|.怎樣找它的最大值呢？我們聯想到三角形兩邊之差小于第三邊，則有PB-PA

圖6

圖7

題7(2012年濟南中考題)如圖7，∠MON=90°，矩形ABCD的頂點A、B分別在邊OM、ON上，當B在邊ON上運動時，A隨之在邊OM上運動，矩形ABCD的形狀保持不變，其中AB=2，BC=1，運動過程中，點D到點O的最大距離為().

圖8

題8(2013年武漢中考題)如圖8，E,F是正方形ABCD的邊AD上兩個動點，滿足AE=DF，連接CF交BD于點G，連接BE交AG于點H，若正方形的邊長為2，則線段DH長度的最小值是.

解法探究：本題圖形比較復雜，DH的長似乎無規律可循.我們只好重新閱讀題目，從中找出隱含的條件.正方形隱含的邊相等、角相等且都是直角、關于直線BD對稱.現在這些對我們有用嗎？結合圖形及AE=DF，可得△ABE?△DCF、△ADG?△CDG，所以 ∠ABE=∠DCF=∠DAG，這時可以證明∠AHB=90°

圖9

題9(2015年杭州江干區中考模擬題)如圖9,CA=CB，AB=6，CD=4，E是高線CD的中點，以CE為半徑作⊙C，G是⊙C上一個動點，P是AG中點，則DP的最大值為().